5. Сепаратрисы

Первый интеграл уравнения фазовых колебаний

(6.20)

является гамильтонианом системы и может быть проанализирован, как это обычно делается в теории линейных ускорителей. Здесь и являются известными начальными условиями. Они не обязательно должны выбираться в начале процесса (т.е. при ), а могут быть взяты при любом промежуточном моменте процесса, описываемого дифференциальным уравнением. Возьмем случай, когда энергия частиц в синхротроне меньше критической. Как мы знаем из анализа автофазировки в линейных ускорителях, фаза есть левый предел области устойчивости фазовых колебаний. Если фаза частицы при ее движении влево доходит до точки , то частицы здесь останавливается и дальнейшее движение по фазе продолжается только после этой остановки. Следовательно, «начальному» значению соответствует «начальное» значение . В результате для этих начальных условий для (6.20) получаем

. (6.21)

Отсюда сразу видно, что обе границы области устойчивости фазовых колебаний соответствуют условию ; левая граница очевидна , правая граница получается из решения уравнения

.

Фазовым синхротронным колебаниям соответствуют синхротронные колебания энергии неравновесной частицы около энергии равновесной частицы. Связь колебаний энергии с колебаниями фазы описывается уравнением (6.15), из которого видно, что колебания фазы и энергии неравновесной частицы сдвинуты по фазе на (в масштабе синхротронных колебаний), так как согласно (6.15) имеем . Следовательно, в момент, когда скорость изменения фазы максимальна (т.е. когда текущая фаза неравновесной частицы принимает значение ), энергия этой частицы максимально отличается от энергии равновесной частицы. Когда же фаза неравновесной частицы останавливается на максимальном расстоянии от слева и справа (т.е. в момент когда ), энергия неравновесной частицы сравнивается с энергией равновесной частицы ( ).

Выражение (6.21) представляет собой уравнение сепаратрисы, поскольку этому выражению удовлетворяет точка и . Уравнение (6.21) определяет контур сепаратрисы в плоскости переменных и . В выражение (6.21) входит параметр , следовательно, оно задает семейство сепаратрис, каждая из которых соответствует определенному значению равновесной фазы (рис.6.2). Самая большая сепаратриса соответствует равновесной фазе , она простирается по горизонтали от до и имеет ширину . Самая мала сепаратриса вырождена в точка в центра семейства ( ), она соответствует равновесной фазе . Промежуточные сепаратрисы уменьшают свой размер по мере уменьшения равновесной фазы.

Часто сепаратрису строят в координатах . Такой способ ее представления позволяет оценить энергетический разброс частиц в пучке при захвате в ускорение и в процессе ускорения.

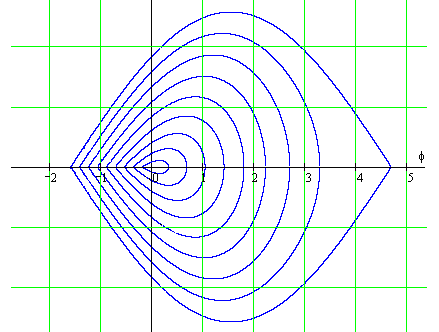
Рис.6.2. Семейство сепаратрис при различных значениях равновесной фазы.

Связь между и определяется выражением (6.15).

При проектировании синхротрона выбор равновесной фазы представляет собой непростую задачу. Так, например, большом значении , близком к , прирост энергии частицы в резонаторе мал (недостаток), размах фазовых колебаний широк, энергетическая неоднородность пучка велика (недостаток). Однако область захвата велика и интенсивность пучка значительна (достоинство). С другой стороны, при малом , близком к нулю, прирост энергии в резонаторе большой (достоинство), размах фазовых колебаний мал и соответственно мала энергетическая неоднородность (достоинство), однако область захвата мала, мала и интенсивность пучка (недостаток).

В пределе обе альтернативные тенденции приводят к неприемлемому результату. Если приять , то разброс энергии будет максимальным, захват будет 100%, но , и пучок ускоряться не будет. Если взять , то темп ускорения будет максимальным, разброс энергий будет отсутствовать, но захват будет равен нулю, а интенсивность пучка (т.е. сам пучок) будет отсутствовать. Поэтому выбор равновесной фазы производится путем компромисса на основе исходных технических требований к ускорителю.

На рисунке 3 приведены два вида потенциальных функций и соответствующие им сепаратрисы. На рисунке 3 (а) фаза синхронной частицы близка к , а на рисунке 3 (б) – к .

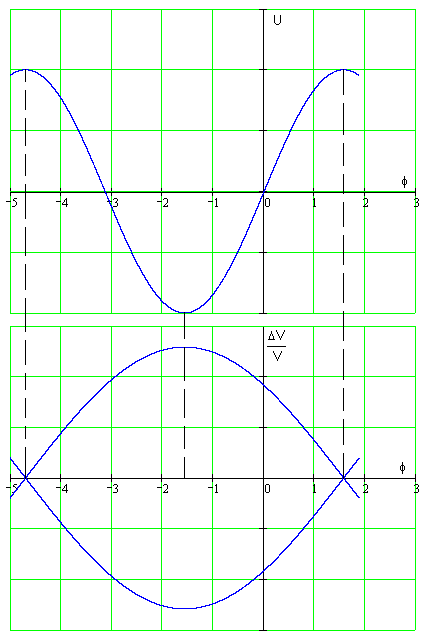
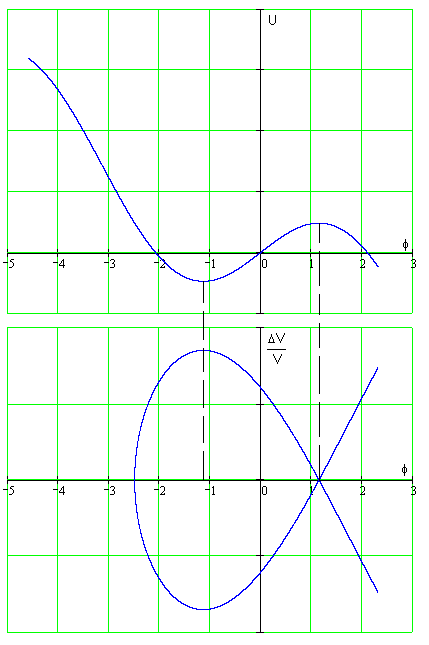а. б.

Рис.6.3. Потенциальные ямы и соответствующие им сепаратрисы.

Рассмотрим характер поведения сепаратрис при переходе энергии частиц через критическую энергию. Для сохранения режима автофазировки величина должна быть больше нуля. Это означает, что при переходе через критическую энергию фаза скачком должна поменять знак. При перемене знака равновесной фазы сепаратриса на фазовой плоскости преобразуется симметрично относительно фазы (рис.6.4).

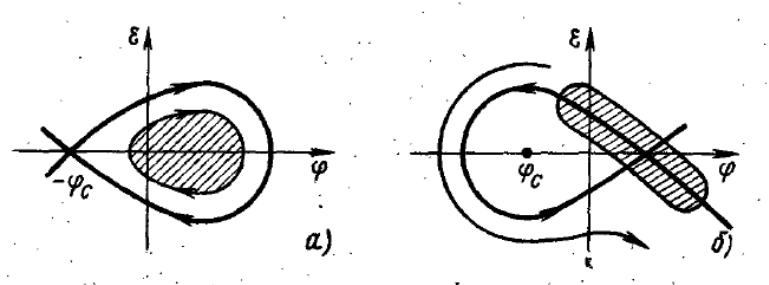
Рис.6.4. Структура фазовой плоскости до а) и после б) перехода через критическую энергию. Заштрихованная область занята частицами.

При переходе через критическую точку и «переворачивание» сепаратрисы частицы на фазовой плоскости оказываются вблизи ее седловой точки и в последующем двигаются по фазовым траекториям, близким к сепаратрисе и лежащим вне и внутри ее. Частицы, оказавшиеся вне области устойчивости будут в дальнейшем потеряны. В очень невыгодном положении оказываются и перезахваченные частицы: т.к. после перехода через критическую точку амплитуда колебаний частиц увеличивается, и они легко выходят из области устойчивости. Таким образом, при переходе через критическую энергию подавляющее большинство частиц должно выпасть из режима ускорения.

Чтобы предотвратить это явление, можно применить следующие методы.

1. Увеличить критическую энергию. Если соответствующим образом исказить магнитную систему, то можно добиться уменьшения коэффициента расширения орбит, а следовательно, увеличения критической энергии. Если критическая энергия больше конечной энергии, то ускоритель всегда работает при энергии ниже критической. Недостаток этого метода – сильное отличие орбиты от круговой, что приводит при той же максимальной магнитной индукции к существенному увеличению среднего радиуса машины.

2. Если в момент перехода энергии через критическое значение резко изменить фазу ускоряющего напряжения на 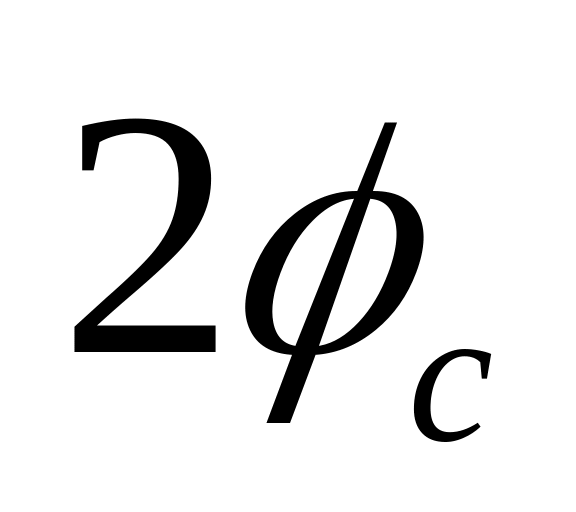, то при этом изображающие точки частиц остаются на месте, а вся картина фазовых траекторий сдвигается так, что они «накрываются» сепаратрисой, соответствующей ускорению при энергии, больше критической (рис.6.5). Для того чтобы осуществить изменение фазы в точно определенный момент, применяют автоматическую систему слежения за пучком. Время, в течении которого изменяется фаза ВЧ-колебаний, необходимо сделать значительно меньше периода синхротронных колебаний.

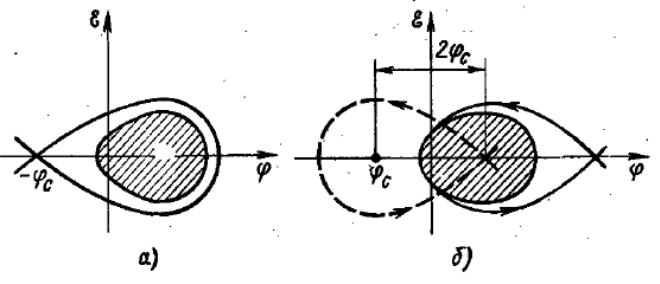
Рис.6.5. Перевод частиц через критическую энергию методом сдвига фазы. Область, занятая частицами, заштрихована; пунктиром показана сепаратриса без сдвига фазы.

В любом случае допуски на параметры ВЧ-системы в районе критической энергии значительно ужесточаются. Поэтому успешное осуществление метода переброса фазы, используемого сейчас повсеместно, в первую очередь зависит от техники автоматического регулирования параметров ускорителя (частоты ускоряющего поля) по данным о движении самого пучка.