
Организация ЭВМ и систем / 351-400
.pdf
Ускорение целочисленного умножения 3 5 1
щей пары разрядов множителя, путем обработки пары 00 как 01, пары 01 как 10, 10 —как 11, а 11 —как 00. В последних двух случаях фиксируется признак коррекции.
Правила обработки пар разрядов множителя с учетом признака коррекции приведены в табл. 7.2. После обработки каждой комбинации содержимое регистра множителя и сумматора частичных произведений сдвигается на 2 разряда вправо. Данный метод умножения требует корректировки результата, если старшая пара разрядов множителя равна 11 или 10 и состояние признака коррекции единичное. В этом случае к полученному произведению должно быть добавлено множимое.
Аппаратные методы ускорения умножения
Традиционный метод умножения за счет сдвигов и сложений, даже при его аппаратной реализации, не позволяет достичь высокой скорости выполнения операции умножения. Связано это, главным образом, с тем, что при добавлении к СЧП очередного частичного произведения перенос должен распространиться от младшего разряда СЧП к старшему. Задержка из-за распространения переноса относительно велика, причем она повторяется при добавлении каждого ЧП.
Один из способов ускорения умножения состоит в изменении системы кодирования сомножителей, за счет чего можно сократить количество суммируемых частичных произведений. Примером такого подхода может служить алгоритм Бута.
Еще один ресурс повышения производительности умножителя — использование более эффективных способов суммирования ЧП, исключающих затраты времени на распространение переносов. Достигается это за счет представления ЧП в избыточной форме, благодаря чему суммирование двух чисел не связано с распространением переноса вдоль всех разрядов числа. Наиболее употребительной формой такого избыточного кодирования является так называемая форма с сохранением переноса. В ней каждый разряд числа представляется двумя битами cs, известными как перенос (с) и сумма (s). При суммировании двух чисел в форме с сохранением переноса перенос распространяется не далее, чем на один разряд.

3 5 2 Глава 7. Операционныеустройства вычислительныхмашин
Это делает процесс суммирования значительно более быстрым, чем в случае сложения с распространением переноса вдоль всех разрядов числа.
Наконец, третья возможность ускорения операции умножения заключается в параллельном вычислении всех частичных произведений. Если рассмотреть общую схему умножения (рис. 7.27), то нетрудно заметить, что отдельные разряды ЧП представляют собой произведения вида aibj, то есть произведение определенного бита множимого на определенный бит множителя. Это позволяет вычислить все биты частичных произведений одновременно, с помощью п2 схем «И». При перемножении чисел в дополнительном коде отдельные разряды ЧП могут иметь вид aibj , aibj или aibj . Тогда элементы "И"заменяются элементами, реализующими соответствующую логическую функцию.
Рис. 7.27. Схема перемножения п-разрядных чисел без знака
Таким образом, аппаратные методы ускорения умножения сводятся:
-к параллельному вычислению частичных произведений;
-к сокращению количества операций сложения;
-к уменьшению времени распространения переносов при суммировании частичных произведений.
Все три подхода в любом их сочетании обычно реализуются с помощью комбинационных устройств.
Параллельное вычисление ЧП имеет место практически во всех рассматриваемых ниже схемах умножения. Различия проявляются в основном в способе суммирования полученных частичных произведений, и с этих позиций используемые схемы умножения можно подразделить на матричные и с древовидной структурой. В обоих вариантах суммирование осуществляется с помощью массива взаимосвязанных одноразрядных сумматоров. В матричных умножителях сумматоры организованы в виде матрицы, а в древовидных они реализуются в виде дерева того или иного типа.
Различия в рамках каждой из этих групп выражаются в количестве используемых сумматоров, их виде и способе распространения переносов, возникающих в процессе суммирования.

Ускорение целочисленного умножения 3 5 3
В матричных умножителях суммирование осуществляется матрицей сумматоров, состоящей из последовательных линеек (строк) одноразрядных сумматоров с сохранением переноса (ССП). По мере движения данных вниз по массиву сумматоров каждая строка ССП добавляет к СЧП очередное частичное произведение. Поскольку промежуточные СЧП представлены в избыточной форме с сохранением переноса, во всех схемах, вплоть до последней строки, где формируется окончательный результат, распространения переноса не происходит. Это означает, что задержка в умножителях отталкивается только от «глубины» массива (числа строк сумматоров) и не зависит от разрядности операндов, если только в последней строке матрицы, где формируется окончательная СЧП, не используется схема с последовательным переносом.
Наряду с высоким быстродействием важным достоинством матричных умножителей является их регулярность, что особенно существенно при реализации таких умножителей в виде интегральной микросхемы. С другой стороны, подобные схемы занимают большую площадь на кристалле микросхемы, причем с увеличением разрядности сомножителей эта площадь увеличивается пропорционально квадрату числа разрядов. Вторая проблема с матричными умножителями — низкий уровень утилизации аппаратуры. По мере движения СЧП вниз каждая строка задействуется лишьоднократно, когдаее пересекает активный фронт вычислений. Это обстоятельство, однако, может быть затребовано для повышения эффективности вычислений путем конвейеризации процесса умножения, при которой по мере освобождения строки сумматоров последняя может быть использована для умножения очередной пары чисел:
Ниже рассматриваются различные алгоритмы умножения и соответствующие им схемы матричных умножителей. Каждый из алгоритмов имеет свои плюсы и минусы, важность которых для пользователя определяет выбор той или иной схемы.
Матричное умножение чисел без знака
Результат Р перемножения двух «-разрядных двоичных целых чисел А и В без знака можно описать выражением
Умножение сводится к параллельному формированию битов из п n-разрядных частичных произведений с последующим их суммированием с помощью матрицы сумматоров, структура которой соответствует приведенной матрице умножения. Схема известна как умножитель Брауна. На рис. 7.28 показан такой умножитель для четырехразрядных двоичных чисел в котором каждому столбцу в матрице умножения соответствует диагональ умножителя. Биты частичных произведений (ЧП) вида aibj формируются с помощью элементов «И». Для суммирования ЧП применяются два вида одноразрядных сумматоров с сохранением переноса: полусумматоры (ПС)1 и полные сумматоры (СМ)2.
1Полусумматором называется одноразрядное суммирующее устройство, имеющее два входа для слагаемых и два выхода — выход бита суммы к выход бита переноса.
2В отличие от полусумматора складывает три числа, то есть имеет три входа для слагаемых и два выхода — выход бита суммы и выход бита переноса.

3 5 4 Глава 7. Операционные устройства вычислительных машин
i
Рис. 7.2а. Матричный умножитель Браунадля четырехразрядныхчисел беззнака
Матричный умножитель n х п содержит п2 схем «И», п ПС и (п2 - 2n) СМ. Если принять, что для реализации полусумматора требуются два логических элемента, а для полного сумматора — пять, то общее количество логических элементов в умножителе составляет пг + 2п + 5(п2 - 2n) - 6пг - 8п.
Быстродействие умножителя определяется наиболее длинным маршрутом распространения сигнала, который в худшем случае (пунктирная линия на рис. 7.28) включает в себя прохождение одной схемы «И», двух ПС и (2n - 4) СМ. Полагая задержки в схеме «И» и полусумматоре равными  , а в полном сумматоре—
, а в полном сумматоре— общую задержку в умножителе можно оценить выражением
общую задержку в умножителе можно оценить выражением  Чтобы сократить ее длительность, n-разрядный сумматор с последовательным переносом в нижней, строке умножителя можно заменить более быстрым вариантом сумматора. Последнее, однако, не всегда желательно, поскольку это увеличивает число используемых в умножителе логических элементов и ухудшает регулярность схемы.
Чтобы сократить ее длительность, n-разрядный сумматор с последовательным переносом в нижней, строке умножителя можно заменить более быстрым вариантом сумматора. Последнее, однако, не всегда желательно, поскольку это увеличивает число используемых в умножителе логических элементов и ухудшает регулярность схемы.
В общем случае задержка в матричных умножителях пропорциональна их разрядности:О(n).
Матричное умножение чисел в дополнительном коде
К сожалению, умножитель Брауна годится только для перемножения чисел без знака. При обработке знаковых чисел отрицательные представляются дополнительным кодом, а матричные умножителя строятся по схемам, отличным от схемы Брауна. Прежде всего, напомним, что запись двоичного числа в дополнительном коде (с дополнением до 2) имеет вид

Ускорение целочисленного умножения 3 5 5
где первый член правого выражения представляет знак числа, а сумма — его модуль.
Исходя из приведенной записи, произведение Р двух «-разрядных двоичных целых чисел А и В дополнительном коде (значение произведения и сомножителей в дополнительном коде обозначим соответственно V(P), V(A) и V(B)) можно описать выражением
Матрица умножения чисел со знаком, представленных в дополнительном коде, похожа на матрицу перемножения чисел без знаков (рис. 7.29). Отличие состоит в том, что (2n - 2) частичных произведений инвертированы, а в столбцы п и (2n - 1) добавлены единицы.
Рис. 7.29. Матрица перемножения п-разрядныхчисел вдополнительном коде
Соответствующая схема матричного умножителя для четырехразрядных чисел показана на рис. 7.30.
Здесь (2n - 2) частичных произведений инвертированы за счет замены элементов «И» на элементы «И-НЕ». Сумматор в младшем разряде нижнего ряда складывает 1 в столбце п с вектором сумм и переносов из предшествующей строки, реализуя при этом следующие выражения:
Инвертор в нижней строке слева обеспечивает добавление единицы в столбец (2n-1).

3 5 6 Глава 7. Операционные устройства вычислительных машин
Рис.7.30. Матричныйумножительдлячетырехразрядныхчиселвдополнительномкоде
Алгоритм Бо-Вули
Несколько иная схема матричного умножителя, также обеспечивающего умножение чисел в дополнительном коде, была предложена Бо и Bули [61]. В алгоритме Бо-Вули произведение чисел в дополнительном коде представляется следующим
Матрица умножения, реализующая алгоритм, приведена на рис. 7.31, а соответствующая ей схема умножителя — на рис. 7.32.
По ходу умножения частичные произведения, имеющие знак «минус», смещаются к последней ступени суммирования. Недостатком схемы можно считать то, что на последних этапах работы требуются дополнительные сумматоры, из-за чего регулярность схемы нарушается.

Ускорение целочисленногоумножения 3 5 7
Рис.7.31.Матриц |
оалгоритмуБо-Вули |
Рис.7.32. Матричный умножительдлячетырехразрядныхчисел вдополнительном коде посхеме Бо-Вули
Алгоритм Пезариса
Еще один алгоритм для вычислений произведения чисел в дополнительном коде был предложен Пезарисом [181].
При представлении числа в дополнительном коде старший разряд числа имеет отрицательный вес. Для учета этого обстоятельства Пезарис выдвигает идею ис- . пользовать в умножителе четыре вида полных сумматоров (рис, 7.33).
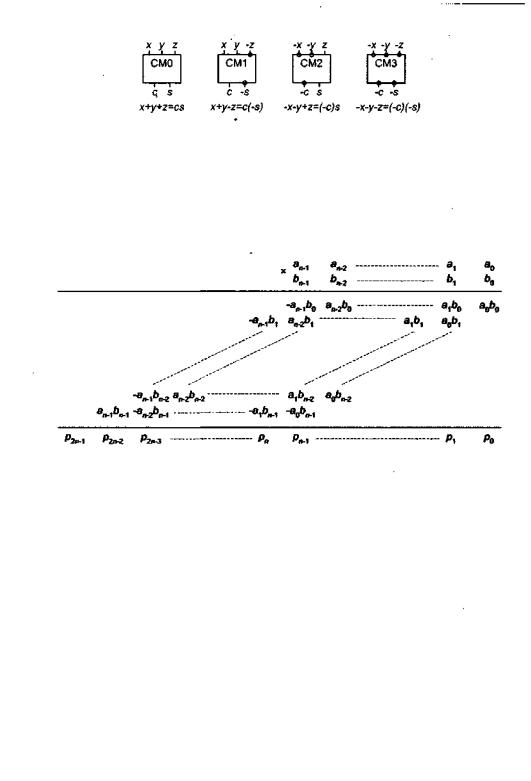
3 5 8 Глава 7. Операционные устройства вычислительных машин
Рис. 7.33. Виды сумматоров, применяемых в матричном умножителе Пезариса
В сумматоре типа СМО, который фактически является обычным полным сумматором, все входные данные (х, у, z) имеют положительный вес, а результат лежит в диапазоне 0-3. Этот результат представлен двухразрядным двоичным числом cs, где с и s также присвоены положительные веса. В остальных трех типах сумматоров некоторые из сигналов имеют отрицательный вес. Схема умножения в рассматриваемом методе показана на рис. 7.34.
Рис. 7.34. Матрица перемножения n-разрядных чисел согласно алгоритму Пеэариса
Здесь знак "минус"- трактуется следующим образом: -1 = -2 * 1 + 1; - 0 = - 2 * *0 + 0. Схемаумножителя, реализующего алгоритм Пезариса, приведена нарис. 7.35, По сравнению с умножителем Бо-Вули, схема Пезариса имеет более регулярный вид, но, с другой стороны, она предполагает присутствие нескольких типов
сумматоров.
Древовидные умножители
Сократить задержку, свойственную матричным умножителям, удается в схемах, построенных по древовидной структуре. Если в матричных умножителях для суммирования п частичных произведений требуется « строк сумматоров, то в древовидных схемах количество ступеней сумматоров пропорционально log2 n(рис. 7.36).
Соответственно числу ступеней суммирования сокращается и время вычисления СЧП. Хотя древовидные схемы быстрее матричных, однако при их реализации требуются дополнительные связи для объединения разрядов, имеющих одинаковый вес, из-за чего площадь, занимаемая схемой на кристалле микросхемы, может оказаться даже больше, чем в случае матричной организации сумматоров. Еще одна проблема связана с тем, что стандартное двоичное дерево не является самой эффективнойдревовидной иерархией,посколькуне позволяетвполноймере

Ускорение целочисленного умножения 3 5 9
Рис. 7.35. Матричныйумножительдля четырехразрядных чисел вдополнительномкодепосхемеПеэариса
Рис.7.36. Суммирование частичныхпроизведений вумножителях: а — о матричной структурой;б—соструктуройдвоичногодерева
воспользоваться возможностями полного сумматора (имеющего не два, а три входа), благодаря чему можно одновременно суммировать сразу три входных бита. По этой причине на практике в умножителях с древовидной структурой применяют иные древовидные схемы. С другой стороны, такие схемы не столь регулярны, как двоичное дерево, а регулярность структуры — одно из основных требований при создании интегральных микросхем.
Древовидные умножители включают в себя три ступени:
-ступень формирования битов частичных произведений, состоящую из n2 элементов «И»;
-ступень сжатия частичных произведений — реализуется в виде дерева параллельных сумматоров (накопителей), служащего для сведения частичных произведений к вектору сумм и вектору переносов. Сжатие реализуется несколь-

3 6 0 Глава7. Операционныеустройства вычислительных машин
кими рядами сумматоров, причем каждый ряд вносит задержку, свойственную одному полному сумматору;
-ступень заключительного суммирования, где осуществляется сложение вектора сумм и вектора переносов с целью получения конечного результата. Обычно здесь применяется быстрый сумматор с временем задержки, пропорциональным O(log2(n)).
Известныедревовидные умножители различаются поспособусокращения чпела ЧП. При использовании в умножителе СМ и ПС их обычно называют счетчиками (3,2) и (2,2) соответственно. Связано это с тем, что код на выходах cs, как и в двоичном счетчике, равен количеству единиц, поданных на входы.
Процесс «компрессии» СЧП завершается формированиемдвух векторов — вектора сумм и вектора переносов, которые для получения окончательного результата обрабатываются многоразрядными сумматорами, то есть различие между древовидными схемами сжатия касается, главным образом, способа формирования упомянутых векторов.
Визвестных на сегодня умножителях наибольшее распространение получили три древовидных схемы суммирования ЧП: дерево Уоллеса, дерево Дадда и перевернутое ступенчатое дерево.
Внаиболее общей формулировке дерево Уоллеса — это оператор с п входами
иlog2n выходами, в котором код на выходе равен числу единиц во входном коде. Вес битов на входе совпадает с весом младшего разряда выходного кода. Простейшим деревом Уоллеса является СМ. Используя такие сумматоры, а также полусумматоры, можно построить дерево Уоллеса для перемножения чисел любой разрядности, при этом количество сумматоров возрастает пропорционально величине log2n. В такой же пропорции растет время выполнения операции умножения.
Согласно алгоритму Уоллеса, строки матрицы частичных произведений группируются по три. Полные сумматоры используются для сжатия столбцов стремя битами, а полусумматоры — столбцов с двумя битами. Строки, не попавшие в набор из трех строк, учитываются в следующем каскаде редукции. Количество строк в матрице (ее высота) на j-й ступени определяется выражениями wо=nиwj + l=2[wj3]+(wjmod3),покаwj>=2
В 32-разрядном умножителе на базе дерева Уоллеса высоты матриц ЧП последовательно уменьшаются в последовательности: 22,15, 10, 7, 5, 4, 3 и 2. Логика построения дерева Уоллеса для суммирования частичных произведений в умно жителе 4x4 показана на рис, 7.37, а. Для пояснения структуры дерева сумматоров часто применяют так называемую точечную диаграмму (рис. 7.37,6). В ней точки обозначают биты частичных произведений, прямыедиагональныелинии представляют выходы полных сумматоров, а перечеркнутые диагонали — выходы полусумматоров. Хотя на рис. 7.37, а в третьем каскаде показаны три строки, фактически после редукции остаются лишь две первых, а третья лишь отражает переносы, которые учитываются при окончательном суммировании. Этим объясняется кажущееся отличие от точечной диаграммы.
