«Изучение вынужденных электрических колебаний» и «исследование затухающих колебаний» Краткая теория

На рис. 1 изображен последовательный колебательный контур, состоящий из конденсатора, соленоида и резистора.

Собственные колебания:

Рассмотрим сначала процессы, происходящие в цепи без активного сопротивления и ЭДС. То есть цепь состоит из конденсатора емкостью С и катушки индуктивностью L. Пусть в начальный момент конденсатор заряжен, и мы замыкаем его на катушку. Конденсатор начинает разряжаться, в цепи появляется возрастающий ток. Следовательно, энергия электрического поля конденсатора будет убывать, а энергия магнитного поля катушки – возрастать. Когда конденсатор полностью разрядится, энергия электрического поля обратится в ноль, а энергия магнитного поля (а следовательно и ток) – достигнет максимального значения. Начиная с этого момента ток будет убывать, а значит, в катушке возникает ток самоиндукции, направленный так, чтобы поддержать уменьшающийся ток разрядки конденсатора. Конденсатор начнет перезаряжаться, в конденсаторе возникнет электрическое поле, стремящееся ослабить ток, и, наконец, мы опять получим заряженный до исходного значения конденсатор в тот момент, когда ток обратится в ноль. Далее эти процессы протекают в обратном направлении.

Запишем второе правило Кирхгофа для нашего контура:

, где - напряжение на конденсаторе, - ЭДС самоиндукции.

Поскольку , а , и учитывая, что , получим:

(1)

Это уравнение гармонических колебаний. Решением его является гармоническая функция

, (2)

где - амплитуда колебаний, - собственная частота колебаний и - начальная фаза. Причем частота определяется только параметрами контура, а амплитуда и фаза находятся из начальных условий. Величина называется периодом колебаний. Из (2) можно получить также и выражения для I(t) и U(t). Поскольку эти колебания не связаны с внешним возбуждением системы, и не зависят от подпитки извне, то они называются свободными или собственными колебаниями системы.

Затухающие колебания:

Добавление в цепь резистора R аналогично включению силы трения в случае механических колебаний. Чтобы учесть это, нам необходимо добавить в (1) падение напряжения на сопротивлении:

(3)

Тогда уравнение (2) перейдет в:

, (4)

где - коэффициент затухания

Решение этого уравнения ищем в виде , тогда после подстановки получим:

Тогда - гармоническая функция, то есть , (но уже с другой частотой , где ) и следовательно

(5)

То есть при условии мы можем описать эту зависимость как гармонические колебания, у которых амплитуда экспоненциально убывает со временем. Такие колебания называются затухающими. Энергия этих колебаний убывает со временем. Зная зависимость заряда на конденсаторе от времени, мы можем написать и зависимость тока на катушке от времени, поскольку . Также можно найти зависимость напряжения на сопротивлении от времени: . Графики всех этих величин выглядят примерно одинаково, отличаясь начальной фазой и амплитудой.

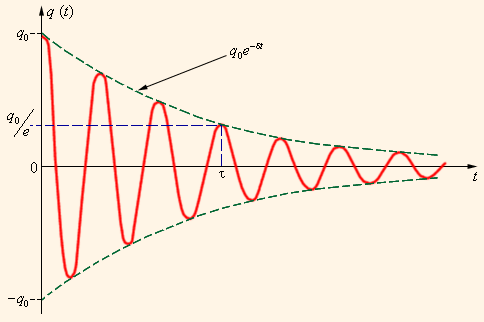
Если же то колебания затухают за время меньше одного периода колебаний. Такое решение называется апериодическим и колебаний в контуре не будет.

Для возникновения колебаний в контуре необходимо, чтобы выполнялось условие . Подставив определения входящих в него величин, мы получим условие

, где (6)

Здесь - критическое сопротивление, при котором колебательный процесс в контуре становится апериодическим.

Затухающие колебания характеризуют коэффициентом затухания , временем релаксации системы (время, за которое амплитуда колебаний уменьшается в e раз), логарифмическим декрементом затухания , показывающим, как изменяется функция за период: , и величиной Q – добротностью контура.

(7)

Чем больше добротность контура, тем меньше затухание в системе.

Вынужденные колебания:

При добавлении в контур переменной ЭДС с амплитудой , то есть , колебания могут перестать затухать, поскольку идет приток энергии из источника, способный компенсировать потери энергии на сопротивлении. Но частота изменения ЭДС в общем случае не совпадает с частотой собственных или затухающих колебаний в контуре. С какой же частотой будут существовать колебания в системе?

По второму закону Кирхгофу для схемы, изображенной на рисунке 1,

или

(8)

Это уравнение аналогично уравнению (4), но с ненулевой правой частью. Нам удобнее будет рассматривать ток, а не заряд. Введем в уравнение коэффициенты затухания и частоту собственных колебаний , получим дифференциальное уравнение вынужденных колебаний

(9)

Из теории линейных дифференциальных уравнений известно, что решением неоднородного дифференциального уравнения является сумма общего решения однородного уравнения (то есть с нулевой правой частью) и любого частного решения неоднородного уравнения. Решение однородного уравнения нам уже известно – мы можем получить его из (5), продифференцировав (5) по времени. Будем тогда искать частное решение в виде: , где

(10)

(11)

Величина называется полным сопротивлением цепи, величина является амплитудой напряжения на кон­денсаторе. Величина называется реактивным емкостным сопротивлением, причём . Величина называется реактивным индуктивным сопротивлением, а амплитуда колебаний напряжения на соленоиде находится как .

Фаза - сдвиг колебаний между колебаниями внешний ЭДС и силой тока в цепи. Ток отстает от напряжения или опережает его в зависимости от соотношения между и .

Таким образом, в системе существуют затухающие колебания с частотой и незатухающие вынужденные колебания с частотой внешней ЭДС . Ясно, что после времени релаксации мы будем наблюдать только вынужденные колебания, так как собственные колебания системы практически исчезнут.

Но если частота изменения ЭДС равна частоте собственных колебаний тока в контуре ( ), то . При этом , то есть изменения тока и ЭДС происходят в фазе. В этом случае полное сопротивление Z становится минимальным и равным R, а амплитуда колебаний силы тока в цепи принимает максимальное значение. Напряжения на конденсаторе и на соленоиде становится одинаковыми по амплитуде и противоположными по фазе ( ). То есть собственные колебания в контуре перестают быть затухающими, поскольку могут забирать энергию из источника (теперь источник и колебания системы согласованы), и складываются с колебаниями от ЭДС. Рассмотренное явление называется резонансом токов. Из (10) следует, что амплитудное значение тока при резонансе . Амплитудное значение напряжения на конденсаторе при резонансе равно

(12)

Здесь добротность контура. Если Q>1, то при резонансе напряжения на соленоиде и на конденсаторе превышают в Q раз ЭДС , приложенную к цепи.

Отметим, что максимум амплитуды колебаний силы тока достигается при частоте , а максимум амплитуды колебаний напряжения на конденсаторе (резонанс напряжений) – при частоте , несколько меньшей . Однако если или

,

то это различие несущественно.