6.5 Сложение случайных процессов

Пусть требуется найти характеристики случайного процесса Z(t), который является суммой случайных процессов X(t) и Y(t), т.е. Z(t)=X(t)+Y(t), если известны их характеристики: .

На основании свойства математического ожидания имеем

, т.е. при сложении случайных процессов их функции математических ожиданий также складываются.

Аналогично при сложении любого числа случайных процессов функция математического ожидания суммы этих процессов будет равна сумме функций математических ожиданий этих случайных процессов, т.е.

.

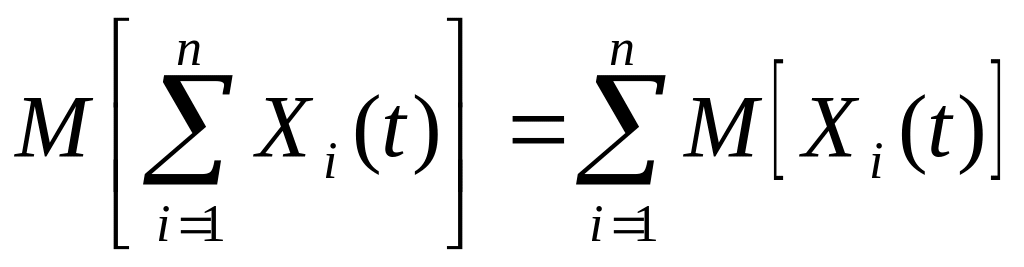Найдем корреляционную функцию , по определению

.

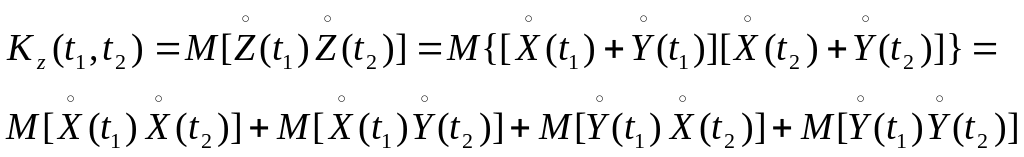Отсюда

,

где - взаимная корреляционная функция случайных процессов X(t) и Y(t);

- взаимная корреляционная функция случайных процессов Y(t) и X(t).

Взаимной корреляционной функцией случайных процессов X(t) и Y(t) называют неслучайную функцию двух аргументов , которая для каждой пары аргументов равна корреляционному моменту между соответствующим сечением случайного процесса X(t) и соответствующим сечением случайного процесса Y(t).

Корреляционную функцию часто называют автокорреляционной функцией.

При сложении произвольного числа случайных процессов корреляционная функция суммы случайных процессов будет равна сумме автокорреляционных функций плюс сумма взаимных корреляционных функций, т.е.

.

Если случайные процессы не коррелированны, то . Тогда

.

Сложение случайного процесса со случайной величиной. Пусть требуется найти характеристики случайного процесса Z(t), который является суммой случайного процесса X(t) и случайной величины Y, т.е. Z(t)=X(t)+Y, если известны их характеристики: .

В случае независимости случайного процесса X(t) и случайной величины Y функцию математического ожидания суммы можно определить по формуле .

6.6 Произведение случайной и неслучайной функций

Пусть требуется найти характеристики случайного процесса Z(t), который является произведением случайной функции X(t) и неслучайной функции Q(t), т.е. Z(t)=Q(t)*X(t), если известны их характеристики: .

Используя свойство функции математического ожидания, можно записать, что функция математического ожидания произведения случайной функции X(t) и неслучайной функции Q(t) будет равна произведению неслучайной функции Q(t) на функцию математического ожидания случайной функции X(t), т.е.

.

На основе определения корреляционной функции случайного процесса можно записать, что

.

Откуда корреляционная функция произведения случайной и неслучайной функций будет равна произведению неслучайной функции Q(t) в сечениях на корреляционную функцию случайной функции X(t), т.е.

.

6.7 Стационарные случайные процессы

На практике встречаются процессы, которые имеют вид непрерывных случайных колебаний относительно некоторого среднего значения. При этом средняя амплитуда и характер этих колебаний с течением времени существенно не изменяется; их реализации имеют примерно одинаковый характер. Такие процессы относят к стационарным случайным процессам.

Случайный процесс называют стационарным, если n-мерная плотность вероятности не меняется при любом сдвиге всей группы точек вдоль оси времени, т.е.

. (6.10)

Примерами таких процессов являются: шумы в приемнике после его включения; шумы ламп, полупроводниковых приборов, резисторов, колебания самолета на установившемся режиме полета, случайные ошибки автоматических систем относятся к стационарным случайным процессам (рис. 6.7).

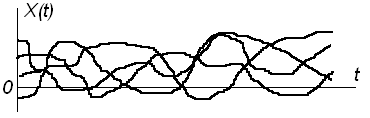
Рисунок 6.7 – Реализации стационарного случайного процесса

К нестационарным случайным процессам обычно относят, например, шумы приемника при его включении, модулированные по амплитуде и частоте шумовые колебания, потребление электроэнергии в городе в течение суток и другие не установившиеся случайные процессы (рис. 6.8).

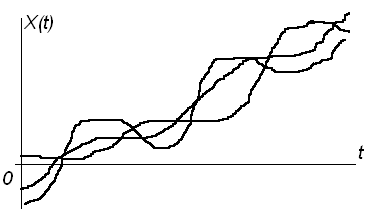
Рисунок 6.8 – Нестационарные случайные процессы

Случайный процесс X(t), у которого вероятностные характеристики при любом совпадают с соответствующими характеристиками случайного процесса , называют стационарным в узком (строгом) смысле.

Случайный процесс X(t) называют стационарным, если математическое ожидание является постоянным, а корреляционная функция зависит только от разности аргументов, т.е. , а . Такой случайный процесс является стационарным в широком смысле.

Из определения стационарности процесса вытекает, что среднее значение во всех сечениях процесса остается постоянным и не зависит от времени. Это значит, что оно является характеристикой не отдельных сечений, а процесса в целом. При этом математическое ожидание характеризует положение реализаций относительно оси абсцисс. Если оно равно нулю, то это означает, что отклонения в положительную и в отрицательную сторону в среднем одинаковы.

Корреляционная функция стационарного случайного процесса характеризуется следующими основными свойствами.

1 Дисперсия стационарного случайного процесса постоянна и равна значению корреляционной функции в начале координат, т.е.

.

2 Корреляционная функция стационарного случайного процесса является четной, т.е.

.

График корреляционной функции геометрически представляет собой симметричную относительно оси ординат кривую. Часто в различных приложениях встречается показательная корреляционная функция (рис. 6.9).

.

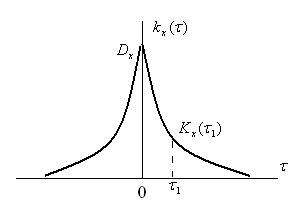
Рисунок 6.9 – График показательной корреляционной функции

Нормированная корреляционная функция стационарного случайного процесса , представляет собой коэффициент корреляции, зависящий только от величины .

Эргодическое свойство стационарного случайного процесса. Для отыскания характеристик стационарного случайного процесса необходимо знать одномерную и двумерную плотности распределения этого процесса, или располагать достаточно большим числом реализаций процесса, чтобы с незначительной погрешностью определить значения характеристик.

Однако на практике, с одной стороны возникают существенные трудности в получении аналитических выражений одномерной и двумерной плотностей распределения стационарного случайного процесса, а с другой стороны исследователь, как правило, ограничен небольшим числом реализаций стационарного случайного процесса, в отдельных же случаях он не может получить более одной реализации процесса.

Возможность определения вероятностных характеристик по одной реализации стационарного случайного процесса достаточно большой продолжительности установил русский математик А. Я. Хинчин.

Случайный процесс называется эргодическим, если любая ее реализация несет в себе всю информацию о случайном процессе.

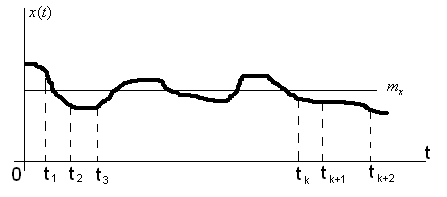
Рисунок 6.10 – Реализация стационарного случайного процесса

Эргодическое свойство имеют те стационарные случайные функции, которые не содержат в своем составе обыкновенную случайную величину.

Если стационарная случайная функция X(t) обладает эргодическим свойством, то:

а) ее математическое ожидание приближенно равно средней по времени ординате одной произвольно взятой реализации достаточно большой продолжительности (рис. 6.10):

; (6.11)

б) значение корреляционной функции при любом значении приближенно равно произведению отклонения одной реализации в точках, отстоящих друг от друга на величину , от математического ожидания стационарной случайной функции

. (6.12)

Если , то и

. (6.13)

На практике формулами (6.11), (6.12) и (6.13) для определения приближенных характеристик не пользуются, так как аналитический вид реализации , как правило, неизвестен.

Поэтому интегралы (6.11), (6.12) и (6.13) заменяют конечными суммами, для чего реализацию на промежутке делят на n равных частей, длина каждого из которых равна . Тогда математическое ожидание, дисперсия и корреляционная функция будут определяться соответственно следующими выражениями:

, (6.14)

, (6.15)

. (6.16)

Если выполняется равенство , то стационарная случайная функция называется эргодической по отношению к математическому ожиданию; если же справедливо равенство , то – эргодической по отношению к корреляционной функции.

Во многих случаях удобно пользоваться достаточным условием эргодичности случайной функции

.

Расчет корреляционной функции существенно облегчается, если применяется аппарат гармонического анализа, операции которого выполняются без затруднений, благодаря наличию подробных таблиц.