Композиция двух нормально распределенных случайных векторов

Пусть имеется один случайный вектор с параметрами и второй вектор с параметрами . При этом оба вектора подчиняются нормальному закону и являются независимыми между собой. Требуется определить закон распределения суммы этих векторов.

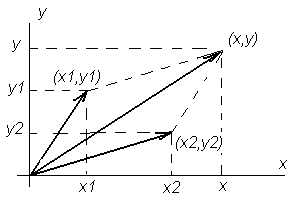
Рисунок 4.3 – Композиция случайных векторов

Из построений на рис. 4.3 следует, что случайные координаты суммарного вектора можно определить как суммы координат случайных векторов и , т. е.

.

Поскольку плотности распределения и являются нормальными, то и плотность распределения также будет подчиняться нормальному закону с параметрами: . Аналогично и для координаты Y: .

Так как координаты X и Y по условию задачи зависимы между собой, то необходимо найти их корреляционный момент, который в этом случае будет равен

.

При композиции двух нормально распределенных случайных векторов суммарный вектор также подчиняется нормальному закону распределения с параметрами: .

Вопросы для повторения

1 Как определяется математическое ожидание суммы нескольких случайных величин (зависимых и независимых)?

2 Как рассчитать дисперсию суммы нескольких случайных величин (зависимых и независимых)?

3 Числовые характеристики линейной функции случайных аргументов.

4 Докажите теорему произведения нескольких независимых случайных величин.

5 По выражению какой числовой характеристики можно определить математическое ожидание произведения двух зависимых случайных величин?

6 Как определить дисперсию произведения двух зависимых случайных величин?

7 Математическое ожидание и дисперсия нелинейной функции случайных аргументов.

8 Запишите выражения для функции распределения и плотности вероятности суммы двух случайных величин.

9 Что называется композицией законов распределения?

10 Почему центральная предельная теорема Ляпунова имеет широкое применение на практике?

Упражнения

4.1 Случайная величина Y связана линейно со случайной величиной X по закону Y=2X+1. Случайная величина X имеет равновероятное распределение в интервале (3;7). Найдите математическое ожидание случайной величины Y.

4.2 Случайная величина Y связана со случайной величиной X зависимостью . Случайная величина X имеет экспоненциальное распределение с интенсивностью . Найдите математическое ожидание случайной величины Y.

4.3 Найдите математическое ожидание случайной величины Z=X*Y, если случайные величины X и Y не зависимы и распределены по равновероятному закону в интервале (1;5) и (7;11) соответственно.

4.4 Найдите математическое ожидание случайной величины Z=X*Y, если случайные величины X и Y имеют M(X)=2, M(Y)=2.5 и корреляционный момент, равный 2.5.

4.5 Вычислите дисперсию комплексной случайной величины , если известны среднеквадратичные отклонения случайных величин X и Y, равные .

4.6 Определите математическое ожидание комплексной случайной величины , если случайные величины X и Y не зависимы и распределены по равновероятному закону в интервале (4;10) и (2;6) соответственно.

4.7 Случайные величины X и Y распределены по нормальному закону с параметрами: . Определите параметры закона распределения случайной величины Z=X+Y.

4.7 Определите параметры закона распределения случайной величины , если случайные величины независимы и распределены равновероятно с одинаковыми математическими ожиданиями и дисперсиями, равными .

4.8 Определите параметры закона распределения случайной величины , если случайные величины независимы и распределены экспоненциально с одинаковыми параметрами, равными .

4.9 Определите математическое ожидание случайной величины , если случайные аргументы распределены равновероятно в интервалах (0;5), (5;7), (2;6) соответственно.

4.10 Определите дисперсию случайной величины Y линейно связанной со случайной величиной X выражением , если эти случайные величины независимы и дисперсия случайной величины X равна D(X)=0.7.