§ 3. Эвристические методы снижения размерности

Описанные выше методы сокращения размерности факторного пространства (метод главных компонент и модели факторного анализа) допускали интерпретацию в терминах той или иной строгой вероятностной модели и, следовательно, подразумевали возможность исследования свойств рассматриваемых процедур в рамках теории математической статистики (см, п. 3., §1,2 настоящей главы). В данном параграфе речь пойдет о методах, подчиненных некоторым частным целевым установкам (наименьшее искажение геометрической структуры исходных «выборочных точек», наименьшее искажение их эталонного разбиения на классы и т. д.), но не формулируемых в терминах вероятностно-статистической теории³. Процедура выбора той или иной целевой установки, подходящей именно для данной конкретной задачи, практически не формализована, носит эвристический характер, т. е.. как правило, обусловливается лишь опытом и интуицией исследователя. Поэтому мы и будем называть такие методы эвристическими.

Надо признаться, что при отсутствии априорной или выборочной предварительной информации о природе исследуемого вектора наблюдений и о генеральных совокупностях, из которых эти наблюдения извлекаются, точно в таком же невыгодном положении находятся методы, факторного анализа и главных компонент. Однако для них все-таки существует принципиальная возможность теоретического обоснования (при наличии соответствующей дополнительной информации), в то время как эвристические методы не претендуют и на это.

Хочется подчеркнуть, что факт описания здесь методов снижения размерности, не использующих предварительной информации, например, обучающих или квазиобучающих выборок, следует расценивать лишь как следствие признания неизбежности ситуаций, в которых мы такой информации не имеем, но не как стремление рекламировать эти методы в качестве наиболее эффективных. В действительности же обоснованное и эффективное решение задач снижения размерности без слепой надежды на удачу, можно, по нашему мнению, получить лишь на пути глубокого профессионального анализа, дополненного статистическими методами, использующими предварительную выборочную (обучающую) информацию.

1. Методы, не использующие обучающих выборок

а) Нелинейное отображение выборочных точек в пространство меньшей размерности, наименее искажающее их геометрическую конфигурацию. Пусть, как обычно, X₁, Х₂, ..., Хn—результаты p-мерных наблюдений, «снятые» на n исследуемых объектах. И пусть d*_ij = _E(Хi,Xj) =- евклидово расстояние между точками Xi и Xj в исходном p-мерном пространстве.

Метод, предложенный в работе [31], состоит в нелинейном однозначном отображении п данных точек (векторов) из p-мерного исходного факторного пространства R^p в пространство меньшей размерности. Особенно важны отображения в двух- или трехмерное пространство (р'=2,3), так как полученная там конфигурация из п точек поддается непосредственному графическому изображению. Ставится цель минимально (в некотором смысле) исказить исходную конфигурацию из n точек. Опишем этот метод и укажем некоторые возможности его модификации.

Пусть в результате некоторого однозначного отображения (проекции) П имеющиеся у нас исходные многомерные наблюдения

Xi = , (i=1,2, ..n)

преобразованы (спроектированы) в соответствующие n наблюдений

Yi= (i=1,2, ..n)

расположенные в пространстве r^p'меньшей размерности, т. е. Yi = П (Xi).

При переходе от конфигурации Х₁, Х₂, .... Х_n к конфигурации Y₁,Y₂, ...,Yn, попарные расстояния d*_ij между исходными точками Xi и Xj преобразуются в расстояния d_ij= _E (Yi, Yj). В качестве меры искажения конфигурации исходных точек введем величину , которую естественно рассматривать как функцию от переменных (v= 1,2, ...,p', i= 1,2, ,.., п):

(,, …,)=

Предлагается следующая эвристическая итерационная процедура подбора переменных с целью минимизации функции

(,, …,,..,). Пусть _m =,

ошибка отображения после m-й итерации, где с= и d*_ij(m)=. Следующая (m+1)-я итерация задается:

=-_iv(m), где

_iv(m)=

а  определено эмпирически (автор [31] использовал   0,3 или 0,4). На первом шаге итерационной процедуры набор Y₁, Y₂,.., Yп фиксируется случайным образом или находится с помощью метода главных компонент (см. § 1 настоящей главы).

На ряде примеров удалось показать, что данная процедура приводит к отображению П, которое достаточно хорошо сохраняет некоторые геометрические свойства исходной конфигурации точек.

Так, в качестве исходных данных брались 9 точек, расположенных на прямой в R⁹ на равных расстояниях друг от друга; после применения к ним описанной выше процедуры, задающей преобразование П, па плоскости были получены точки, лежащие на одной прямой.

При отображении конфигурации из 8 точек, лежащих на окружности в R⁹ на равных расстояниях друг от друга, и центра этого круга, на плоскости R² были получены точки, лежащие практически на окружности, и центр круга. В обоих случаях начальное приближение на плоскости выбиралось случайно, а  = 10^-16; исходные данные одномерны в 1-м и двумерны во 2-м случае, поэтому отображение на плоскость можно провести с нулевой ошибкой.

При отображении набора из 30 точек, равномерно распределенных на 3-мерной спирали, была получена конфигурация из точек на синусоидальной криво и примерно равноотстоящих друг от друга.

Следующий пример показывает, что метод нелинейных отображений может давать лучшие результаты, чем метод главных компонент [30].

Даны 5 сферических 4-мерных гауссовских распределений специального вида, из каждого делается выборка по 15 точек. Оказалось, что при нелинейном отображении исходной конфигурации в R² на плоскости можно выделить 5 групп точек, причем эти группы соответствуют исходным группам.

При отображении методом главных компонент удается выделить только 4 группы точек. Две исходные группы точек после проектирования на плоскость оказались полностью «перекрытыми».

Во всех рассмотренных примерах сходимость алгоритма была получена за 20 и менее шагов.

Возможности применения данного метода ограничены, с одной стороны, видом или сложностью распределений, из которых были сделаны выборки, и, с другой стороны, общим количеством точек. При попытке применить алгоритм для анализа выборок из очень сложных распределений высокой размерности оказалось, что ошибка отображения слишком велика ( >>0,1), и двумерная конфигурация резко искажает исходную. В то же время есть основания предполагать, что описанный метод может быть успешно использован для анализа таких данных, которые содержат выборки из гиперсферических и гиперэллиптических распределений.

Отметим, что данный метод требует большого объема оперативной памяти машины, поэтому общее числа точек ограничено (у автора [31] максимальное значение п = 250), При п > 250 целесообразно объединять наблюдения в группы и заменять группу некоторым ее представителем (например, центром группы), сокращая таким образом число векторов («Замечание о методах предварительной обработки классифицируемых наблюдений» см. в конце главы [1]). Данная процедура сравнительно проста, она не зависит от вида распределений элементов выборки, не требуется никакой априорной информации об этих распределениях. Можно предложить следующие два видоизменения данного алгоритма. Во-первых, рассмотрим

()=

При растяжении каждого вектора Yi в  раз (=Yi) расстояние между преобразованными точками так же, как легко видеть, растянется в  раз, т.е. =_E (,)= d_ij, так что

()=-+=

=1-2+ (4.33)

Из (4.33) следует, что min достигается при

= (4.34)

В то же время, очевидно, что наилучшее в смысле минимума функции ошибки  значение  равно 1 (иначе конфигурацию можно «растянуть», уменьшив значение ), следовательно.

(4.35)

Представляется целесообразным на каждом шаге итерационной процедуры «растягивать» все векторы в  раз по формуле (4.34), уменьшая тем самым значения функции ошибки. Из сказанного следует, что условие (4.35) является необходимым условием минимума функции ошибки в смысле преобразования «растяжения» всех векторов конфигурации.

Во-вторых, оставаясь в рамках тех же качественных критериев близости конфигурации исходной и преобразованной совокупностей точек, можно предложить использовать вместо функции ошибки  более гладкую (бесконечно дифференцируемую) функцию новых координат, например:

=(,, …,,..,)=

=

Рассмотрим подробнее случай р'= 2. Обозначим

Z=(z⁽¹⁾_, z⁽²⁾,…, z^(2n-1), z⁽²ⁿ⁾)= (,, …,,)

вектор в 2 n-мерном пространстве;

- норма вектора Z,

(Z₁ , Z₂ )= - скалярное произведение векторов Z₁ и Z₂

^~(Z)= ^~( z⁽¹⁾_, z⁽²⁾,…, z^(2n-1), z⁽²ⁿ⁾)=

= =

=.

Выпишем в явном виде первые производные функции ^~:

= 

= 

где с=

Пусть z⁽¹⁾= z⁽²⁾.= z⁽³⁾ =0, z⁽⁴⁾ >0

Тогда легко показать, что выполняются следующие условия:(Z) О,

Q = {Z :  (Z) с} - ограниченное множество, где с -произвольная константа,

-градиент функции (Z) удовлетворяет условию Липшица на множестве Q, так как ’(Z) - непрерывно дифференцируемая вектор-функция.

Следовательно, для нахождения минимума функции (Z) применим метод сопряженных градиентов [11], а именно, следующую итерационную процедуру

Z(m+1)=Z(m)-_mU(m)

U(m)= - ’[Z(m)]+_m U(m-1), m=0,1…

где Z(m) и U(m) — векторы, полученные на m-м шаге, а коэффициенты _m и _m находятся из условий:

_m : [ Z(m)-_mU(m)]=[ Z(m)-_mU(m)]

_m=

Можно доказать, что для любого начального приближения такой алгоритм сходится в смысле

=0

где под (m) понимается так называемый нижний предел функции (m), т. е. (n). Заметим, что экспериментальные исследования метода сопряженных градиентов показывают, что на практике наблюдается не только сходимость на подпоследовательностях (т. е. по нижнему пределу), но и обычная сходимость, т. е= 0.

б) Метод экстремальной группировки признаков. При изучении сложных объектов, заданных многими параметрами, возникает задача разбиения параметров на группы, каждая из которых характеризует объект с какой-либо одной стороны. Но получение легко интерпретируемых результатов осложняется тем, что во многих приложениях измеряемые параметры (признаки) лишь косвенно отражают существенные свойства, которыми характеризуется данный объект.

Так, в психологии измеряемые параметры — это реакции людей на различные тесты а выражением существенных свойств, общими факторами, являются такие характеристики, как тип нервной системы, работоспособность и т. д.

Оказывается, что во многих случаях изменение какого-либо общего фактора сказывается неодинаково на измеряемых признаках, в частности, исходная совокупность из р признаков обнаруживает такое естественное «расщепление» на сравнительно (с р) небольшое количество групп, при котором изменение признаков, относящихся к какой-либо иной группе, обусловливается в основном каким-то одним общим фактором, своим для каждой такой группы. После принятия этой гипотезы разбиение на группы естественно строить так, чтобы параметры, принадлежащие к одной группе, были коррелированы сравнительно сильно, а параметры, принадлежащие к разным группам - слабо. После такого разбиения для каждой группы признаков строится случайная величина, которая в некотором смысле наиболее сильно коррелирована с параметрами данной группы; эта случайная величина интерпретируется как искомый фактор, от которого существенно зависят все параметры данной группы.

Очевидно, подобная схема является одним из частных случаев общей логической схемы факторного анализа, В отличие от ранее описанных классических моделей факторного анализа при так называемом экстремальном подходе [5], группировка признаков и выделение общих факторов делаются на основе экстремизации некоторых эвристически введенных функционалов. Разбиение, оптимизирующее данный функционал, называется экстремальной группировкой параметров. Таким образом, под задачей экстремальной группировки набора случайных величин x⁽¹⁾, х⁽²⁾..., х^(p), а заранее заданное число классов р' понимают отыскание такого набора подмножеств S₁, S₂, ..,S_p' натурального ряда чисел 1, 2,..., р, что ={1, 2, ..., р),a S_l= при lq, и таких р' нормированных (т. е. с единичной дисперсией Df⁽ⁱ⁾= 1) факторов f⁽¹⁾, f⁽²⁾.... f^(p'), которые максимизируют какой-либо критерий оптимальности.

Следуя [5], остановимся здесь на алгоритмах для двух различных критериев оптимальности.

Первый алгоритм экстремальной группировки признаков в качестве критерия оптимальности использует функционал

J₁ =+

в котором под соr (х, f) понимается обычный парный коэффициент корреляции между признаком х и фактором f[1]. Обозначим A_l ={x⁽ⁱ⁾, i  S_l}, l =1, 2, ..., р'. Максимизация функционала J₁, (как по разбиению признаков на группы A₁,., А_р', так и по выбору факторов f⁽¹⁾, f⁽²⁾..., f^(p') )отвечает требованию такого разбиения параметров, когда в одной группе оказываются наиболее «близкие» между собой, в смысле степени коррелированности, признаки: в самом деле, при максимизации функционала J₁ для каждого фиксированного набора случайных величин f⁽¹⁾, f⁽²⁾..., f^(p') в одну l-ю группу будут попадать такие признаки, которые наиболее сильно коррелированы с величиной f^(l) ; в то же время среди всех возможных наборов случайных величин f⁽¹⁾, f⁽²⁾..., f^(p') будет выбираться такой набор, что каждая из величин f^(l) в среднем наиболее «близка» ко всем признакам своей группы.

Очевидно, что при заданных классах S₁, S₂, ..., S_p' оптимальный набор факторов f⁽¹⁾, f⁽²⁾..., f^(p') получается в результате независимой максимизации каждого слагаемого

(l=1,2,...,р'),

откуда

где _l — максимальное собственное значение матрицы _l, составленной из коэффициентов корреляции переменных, входящих в A_l. При этом отимальный набор факторов f^(l) l=1,2, .... р' задастся формулами

f^(l) =, l=1,2,…p’ (4.36)

где

r_ij=cor(x⁽ⁱ⁾,x^(j)), а ^(l)=(₁^(l), …,_ml^{( l)})

—собственный вектор матрицы _l, отвечающий максимальному собственному значению _l, т. е.

_l ^(l) = _l ^(l)

С другой стороны, считая известными факторы f⁽¹⁾, f⁽²⁾..., f^(p'), нетрудно построить разбиение S₁, S₂ .... S_р', максимизирующее J₁при фиксированных f⁽¹⁾, f⁽²⁾..., f^(p'), а именно:

S_l={i:cor²(x⁽ⁱ⁾,f^(l))cor²(x⁽ⁱ⁾,f^(q)) для всех q= 1, 2, ..., р'. (4.37)

Заметим, что соотношения (4,36) и (4.37) являются необходимыми условиями максимума J₁.

Для одновременного нахождения оптимального разбиения S₁, S₂ .... S_р' и оптимального набора факторов f⁽¹⁾, f⁽²⁾..., f^(p') предлагается итерационный алгоритм, чередующий выбор оптимальных (по отношению к разбиению, полученному на предыдущем шаге) факторов и выбор разбиения оптимального к факторам, полученным на предыдущем шаге.

Пусть на v-м шаге итерации построено разбиение параметров на группы A₁ ..., Ар'. Для каждой такой группы параметров строят факторы f⁽¹⁾_v по формуле (4.36) и новое (v + 1) разбиение параметров A₁^(v+1) ..., А_р'^(v+1) в соответствии с правилом: параметр x⁽ⁱ⁾ относится к группе A_l^(v+1), если

cor²(x⁽ⁱ⁾,f_v^(l))cor²(x^(q),f_v^(q)) для всех l= 1, 2, ..., р'. (4.38)

Если для некоторого параметра x⁽ⁱ⁾ найдутся два или более факторов таких, что для x⁽ⁱ⁾ и этих факторов в (4.38) имеет место равенство, то параметр x⁽ⁱ⁾ относится к одной из соответствующих групп произвольно.

Очевидно, что на каждом шаге итераций функционал J₁ не убывает, поэтому данный алгоритм будет сходиться к максимуму. Максимум может быть локальным.

Для описания второго алгоритма экстремальной группировки признаков введем функционал

J₂=++…+

В содержательном смысле функционал J₂ похож на функционал J₁, и его максимизация также соответствует основному требованию к характеру разбиения признаков на группы. В [5] показано, что имеет место следующее утверждение. Необходимыми и достаточными условиями максимума функционала J₂ являются:

—разбиение параметров на группы A₁ ..., Ар'. таково, что функционал

J₂ =

(где gi —некоторые числовые коэффициенты, равные либо +1 либо —1) достигает максимума как по разбиению на группы, так и по значениям коэффициентов gi. Здесь под Dz понимается, как обычно, дисперсия случайной величины z;

—факторы f^(l) определяются соотношениями

f^(l) = (4.39)

Логическая схема доказательства этого факта следующая. Сначала, варьируя функционал J₂ и используя метод множителей Лагранжа для учета условия D f^(l)= 1, показывают что в точке максимума функционала J2 фактор f^(l) имеет вид (4,39). Затем доказывается, что если f^(l) имеет вид (4.39), то при любом наборе коэффициентов gi = ±1 и любом разбиении параметров на группы имеет место соотношение J₂>= J₃, а если же J₃ достигает максимума, то J₂ = J₃. Из этого утверждения следует, в частности, что для нахождения групп S_l и факторов f^(l) достаточно максимизировать функционал J₃. При фиксированном разбиении на группы функционал J₃ достигает максимума тогда, когда для каждого l соответствующие коэффициенты gi максимизируют величину:

(4.40)

Поэтому естественно воспользоваться рекуррентной процедурой максимизации J₃. В процедуре циклически перебираются переменные х⁽¹⁾, х⁽²⁾,.., x^(p') и на каждом шаге принимается решение об отнесении очередного параметра х^(j) к одной из групп A₁, ..., А_p' и определяется знак g_i.

Пусть к v-му шагу алгоритма построены разбиения параметров на группы A₁^(v), ..., А_p ^(v)_' вычислены коэффициенты g₁^(v),..., g₁^(v) равные плюс или минус единице, и пусть на этом шаге рассматривается признак x⁽ⁱ⁾ A₁^(v). Тогда строятся р' вспомогательных коэффициентов g_i,l^(v+1) (I = 1,...p')по формуле

g_i,l^(v+1) =sign ji⁴

и для всех l=1,2, ..., р' вычисляются разности

_l^(v+1) =

Затем выбирается такой номер l = l*, что

_l^(v+1) =

и признак x⁽ⁱ⁾ исключается из группы A_i и присоединяется к группе a_i*; остальные группы признаков на этом шаге не меняются. В результате получаем новое разбиение признаков —

A₁^(v+1), ..., А_p ^(v+1)_'

Новые значения коэффициентов g_i.l* ^(v+1)определяются по формулам:

g_j ^(v+1) = g_j ^(v) для ji, g_i ^(v+1) = g_j,l* ^(v)

На следующем (v + 1)-м шаге алгоритма рассматривается параметр x⁽ⁱ⁺¹⁾ если i р, и x⁽¹⁾, если i = р.

Процедура заканчивается, если при рассмотрении всех признаков очередного цикла сохранились как разбиения признаков на группы, так и значения всех коэффициентов; полученное разбиение и значения коэффициентов рассматриваются как оптимальные.

Для демонстрации сходимости метода к локальному максимуму в [5] доказывается, что на каждом шаге алгоритма значение Jз не убывает.

Нетрудно проследить идейную близость метода экстремальной группировки признаков с методами, опирающимися на логическую схему факторного анализа. Так, например, отправляясь от общей модели вида

x⁽ⁱ⁾ =

(см. (4,9) и (4-20)), первую компоненту f⁽¹⁾ и «нагрузки» l_1i в методе главных компонент можно определять, как мы видели (см. п. 2 § 1 глава IV) из условия минимума выражения

при нормирующем ограничении

Df⁽¹⁾=1

Решение этой условно-экстремальной задачи очевидным образом сводится к нахождению максимума выражения

при условии Df⁽¹⁾=1

Для построения следующего фактора f⁽²⁾ (второй главной компоненты) рассматриваются случайные величины

x⁽ⁱ²⁾ =x⁽ⁱ⁾-cor(x⁽ⁱ⁾ ,f⁽¹⁾) f⁽¹⁾

Для этих случайных величин аналогичным образом находится следующий фактор f⁽²⁾ и так далее.

Очевидно, что при реализации первого алгоритма метода экстремальной группировки признаков для каждой группы признаков A_l строится фактор, имеющий смысл 1-й главной компоненты для этой группы в смысле метода главных компонент.

В центроидном методе (см. § 2 глава IV) общий фактор ищется в виде

f⁽¹⁾= (4.41)

где gi =1 и gi выбирается так, чтобы максимизировать величину

Df⁽¹⁾=D() (4..42)

Сравнение выражений (4.41) и (4.42) с выражениями (4.39) и (4.40) показывает, что максимизация функционала J₂ приводит к построению для каждой группы признаков фактора, отличающегося на некоторый множитель от первого общего фактора, который был бы построен для, этой группы центроидным методом.

в) Метод корреляционных плеяд. Задача разбиения признаков на группы часто имеет и самостоятельное значение. Например, в ботанике для систематизации вновь открытых растений делают разбиения набора признаков на группы, так, чтобы 1-я группа характеризовала бы форму листа, 2-я группа — форму плода и т. д. В связи с этим и возник эвристический метод корреляционных плеяд [7], [12], [13].

Метод корреляционных плеяд так же, как и метод экстремальной группировки, предназначен для нахождения таких групп признаков-«плеяд», что корреляционная связь, т. е. сумма модулей коэффициентов корреляции, между параметрами одной группы (внутриплеядная связь) достаточно велика, а связь между параметрами из разных групп (межплеядная) — мала.

А именно, по определенному правилу, но корреляционной матрице признаков образуется чертеж-граф, который затем с помощью различных приемов разбивают на подграфы. Элементы, соответствующие каждому из подграфов, и образуют плеяду.

Рассмотрим корреляционную матрицу R = (r_ij), i, j = 1, 2, ..., р исходных признаков. Нарисуем р кружков; внутри каждого кружка напишем номер одного из признаков. Каждый кружок соединяется линиями со всеми остальными кружками; над линией, соединяющей i-й и j-й элементы (ребром графа), ставится значение модуля коэффициента корреляции rij. Полученный таким образом чертеж рассматриваем как исходный граф.

Задавшись (произвольным образом или на основании предварительного изучения корреляционной матрицы) некоторым пороговым значением коэффициента корреляции r0, исключаем из графа все ребра, которые соответствуют коэффициентам корреляции, по модулю меньшим r0. Затем задаем некоторое r1 > r0 и повторяем описанную процедуру. При некотором достаточно большом r граф распадется на несколько подграфов, т. е. таких групп кружков, что связи (ребра графа) между кружками различных групп отсутствуют. Очевидно, что для полученных таким образом плеяд внутриплеядные коэффициенты корреляции будут больше r, а межплеядные — меньше r.

В другом варианте корреляционных плеяд [7] предлагается упорядочивать признаки и рассматривать только те коэффициенты корреляции, которые соответствуют связям между элементами в упорядоченной системе.

Упорядочивание производится на основании принципа максимального корреляционного пути, а именно: все р признаков связываются при помощи (p-1) линий (ребер) так, чтобы сумма модулей коэффициентов корреляции была максимальной. Это достигается следующим образом: в корреляционной матрице находится наибольший по абсолютной величине коэффициент корреляции, например r_l,m = r(1) (коэффициенты на главной диагонали матрицы, равные единице, не рассматриваются).

Рисуем кружки, соответствующие параметрам x^(l) и х^(m), и над «связью» между ними пишем значение r(1). Затем, исключив r(1), находим наибольший коэффициент в m-м столбце матрицы),о соответствует нахождению признака, который наиболее сильно после х^(l) «связан» с x^(m)) и наибольший коэффициент в 1-и строке матрицы (это соответствует нахождению признака, наиболее сильно после х^(m) «связанного» с х^(l). Из найденных таким образом двух коэффициентов корреляции выбирается наибольший — пусть это будет rlj= r(2). Рисуем кружок х^(j), соединяем его с кружком х^(l) и проставляем значение r(2). Затем находим признаки, наиболее сильно связанные с х^(l), х^(m) и х^(j)), и выбираем из найденных коэффициентов корреляции наибольший. Пусть это будет r_jq = r(3). Требуем, чтобы на каждом шаге мы получили новый признак, поэтому признаки, уже изображенные на чертеже, исключаются, следовательно, ql, qm, qj. Рисуем кружок, соответствующий x^(q), соединяем его с х^(j) и т. д. На каждом шаге находятся параметры, наиболее сильно связанные с двумя последними рассмотренными параметрами, а затем выбирается один из них, соответствующий большему коэффициенту корреляции. Процедура заканчивается после (р -1)-го шага; граф оказывается состоящим из р кружков, соединенных (p-1) линией. Затем задается пороговое значение r, а все линии, соответствующие меньшим, чем r коэффициентам корреляции, исключаются из графа.

Назовем незамкнутым графом такой граф, для которого для любых двух кружков существует единственная траектория, составленная из линий связи, соединяющая эти два кружка. Очевидно, что во втором варианте метода корреляционных плеяд допускается построение только незамкнутых графов, а в первом варианте такое ограничение отсутствует.

Поэтому разбиения на плеяды, полученные разными способами, могут не совпадать.

В работе [10] приводятся результаты экспериментальной проверки алгоритмов экстремальной группировки параметров, а также сравнение полученных результатов с результатами, даваемыми методом корреляционных плеяд.

Эксперимент проводился на физиологическом материале: исследовались влияния шумов и вибрации на работоспособность и самочувствие. Снимались 33 признака (р = 33), из них 7 параметров, характеризующих температуру тела; 4—кровяное давление; 14— аудиометрию (т. е. порог слышимости на заданной частоте); 2 — дыхание; 4 — силу и выносливость рук и 2 (обособленных параметра) — пульс и скорость реакции.

С точки зрения физиолога «идеальным» было бы разбиение, при котором все характеристики температур образовали бы отдельную группу; параметры, характеризующие давление — свою отдельную группу и т. д., обособленные параметры образовали бы группы, состоящие из одного элемента. Наиболее близким к «идеальному» оказалось разбиение, полученное вторым алгоритмом экстремальной группировки, хотя алгоритм и присоединяет обособленные параметры к другим группам. Наименее точные (среди трех сравниваемых алгоритмов) результаты дал метод корреляционных плеяд.

г) Снижение размерности с помощью кластер-процедур. В ряде ситуаций удобно рассматривать признаки x⁽ⁱ⁾(i = 1, 2, ..., р), как одномерные наблюдения и использовать многократное повторение этих наблюдений (на n исследуемых объектах) для введения и вычисления таких естественных мер близости между объектами (признаками) x⁽ⁱ⁾ и х^(j)какими являются в данном случае абсолютная величина коэффициента корреляции r_ij или корреляционное отношение _ij (по поводу вычисления r_ijи _ij, и их свойств см., например, [1])⁵.

Следуя идее обобщенного (степенного) среднего (см. § 1 главы [1]), введем в качестве меры близости групп признаков A_l и A_q величину

(4.43)

где  — некоторый числовой параметр, выбор конкретного значения которого находится в нашем распоряжении, а т_v—число признаков, составляющих группу A_v. Аналогично вводится средняя мера близости R(A_l) признаков, входящих в одну группу

R(A_l) =R_l,l^() = (4.44)

Если желаемая размерность р' (р' < р) задана заранее, то исходные р признаков х⁽¹⁾, х⁽²⁾, ..., x^(p) разбивают на р' однородных групп одним из двух способов: либо последовательно объединяя в одну группу два наиболее близких, в смысле r_ij или R_l,q^() признака (или признак и группу, или две группы) до тех пор, пока не останется ровно р' групп (иерархическая кластер-процедура), либо находя такое разбиение исходных признаков на р' групп, при котором усредненная мера внутригрупповой близости признаков

была бы максимальной. Последнего обычно удается добиться с помощью простого перебора вариантов, так как общее число признаков р, как правило, не превосходит несколько десятков, a p' — несколько единиц. После этого от каждой группы следует отобрать по одному представителю, используя для этого технику метода главных компонент или факторного анализа (отдельно внутри каждой группы).

Если же желаемая размерность р' заранее не определена, то разбиение исходных признаков на группы, а следовательно, и выбор неизвестного р', можно подчинить задаче максимизации функционала типа

+Z_

где Z_,—введенная в предыдущей главе мера концентрации разбиения, т. е.

Z_ =

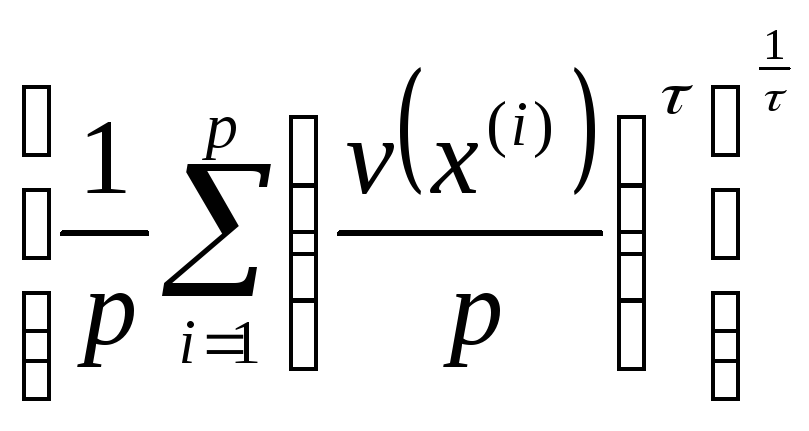
Здесь v(x⁽ⁱ⁾) — число признаков в группе, содержащей признак х⁽ⁱ⁾. Можно воспользоваться также и двойственной формулировкой экстремальной задачи разбиения объектов (признаков) на неизвестное число групп (см. § I, глава III).

2. Выявление наиболее информативных признаков при наличии обучения

Исследователь находится в несравненно более выгодных условиях, если он располагает так называемыми обучающими выборками, т. е. порциями (пусть небольшими) наблюдений

X_1i,X_2i, ...X_mi,i (i=l, 2, ..., k, т=т₁+т₂+...+т_k) (4.45)

о каждой из которых известно, что она извлечена из какого-то одного класса (представляет один из исследуемых «образов»), причем эти порции представляют все k исследуемых классов (образов).

При наличии обучающих выборок (4.45) и при заданном алгоритме классификации  задачу выявления наиболее информативных признаков можно сформулировать следующим образом: для любого наперед заданного р' <р указать такой набор признаков

= (х^(q1), х^(q2), .... х^(qp')), (4.46)

отобранных из числа исходных р признаков x⁽¹⁾, x⁽²⁾, …, x^(p), классификация по которому (т. е. при игнорировании всех остальных р — р' признаков) с помощью заданного алгоритма  т элементов обучающей выборки приводила бы к наименьшей средней доле ошибочно расклассифицированных наблюдений (4.45).

То есть подвектор вектора Х должен обладать тем свойством. что

(4.47)

Здесь - число неправильно расклассифицированных (с помощью алгоритма ) наблюдений i-й обучающей выборки (при классификации по набору признаков Х^(p') размерности р').

Если известны априорные вероятности _i (i=l, 2, ..., k) появления наблюдения i-го класса (т. е. _i —это удельный вес наблюдений i-го класса в совокупности всех мыслимых наблюдений), то набор Х^(p')() определяют из условия минимизации взвешенной средней доли ошибочно расклассифицированных наблюдений обучающие выборок, т. е.

(4.48)

а) Методы перебора вариантов. Будем называть пространство размерности р'<p наиболее информативным (относительно заданного алгоритма классификации ), если его координаты обладают свойством (4.47) (или свойством (4.48) в байесовской постановке, т. е. при наличии априорных вероятностей _i). Очевидно, наиболее информативное подпространство может быть определено с помощью метода полного перебора вариантов, при котором для каждого из C_p^p’ вариантов наборов из р' признаков подсчитывается средняя доля q ошибочно расклассифицированных наблюдений обучающих выборок и выбирается тот набор, при котором q = = min. Однако такой метод требует огромного объема вычислений. Объем вычислений можно сократить, использовав метод Монте-Карло или метод случайного поиска. Метод Монте-Карло отличается от полного перебора тем, что значения q находятся не для всех подпространств размерности р', а только для некоторых. Эти подпространства выбираются случайным образом из множества всех подпространств в предположении, что все подпространства равновероятны.

Назовем эффективным подпространством признаков такие подпространства Х_эф^(p’) на которых значения q отличаются от минимального значения на некоторую достаточную малую величину  (, задается заранее). Случайный поиск ведется до нахождения любого Х_эф^(p’)

Поясним на примере, насколько метод Монте-Карло может уменьшить число «перебираемых» подпространств по сравнению с методом полного перебора.

П р и м е р. Пусть k=3, p=17, признаки распределены нормально с одной и той же ковариационной матрицей во всех трех классах, причем корреляция для различных пар признаков колеблется от 0,01 до 0,9; т = 250 (m₁ = 84, m₂ = 92, т₃ = 74). Алгоритм классификации  задается соответствующим образом построенной (см. главу I) линейной дискриминантной функцией.

Для нахождения и _эф для р' = 3 проводился полный перебор подпространств (С₁₇₀³ = 680), и для каждого подпространства находилось значение v = v₁ + v₂ +v₃, чего, как легко видеть, достаточно для оценки q в случае

₁ =₂ =…=_k = и m₁  m₂  … m_k

Был построен график дискретной функции N(v), показывающий, сколько подпространств соответствует различным значениям v.

Оказалось, что v_min = 88,и нашлось только одно подпространство для которого v = 88.

Пусть Х_эф⁽³⁾ - любое подпространство, для которого v <=95. Из графика N(v) было определено, что таких подпространств всего 16. Следовательно, при независимой выборке подпространств

P{ v <=95}=

Можно показать, что с вероятностью 0,95 хотя бы одно из 126 случайно выбранных подпространств окажется _эф. Таким образом, метод Монте-Карло с высокой степенью вероятности (в среднем в 95 случаях из ста) даст значительный выигрыш в вычислениях: 126 подпространств вместо 680.

Метод, названный случайным поиском с адаптацией (СПА), [8], является улучшением метода Монте-Карло. В отличие от чистого метода Монте-Карло этот метод состоит в случайном поиске подпространства Х_эф^(p’) с «поощрением» и «наказанием» отдельных признаков, x⁽¹⁾, x⁽²⁾, ..., x^(p). Для этого в начале поиска задаются вероятности выбора каждого из признаков x⁽¹⁾, x⁽²⁾, ..., x^(p); если перед началом поиска нет информации о предпочтительности выбора какого-либо признака, то полагаем =.

«Поощрение» и «наказание» признаков x⁽¹⁾, x⁽²⁾, ..., x^(p) сводится к изменению вероятностей выбора признаков на следующих этапах поиска в зависимости от результатов предыдущих этапов. Предполагаем, что ₁ =₂ =…=_k и m₁  m₂  … m_k и в качестве оценки информативности подпространства рассмотрим v =-общее число неправильно расклассифицированных наблюдений обучающих выборок. После анализа некоторого числа r случайно выбранных подпространств X₁^(p’), X₂^(p’), ..., X_r^(p’) находим подпространства Х_1.min и X_1.max, дающие минимальное v_min, и максимальное v_max значения из всех r подсчитанных значений v. Далее, увеличиваем вероятность выбора каждого из признаков, составивших Х ^(p’)_1.min на некоторую добавочную вероятность h. После такого поощрения проводим наказание признаков, на которых построено Х ^(p’)_max уменьшая вероятности выбора на величину h. Значения v_1.min и v_1.max посылаем в рабочие ячейки ₁ и ₂

При измененных вероятностях выбора каждого из признаков x⁽¹⁾, x⁽²⁾, ..., x^(p) с помощью соответствующим образом построенного случайного эксперимента получаем новую группу подпространств и находим Х^(p’)_2.min и X^(p’)_2.max, соответствующие v_2.min и v_2.max. Новое поощрение и пересылку v_2.min в ячейку ₁делаем только тогда, если v_2.min < v_1.min а наказание и пересылку v_2.max. в ячейку ₂ , если v_2.max > v_1.max.

Далее поступаем аналогично. В результате такого поиска получаем в ячейке ₁ некоторое v_min = min { v_i.min }⁶.

Поиск прекращается, если содержимое ячейки ₁ сохраняется на протяжении некоторого числа групп. За подпространство Х_эф^(p’) принимается подпространство, соответствующее v_min

Метод СПА был использован для нахождения Х_эф^(p’) уже рассмотренном примере, т. е.: р = 17; р' = 3; k == 3; т₁ = 84; т₂ = 92;m₃ = 74.

Поиск ₁ проводился без поощрения и наказания, поиск ₂ -с поощрением и наказанием (h = 0,013). При поиске ₃ первоначальные вероятности выбора признаков () устанавливались различными в соответствии со значениями средней доли ошибочно расклассифицируемых наблюдений обучающих выборок (q), полученными отдельно для каждого из признаков, т. е. при р'= 1.

Число r подпространств, анализируемых на каждом этане алгоритма, равно 10. На рис. 4.8 изображена сходимость величины v_i.min к v_min при различных видах поиска. На оси абсцисс откладывается суммарное число подпространств R, которые были рассмотрены к данному моменту поиска. Из рис. видно, что при поиске ₃ понадобилось всего 4 группы (40 подпространств) для получения v_min = 88 (а при методе ₂ -120).

Этот эксперимент показывает целесообразность применения данного метода для определения наиболее информативной системы признаков

В общем виде вопрос о выборе r и h не решен. Вероятно, что чем больше r и меньше h, тем больше вероятность получения Х^(p’) и тем больше потребуется машинного времени. Предполагается также, что с увеличением числа сочетаний выигрыш в количестве вычислений, который дает данный метод по сравнению с методом полного перебора, увеличивается.

б

Рис. 4.8. Сравнение различных алгоритмов поиска наилучшей комбинации признаков

) Последовательное рассмотрение отдельных признаков (метод Кендалла). В работе [25] предлагается метод построения наиболее информативного набора признаков, не зависящий от типа распределения. Рассматривается задача распознавания двух образов, т. е. решается вопрос, как зная 2 обучающие выборки из двух многомерных генеральных совокупностей, определить, к которой из этих совокупностей относится некоторый элемент. Метод, которым решается задача, состоит в том, что признаки сначала упорядочиваются «по старшинству», в порядке убывании их информативности, а затем строится решающее правило, по которому по значению старшего признака некоторого элемента либо можно отнести этот элемент к одной из генеральных совокупностей, либо перейти к следующему по старшинству признаку. В случае, если после перехода к самому младшему признаку по его значению нельзя распознать данный элемент, задача остается нерешенной.

Рассмотрим пример: генеральные совокупности - это 2 сорта ириса: «Разноцветный» и «Вирджиния».

Берется по 50 цветков каждого сорта и делается 4 линейных измерения специального вида (ширины лепестков и т. д.). Следуя [25], обозначим эти четыре признака через PL, PW, SL, SW.

Данные измерений двух сортов ириса по 4 переменным приводятся в табл. 4.4.

Таблица 4.4

Сорт "Paзноцветный"				Сорт "Вирджиния"
SI.	SW	PL	PW	SL	SW	PL	PW
7,0	3,2	4,7	1,4	6,3	3,3	6,0	2,5
6,4	3,2	4,5	1,5	5,8	2,7	5,1	1.9

Примечание. В каждом столбце по 50 значений, измерения производили с точностью до 0,1

Используя табл. 4.4, составляем таблицу частостей по каждому из признаков. Так, в табл. 4.5 приведены частости для признака PL двух сортов ириса. Этот признак, как выяснится позже, является старшим в данной задаче.

Таблица 4.5

Значения переменных	Сорт "Разноцветный"	Сорт "Вирджиния»	Значения переменных	Сорт "Разноцветный»	Сорт "Вирджиния"
4,3	25	-	5,2	-	2
4,4	4	-	5,3	-	2
4,5	7	1	5,4	-	2
4,6	3	-	5,5	-	3
4,7	5	-	5,6	-	6
4,8	2	2	5,7	-	-
4,9	1	3	5,8	-	3
5,0	1	3	5,9	-	13
5,1	1	7

Примечания, В правой части таблицы приводится количество цветков, для которых измерение по PL равно данному значению.

Из таблицы видно, что по переменной PL множества измерений цветков обоих сортов пересекаются на отрезке (4.5; 5,1); т. е. левее отрезка попадают только измерения «Разноцветного», правее только «Вирджиния», а внутри отрезка содержатся измерения обоих сортов. Обозначим этот отрезок через R_PL., а через N_PL — число цветков обоих сортов, измерения которых по PL попадают вне отрезка R_PL. Аналогично введем n_sl, N_PW, Nsw. По табл. 4.5 подсчитаем N_PL, N_PW, n_sl и Nsw. Оказалось, что N_PL = 63; N_PW = 62, a n_sl <. N_PW, Nsw <N_PW.

Следовательно, по переменной PL можно распознать максимальное число элементов (цветков), поэтому считаем PL — старшим признаком, PW — следующим по старшинству, так как Nsw и n_sl < N_PW и строим следующее решающее правило:

PL < 4,4 относим цветок к сорту «Разноцветный»

PL > 5,2 относим цветок к сорту «Вирджиния»

4,5<PL<5,1 переходим к следующему по старшинству признаку.

Всего элементов, которые нельзя распознать по PL, т. е. тех. для которых значения PL попадают в R_PL , - 37 (37 = 50 + 50—63). Выбираем эти элементы из табл. 4.4 и составляем для них по PW таблицу, аналогичную таблице 4.5, отражающую распределение частостей для 37 элементов, не распознанных по PL. Затем находится Rpw, строится решающее правило по PW анлогично (*), определяется старшийиз оставшихся признаков.

После построения решающего правила для «самого младшего» признака процедура распознавания заканчивается. Элементы, которые нельзя распознать с помощью такой процедуры, считаются неопределенными, Этот метод очень прост; никаких вычислений, кроме подсчета случаев, в нем не содержится. Процедура распознавания не зависит от вида распределений совокупностей; не требуется никакой априорной информации об этих распределениях. При применении процедуры выясняется, какой из признаков более информативный в том смысле, но какому из них можно определить большее число случаев. Если с помощью такой процедуры удается распознать очень мало случаев, рекомендуется перейти к новым координатам. Попробуем наглядно пояснить смысл этой рекомендации.

Из рис. 4.9 видно, что R_x(1) и R_x(2) велики, и по признакам x⁽¹⁾ и x⁽²⁾ не удается распознать ни одного элемента. После поворота осей (переход к координатам y⁽¹⁾ и y⁽²⁾) получаем области A, В, С, D, в которых можно распознать элементы, и область Е — «область неопределенности» .

В общем случае предлагается переходить к координатам, совпадающим с главными компонентами одной из выборок. Но вопрос о том, действительно ли при этом уменьшится число неопределенных элементов, не исследован. Естественным критерием качества такой процедуры можно считать долю «неопределенных» точек по аналогии с долей ошибочно распознанных точек.

Рис. 4,9. Переход к новым координатам в методе Кендалла

1 В некоторых случаях к этому условию добавляется требование специального вида матрицы остаточных дисперсий, а именно V == ²I

2Аналогичную задачу классификации ткачих при исследовании их производительности труда см. в п.4 предыдущего параграфа.

3Отсутствие строгой вероятностно-статистической модели, лежащей в основе тех или иных методов, не исключает возможности использования отдельных вероятностно-статистических понятий и соответствующей терминологии, как это имеет место, например, в методе экстремальной группировки факторов, в методе корреляционных плеяд и некоторых других

4 1 при x>0,

sign x= 0 при х=0,

-1 при x<0.

5Если для описания меры близости между x⁽ⁱ⁾ и x^(j) используется корреляционное отношение, то предварительно целесообразно произвести симметризацию этой меры, рассматривая в качестве симметричной характеристики степени близости этих признаков величину , где _ij обычное корреляционное отношение переменной х⁽ⁱ⁾ по переменной x^(j)[1, с. 108].

6 Заметим, что при неограниченном поощрении и наказании признаков не исключена ситуация, в которой вероятность выбора некоторого признака НИ окажется или отрицательной, или большей единицы.

Конечно, вероятность такого события очень мала (вследствие малости h и большого числа признаков), и, кроме того, в рассмотренных в работе [8] примерах показано, что на практике алгоритм сходится значительно раньше, чем вероятность выбора какого-либо из признаков окажется близкой к 0 или 1. Тем не менее целесообразно ввести следующее ограничение: пусть 0 < M₁ < М₂ < 1, где M₁ и M₂ — некоторые заранее выбранные числа.

В случае, если на l-м шаге окажется, что — h < М₁ или + h > М₃, где х⁽ⁱ⁾- некоторый признак, попавший в подпространство, дающее соответственно v_l.min или v_l.max, то положим на (l + 1)-м шаге: =М₁ или = M₂. При этом наказание или поощрение остальных признаков нужно провести таким образом, чтобы .