анализа вида (4.20). Другими словами, сущность задачи минимизации (по В_m и У (m)) величины (4.24) состоит в следующем. Первый из т общих факторов y⁽¹⁾(т) находится из условия, чтобы попарные корреляции между исходными признаками были как можно меньше, если влия­ние на них этого фактора y⁽¹⁾(m) учтено. Следующий общий фактор y⁽²⁾(m) находится из условия максимального ослабления попарных корреляционных связей между исходными признаками, оставшихся вне учета влияния первого общего фактора y⁽¹⁾(m) и т. д. Из сказанного, в частности, следует, что методы главных компоненты факторного анализа должны давать близкие результаты в тех случаях, когда главные компоненты строятся по корреляционным матрицам исходных признаков, а остаточные дисперсии _ii сравнительно невелики.

3 а м е ч а н и е. Вопрос о существовании модели факторного анализа. По-видимому, не всякая ковариационная матрица  допускает представление вида (4.21), а следовательно, не всякий вектор наблю­дений Х допускает интерпретацию в рамках модели факторного анализа типа (4.20). Очевидно, условия представимости вектора наблюдений Х в рамках модели факторного анализа должны формулироваться в терминаx свойств ковариационной матрицы , а также в виде некоторых соотношении между размерностью исходного пространства р и числом общих факторов р'. Одним из наиболее общих (но малоконструктивных) результатов такого рода является, например, следующее утверждение:

для того чтобы вектор Х допускал представление вида (4.20), необходимо и достаточно, чтобы существовала диагональная матрица V с неотрицательными элементами такая, что матрица  — V была бы неотрицательно-определенной и имела бы ранг р'. Более детальное и конст­руктивное исследование условий существования модели факторного анализа читатель сможет найти, например, в [16]. Заметим лишь, что изучение проблемы существования (разрешимости уравнений (4.20)) модели факторного анализа даст основу для построения различных статистических критериев адекватности модели по отношению к исследуемым наблюдениям Х₁, Х₂, ..., Х_n

2. Вопросы идентификации модели факторного анализа

Будем в дальнейшем предполагать, что имеется по меньшей мере одно решение (Q, V) уравнений (4.21). При исследовании вопроса единственности решения системы (4.21) относительно (Q, V) (при заданных _ij.) следует различать два аспекта проблемы. Во-первых, надо понять, при каких дополнительных условиях па искомую мат­рицу нагрузок Q и на соотношение между р и р' не может существовать двух различных решений Q⁽¹⁾ и Q⁽²⁾ таких, чтобы одно из них нельзя было бы получить из другого с помощью соответствующим образом подобранного ортогонального преобразования С (единственность с точностью до ортогонального преобразования, или с точностью до вращения факторов). Оказывается [16], достаточным условием единственности такого рода является требование к матрице Q, чтобы при вычеркивании из нее любой строки оставшуюся матрицу можно было бы разделить на две подматрицы ранга р', откуда автоматически следует требование

(4.25)

Можно показать, что для р' = 1 и р' = 2 это условие является одно временно и необходимым, откуда, в частности, следует, что случаи (р = 2, р' = 1) и (р = 4, р' = 2) по допускают идентификации мо дели факторного анализа в указанном выше смысле (более подробное исследование идентификации этого типа можно найти в [16]).

Будем предполагать далее, что имеется по меньшей мере одно решение (Q, V) системы (4.21) и что оно единственно с точностью до ортогонального преобразования.

Вставляя в уравнения (4.21) вместо найденного решения (Q, V) другую пару матриц (QC, V), где С — матрица (размера р'р') любого ортогонального преобразования, легко убедиться, что и она (эта пара матриц) удовлетворяет данной системе уравнений. Следовательно, возвращаясь к модели (4.20), получаем, что наряду с общими факторами Y ⁼ (y⁽¹⁾,..., y^(p'))' можно рассмотреть (при тех же нагрузках q_ij) общие факторы Z = СУ. Поскольку, как известно, ортогональное преобразование координат У геометрически означает вращение осей y⁽¹⁾,..., y^(p') около начала координат на некоторый угол, то получается, что при отсутствии дополнительных условий на природу искомой матрицы нагрузок Q общие факторы y⁽¹⁾,..., y^(p') могут быть определены лишь с точностью до вращения системы координат в соответствующем p'-мерном пространстве. Существует несколько вариантов дополнительных условий на класс матриц Q, в котором следует искать решение системы (4,21), обеспечивающих уже окончательную однозначность решения (Q, V). От конкретного содержания этих условий зависит и способ численного выявления структуры искомой модели и соответственно способ статистического оценивания неизвестных пара метров q_i,j, v_ij и факторов y⁽¹⁾. Поэтому мы остановимся на них параллельно с описанием методов статистического исследования модели факторного анализа.

3. Определение структуры и статистическое исследование модели факторного анализа

Итак, в распоряжении исследователя — последовательность многомерных наблюдений Х₁, Х₂, ..., Х_n, и он хочет с помощью модели (4.20) перейти от исходных коррелированных признаков х⁽¹⁾,..., ..., х^(p), являющихся компонентами каждого из наблюдений, к меньшему числу некоррелированных вспомогательных признаков (общих факторов) y⁽¹⁾,..., y^(p'). Для этого надо суметь определить оценки неизвестных нагрузок остаточных дисперсий v^{^}_ii и, наконец, самих общих факторов у⁽ⁱ⁾.

Как упоминалось, в основной модели (4.20) при р' > 1 оказывается слишком много неизвестных параметров для их однозначного определения. Поэтому вначале исследователь должен выбрать какую-то систему дополнительных априорных соотношений, связывающих неизвестные параметры модели, которые делают решение задачи однозначным и позволяют получить относительно простое частное решение системы (4,21). Затем он может отказаться от этих дополнительных соотношений, подбирая с помощью подходящего ортогонального преобразования (вращения осей) тот вариант оценок нагрузок q^_ij и остаточных дисперсий v_ij, который ему кажется предпочтительнее в основном с точки зрения возможности содержательной интерпретации получаемых при этом общих факторов и их нагрузок,

а) Различные варианты дополнительных априорных соотношений между qij и vij, постулируемых исследователем с целью однозначной идентификации анализируемой модели:

1) решение (Q, V) системы (4.21) ищется лишь в классе таких матриц Q и V, для которых матрица

Q'VQ

имеет диагональный вид, причем диагональные элементы этой матрицы различны и упорядочены в порядке убывания¹;

2) из всех решений системы (4.21) выбирается лишь то, для которого

матрица

Q'Q

диагональна, причем все диагональные элементы различны и упорядочены (в порядке убывания);

3) решение системы (4.21) ищется лишь среди таких матриц Q, которые для заранее заданной матрицы (размера р  р') В = (b_ij), i = 1, ..., р, j = 1, ..., р' ранга р' удовлетворяют требованию

B'Q=D=

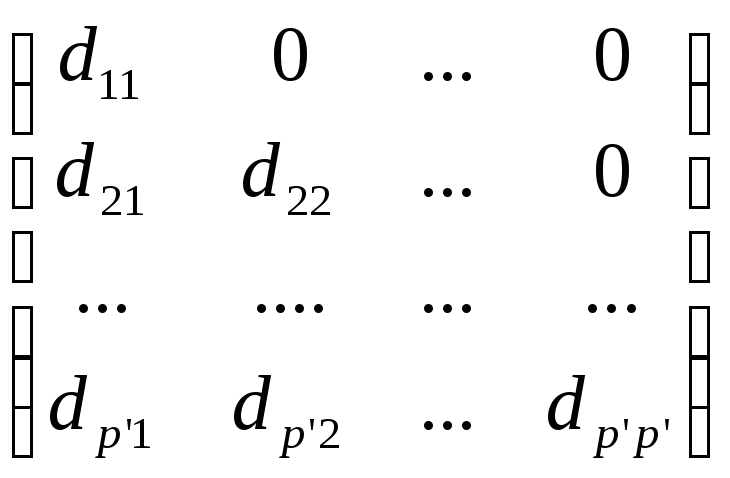
В частности, выбор

B'=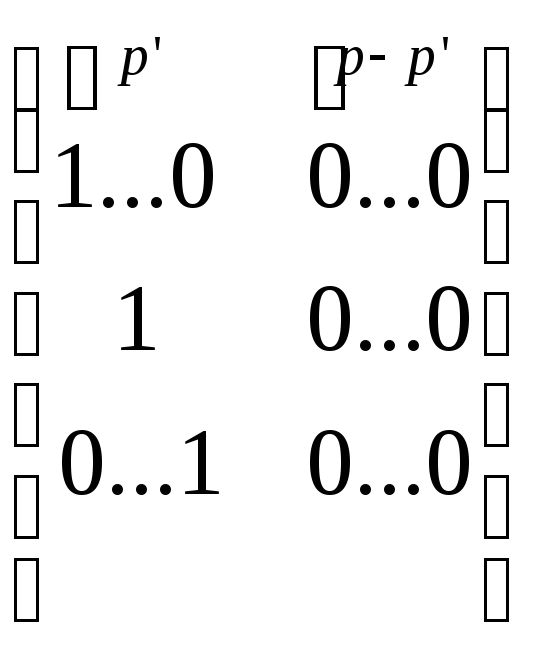

приводит к ограничению на Q типа

Q =

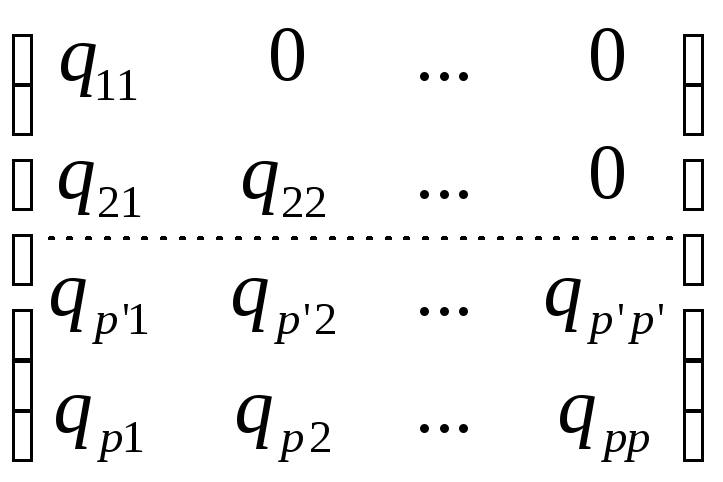
что означает: первый исходный признак x⁽¹⁾ должен выражаться только через один первый общий фактор y⁽¹⁾, второй признак y⁽²⁾ — через два общих фактора y⁽¹⁾ и y⁽²⁾ и т. д.

Можно, кстати, показать, что при соответствующем выборе вспомогательной матрицы B определение искомых, параметров модели приводит к решению ранее сформулированной экстремальной задачи (4.24).

Содержательную интерпретацию условий 3) следует искать в ситуациях, когда исследователь располагает некоторой априорной информацией, из которой можно, во-первых, извлечь реальный гипотетический смысл общих факторов и, во-вторых, постулировать наличие определенного числа нулевых элементов в матрице нагрузок Q (с более или менее точным указанием их «адреса»), что означает априорное отрицание факторов y^(j)(j=1,2...p') исходных признаков x⁽¹⁾ от некоторых из общих факторов y^(j)(j=1,2...p'). Эта же идея реализуется и в других, менее формализованных вариантах дополнительных условий («простые структуры», «нулевые элементы в специфических позициях» [16]), на которых мы здесь не будем останавливаться.

б) Описание общего итерационного подхода к. выявлению структуры модели факторного анализа. Конкретная реализация этого подхода зависит от выбора варианта идентифицирующих условий типа 1)—3). Как правило, исследователю известна лишь ковариационная матрица  (или ее выборочное значение , пока мы их различать не будем).

Логическая схема итераций следующая:

во-первых, задаемся некоторым нулевым приближением V⁽⁰⁾ мат рицы V;

во-вторых, используя (4.21), получаем нулевое приближение ⁽⁰⁾ =  - V⁽⁰⁾ матрицы =QQ'=- V;

в-третьих, по  с помощью некоторого специального приема (см. ниже) последовательно определяем нулевые приближения q₁⁽⁰⁾, q₂⁽⁰⁾,.. q₂⁽⁰⁾ для столбцов q₁,q_2…,q_p' матрицы Q.

Затем определяем следующее (первое) приближение V⁽¹⁾ и т. д

Что касается специального приема определения столбцов q_i (i = 1,2,..., p') матрицы Q при известной матрице = QQ', то он опирается на тот факт, что матрица  может быть представлена в виде

=q₁ q₁’+ q₂ q₂’+ q_p’ q_p’’

Используя специфику выбранных идентифицирующих условий определяют вначале столбец q₁. Затем переходят к матрице ₁= — q₁ q₁’= q₂ q₂’+ ... + q_p’ q_p’’и определяют столбец q₂ и т. д.

Так, например, в случае «обобщенного условия треугольности» 3) этот прием даст:

D=B’Q-( d_1, d_2,… d_p’)

здесь d_i— i-й столбец матрицы D;

B=QQ'B-QD'=q₁d₁'+ ... + q_p'd'_p', B'B=B'QQ'B=DD' -d₁d₁'+... +d_p'd'_p'.

Последние два матричных уравнения можно расписать в виде:

b_i’= q₁d_i1+… + q_id_ii, (i = 1,2…p’)

b_i’b_i=d_j1d_i1+… d_jjd_ij (j<=i, i = 1,2…p’)

Отсюда можно последовательно находить

d₁₁²= b₁’b₁, ₁= — q₁ q₁’, q₂= (4.26)

q₁=, d₂₂²= b₂’₁b, ₂= — q₂ q₂’

В случае условий идентификации типа 1) легко проверить, что столбцы q₁,...q_p' являются первыми р' обобщенными собственными векторами (в метрике V) матрицы , т. е. являются решением уравнения

q_i -_iV q_i =0 (i=1, ...,p'), (4.27)

где i — i-й по величине характеристический корень уравнения

-V=0. (4.27')

Поэтому общая итерационная схема определения структуры модели реализуется здесь в такой последовательности: V⁽⁰⁾  ⁽⁰⁾ = - V⁽⁰⁾  q⁽⁰⁾ — решение уравнений (4.27) ⁽¹⁾ = Q⁽⁰⁾ Q^(0)' V⁽¹⁾ =  - ⁽¹⁾Q⁽¹⁾ — решение уравнений (4.27) и т. д.

Аналогичная реализация общей итерационной схемы определения

структуры модели имеет место и в случае условий идентификации типа (2), с той только разницей, что уравнения (4.27) и (4.27') следует заменить уравнениями

q_i -_i q_i =0 (i=1, ...,p'). (4.28)

-I=0

в) Статистическое оценивание факторных нагрузок q_ij и остаточных дисперсий v_ij. Оценивание производится либо методом максимального правдоподобия (см. § 1 главы 1), либо так называемым центроидным методом. Первый метод используется обычно при идентифицирующих условиях типа 1) и 2), хотя дает эффективные оценки для qij и vij, но требует постулирования закона распределения исследуемых величин (разработан он лишь в нормальном случае), а также весьма обременительных вычислений. Что касается центроидного метода, который используется при идентифицирующих условиях типа 3), то, давая оценки, близкие к оценкам максимального правдоподобия, он, как и всякий непараметрический метод, является более «устойчивым по отношению к отклонениям от нормальности исследуемых признаков и требует меньшего объема вычислений. Однако из-за определенного произвола в его процедуре, которая вскоре будет приведена, статистическая оценка метода, исследование его выборочных свойств (в общем случае) практически невозможно. Можно представить себе проведение подобных исследований лишь в каких-то специальных случаях, один из которых намечен, например, в [16].

Общая схема реализации метода максимального правдоподобия следующая. Составляется логарифмическая функция правдоподобия, как функция неизвестных параметров q_ij и v_ij, отвечающая исследуемой модели, т.е., учитывающая нормальность Х₁, ... , Хп, модель (4.20) и соответственно (4,21); дополнительные идентифицирующие условия 1) или 2). С помощью дифференцирования этой функции правдоподобия по каждому из неизвестных параметров и приравнивания полученных частных производных к нулю получается система уравнений, в которой известными величинами являются выборочные ковариации ^_ij, , а также числа р и р', а неизвестными — искомые параметры q_ij и v_ij . И, наконец, предлагается вычислительная (как правило, итерационная) процедура решения этой системы. За подробностями мы отсылаем читателя к [9], [22] и [16]. Заметим, что реализация описанной выше (для случаев 1) и 2)) обшей итерационной вычислительной схемы с заменой неизвестной ковариационной матрицы исходных признаков  ее выборочным аналогом ^ приведет нас как раз к оценкам максимального правдоподобия параметров q_ij v_ij (i=1,2 , ... , р; i = 1,2, ... , p'). Отметим также, что в [16] при достаточно общих ограничениях доказана асимптотическая нормальность оценок максимального правдоподобия Q^и V^ что дает основу для построения соответствующих интервальных оценок,

Как было отмечено, центроидный метод является одним из способов реализации вычислительной схемы (4.26), приспособленной для выявления структуры модели факторного анализа и оценки неизвестных параметров в случае идентифицирующих условий типа 3). Этот метод поддается весьма простой геометрической интерпретации. Отождествим исследуемые признаки х⁽¹⁾,., х^(р) с векторами, выходящими из начала координат некоторого вспомогательного р-мерного пространства, построенными таким образом, чтобы косинусы углов между х⁽ⁱ⁾и x^(j) равнялись бы их парным корреляциям (r_ij), а длины векторов х⁽ⁱ⁾ — стандартным отклонениям соответствующих переменных (_ij^1/2). Далее изменим на время, если необходимо, направления, т. е. знаки отельных векторов так, чтобы как можно больше корреляций стало положительными. Тогда векторы будут иметь тенденцию к группировке в одном направлении в пучок. После этого первый общий фактор y⁽¹⁾ определяется как нормированная (т. е. как вектор единичной длины) сумма всех исходных векторов пучка и, следовательно, он будет проходить каким-то образом через середину (центр) этого пучка; отсюда название «центроид» для общего фактора в этом случае.

Переходя затем к остаточным переменным, х⁽ⁱ¹⁾= x⁽ⁱ⁾—q_i1y⁽¹⁾, подпитывая ковариационную матрицу ⁽¹⁾ = — q₁q₁' для этих оста точных переменных и проделывая относительно х⁽ⁱ¹⁾ и ⁽¹⁾ всю ту же самую процедуру построения пучка и т. п., выделяем второй общий фактор («второй центроид») y⁽²⁾ и т. д.

Формализация этих соображений приводит к следующей итерационной схеме вычислений по определению факторных нагрузок q_ij, и остаточных дисперсий v_ij с учетом описанной ранее вычислительной схемы (4.26). Задаемся некоторым начальным приближением V⁽⁰⁾ для дисперсий остатков V. Обычно полагают [9, 42].

v_ii⁽⁰⁾=_ii^ [1- ].

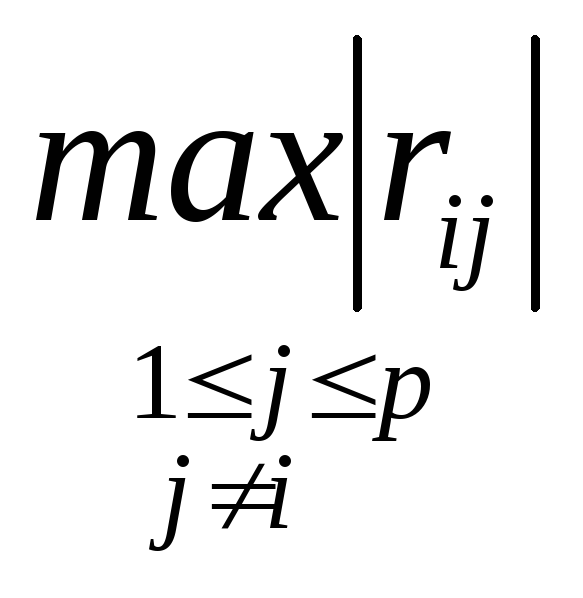Подсчитываем ⁽⁰⁾ =^ - V⁽⁰⁾. Выбираем в качестве нулевого приближения b₁⁽⁰⁾ первого столбца b₁ вспомогательной матрицы В столбец, состоящий из одних единиц

b₁⁽⁰⁾=

Далее в соответствии с (4.26) определяем нулевое приближение q₁⁽⁰⁾

первого столбца матрицы нагрузок

q₁⁽⁰⁾=

Затем вычисляется матрица ₁⁽⁰⁾ ⁽⁰⁾ - q₁⁽⁰⁾ q₁⁽⁰⁾' определяется нулевое приближение q₂⁽⁰⁾ второго столбца матрицы нагрузок

q₂⁽⁰⁾= , (4.29)

где вектор b₂⁽⁰⁾состоит только из + 1 или —1, а знаки подбираются из условия максимизации знаменателя правой части (4.29) и т, д. Получив, таким образом, нулевое приближение Q⁽⁰⁾ = (q(⁰⁾, ...q_p'⁽⁰⁾) для матрицы нагрузок Q, вычисляем V⁽¹⁾ = —Q⁽⁰⁾Q⁽⁰⁾' и переходим к следующей итерации. При этом матрица B⁽¹⁾не обязана совпадать с В⁽⁰⁾. Кстати, как нетрудно усмотреть из вышесказанного, i-й столбец мат рицы В задает веса, с которыми суммируются векторы одного пучка для образования i-го общего фактора («центроида»). Поскольку смысл центроидной процедуры—в простом суммировании векторов пучка; она иногда так и называется — «процедура простого суммирования», то исследователю остается определить лишь нужное направление каждого из векторов пучка, т. е. знаки единиц, образующих столбцы bi.

Непосредственная ориентация (при подборе знаков у компонент вектора b_i) на максимизацию выражений

хотя и несколько сложнее реализуема, чем некоторые эвристические приемы, опирающиеся на анализ знаков элементов остаточных матриц _i-1 [9, стр. 41—40], но быстрее и надежнее приводит к выделению именно таких центроидов, которые при заданном р' будут обусловливать возможно большую часть общей дисперсии исходных признаков, т. е. минимизировать дисперсию остаточных компонент и_i.

Заметим что если не все исходные ковариации _ij, положительны, может быть целесообразным использование и в качестве b_i⁽⁰⁾вектора, состоящего как из +1так и из —1. Отметим также, что недостатком центроидного метода является зависимость центроидных нагрузок q_ij от шкалы, в которой измерены исходные признаки. Поэтому исходные признаки x⁽ⁱ⁾ обычно нормируют с помощью среднеквадратических отклонений _ij^1/2так что выборочная ковариационная матрица ^ заменяется во всех рассуждениях выборочной корреляционной матрицей R^.

Анализируя описанную выше процедуру центроидного метода, не трудно понять, что построенные таким способом общие факторы могут интерпретироваться как первые р' «условных» главных компонент матрицы ^— V, найденные при дополнительном условии, что компоненты соответствующих собственных векторов могут принимать лишь два значения: плюс или минус единица.

г) Оценка значений общих факторов. Эта задача является одной из основных задач исследования. Действительно, мало установить лишь сам факт существования небольшого числа скрыто действующих общих факторов y⁽¹⁾,...,y^(p'), объясняющих природу взаимной коррелированности исходных признаков в основную часть их дисперсии. Желательно непосредственно «выловить» эти общие факторы, описать их в терминах исходных признаков и постараться дать им удобную содержательную интерпретацию.

Мы приведем здесь идеи и результаты двух распространенных методов решения этой задачи, предложенных в разное время Бартлеттом (1938 г.) и Томсоном (1951 г.). В обоих случаях мы предполагаем за дачу статистического оценивания неизвестных нагрузок Q' ~= (q_ij^) и

остаточных дисперсий V~ = (v_ij^) уже решенной.

Первый метод (метод Бартлетта) рассматривает отдельно для каждого фиксированного номера наблюдения v (v = 1, 2, ..., n) модель (4.20) как регрессию признака Хv по аргументам q_.1^, q_.2^, ..., q_.p’^, при этом верхний индекс i = 1, 2, ..., р у признака (и соответствующий первый нижний индекс у нагрузок) играет в данном случае роль номера наблюдений в этой регрессионной схеме, так что

x_v⁽ⁱ⁾=, (i=1,..p)

Таким образом, величины y_v⁽¹⁾,.. y_v^(p’) интерпретируются как неизвестные коэффициенты регрессии x_v. по q_.1^, q_.2^, ..., q_.p’^. В соответствии с известной техникой метода наименьших квадратов (с учетом неравноточности» измерений, т. е. того факта, что вообще говоря Dx ⁽ⁱ¹⁾ Dx ⁽ⁱ²⁾ при i1i2), определяющей неизвестные коэффициенты регрессии Yv ^= (у_v⁽¹⁾^, , )' из условия

=

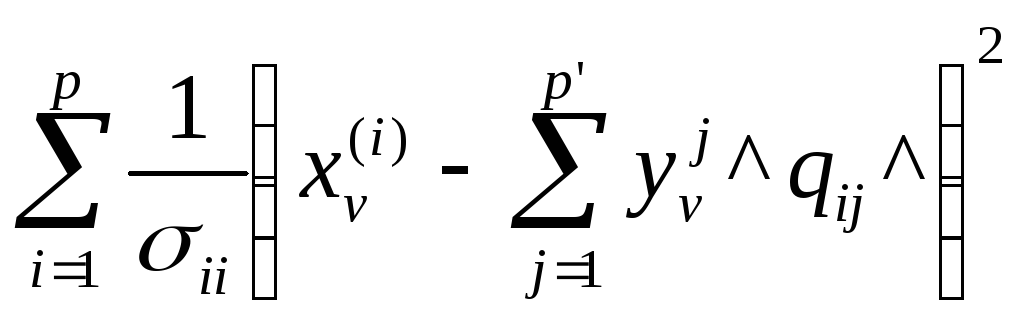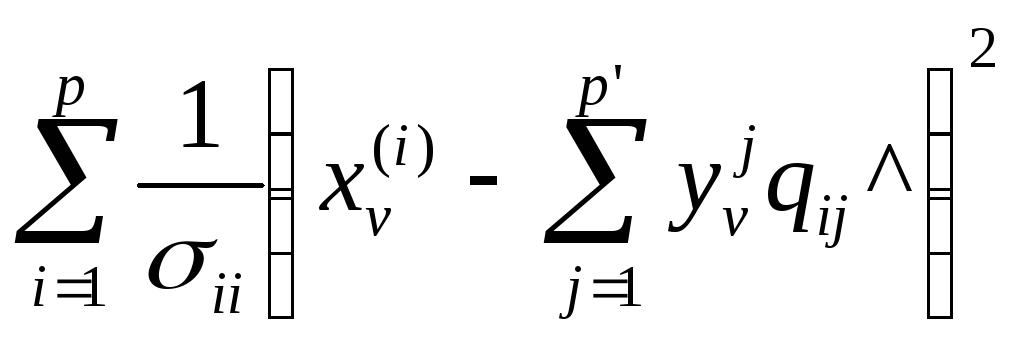
получаем [2]

, (v=1,..,n) (4.30)

Очевидно, если исследуемый вектор наблюдений Х нормален, то эти оценки являются одновременно и оценками максимального правдоподобия. Нестрогость данного метода — в замене истинных (неизвестных нам) величин q_ij и v_ij их приближенными (оценочными) значениями qij^ и vij^

Второй метод (метод Томсона) рассматривает модель (4.20) как бы «вывернутой наизнанку», а именно как регрессию зависимых переменных y⁽¹⁾,...,y^(p') по аргументам х⁽¹⁾, .... х^(p). Тогда коэффициенты с_ij^ в соотношениях

, (I =1..p)

или в матричной записи

У^= СХ,

где С — матрица коэффициентов сij размера р'  р, находятся в соответствии с методом наименьших квадратов из условия

=

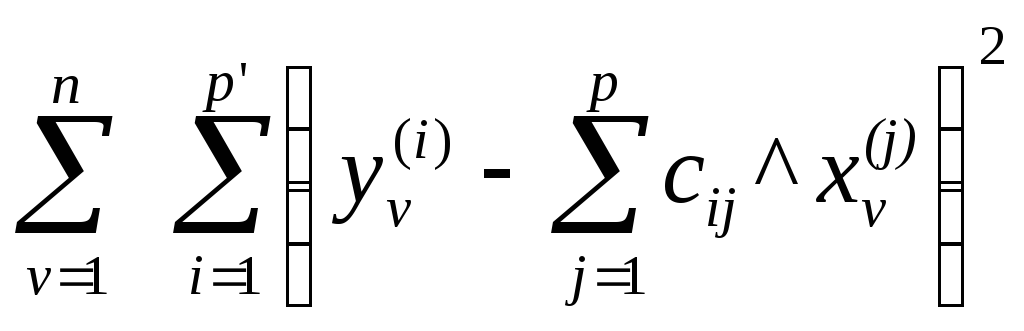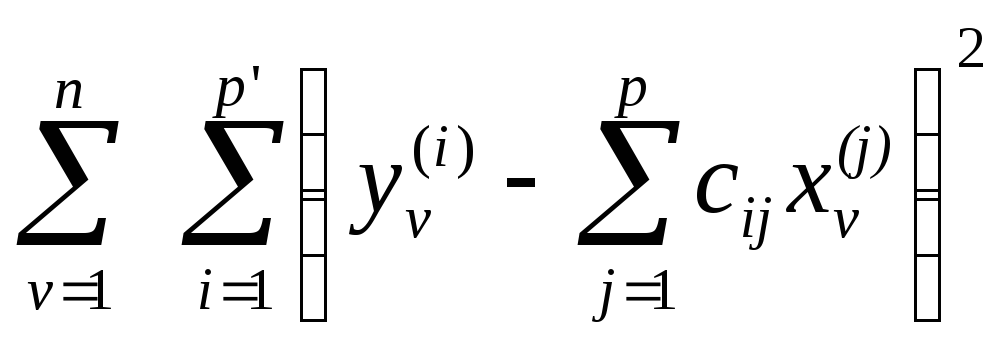
(4.31)

Поскольку решение экстремальной задачи (4.31) выписывается, как известно [21, в терминах ковариации х⁽ⁱ⁾ и y⁽ⁱ⁾, то отсутствие наблюдений по зависимым переменным y(i) можно компенсировать знанием этих ковариации, так как легко подсчитать, что

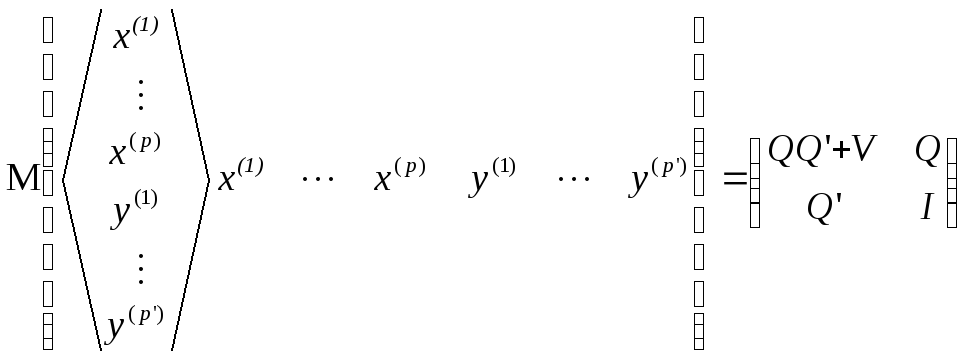
Отсюда, используя известные формулы метода наименьших квадратов, получаем (с заменой матрицы Q, V и Г их выборочными аналогами)

(v=l,2,..,n), (4.32)

где матрица Г (размера р  р) определяется соотношением

Г= Q^'V^^-1Q^,

Сравнение выражений (4.30) и (4.32) позволяет получить явное соотношение между решением по методу Бартлетта Y^^(Б) и решением, .предложенным Томсоном Y^^(T).

Y^(Б)=(I+Г-1) Y^(T)

Если элементы матрицы Q^'V^^-1Q^ достаточно велики, то эти два метода будут давать близкие решения,

д) Статистическая проверка гипотез. Проверка гипотез, связанных с природой и параметрами используемой модели факторного анализа, составляет один из необходимых элементов исследования. К сожалению, теория статистических критериев применительно к моделям торного анализа разработана весьма слабо. Пока удалось построить лишь так называемые критерии адекватности модели, т. е. критерии, предназначенные для проверки гипотез типа гипотезы Но, заключающейся в том, что исследуемый вектор наблюдений Х допускает представление с помощью модели факторного анализа (4.20) с данным (заранее выбранным) числом общих факторов р'. При этом критическая статистика ₁(Х₁, .... Х_n), т. е. функция от результатов наблюдения, по значению которой принимается решение об отклонении или непротиворечивости высказанной гипотезы Н₀, зависит от вида дополнительных (идентифицирующих) условий модели. Так, если рассматривается модель с дополнительными идентифицирующими условиями вида 1), т. е. дополнительно постулируется диагональность матрицы Г = Q'^V^^-1Q^, то гипотеза Hо отвергается (с вероятностью ошибиться, приблизительно равной ) в случае

₁(Х₁, .... Х_n)=n (ln V^ + ln I+Г -ln ^)>²_(v₁),

где число степеней свободы

v₁=[(p-p’)²-(p+p’)],

его положительность обеспечивается условием (4.25), а ²_(v₁), как и ранее величина 100  %-ной точки-² -распределения с v₁, степенями свободы (находится из таблиц).

На языке ковариационных матриц гипотеза Н₀ означает в данном случае, что элементы матрицы ^ - (Q^Q'^ + V^) должны лишь статистически незначимо отличаться от нуля, или, что эквивалентно, матрицы ^ - V^ должна иметь ранг, равный р'. А это, в свою очередь, означает что последние р—р' характеристических корней 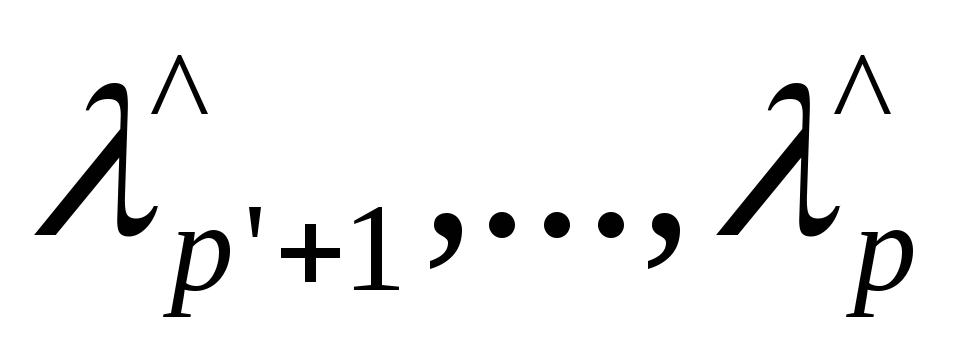уpaвнения ^—V—V^=0 должны лишь незначимо отличаться от нуля. Кстати, статистика

₁(Х₁, .... Х_n)может быть записана в терминах этих характеристических корней, а именно

₁(Х₁, .... Х_n)=n

Если же в качестве идентифицирующих условий дополнительно к (4.20), или, что то же, к (4.21), постулируется наличие какого-то заранее заданного числа m нулевых нагрузок q_ij из общего числа р•р' на определенных («специфических») позициях, то гипотеза H₀ отвергается (с вероятностью ошибиться, приблизительно равной ) в случае

₂(Х₁, .... Х_n)= n(lnV^+lnQ^’V^-1^^V^-1Q^-lnГ-ln^)>²_(v₃),

где число степеней свободы

v2=p(p-1)-(pp'-m)

Иногда удобнее вычислять критическую статистику ₂(Х₁, .... Х_n) в терминах характеристических корней z₁^, ...,z_p^ (занумерованных в порядке убывания их величин) выборочной корреляционной матрицы R^ исследуемого вектора наблюдений X:

₂(Х₁, .... Х_n)=

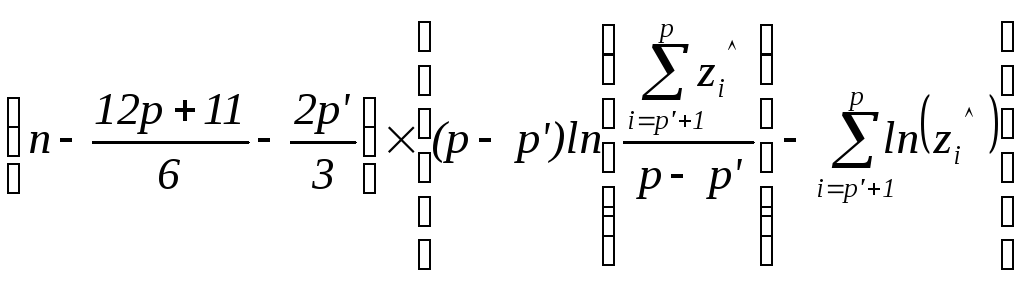
Статистики ₁(Х₁, .... Х_n) и ₂(Х₁, .... Х_n) получены в результате реализации известной схемы критерия отношения правдоподобия.

Пользуясь этой схемой, можно построить аналогичные критерии адекватности и для некоторых специальных вариантов центроидного метода [9, с. 50]. Однако из-за слишком узких рамок такой модели эти критерии, с нашей точки зрения, не представляют достаточного интереса.

Д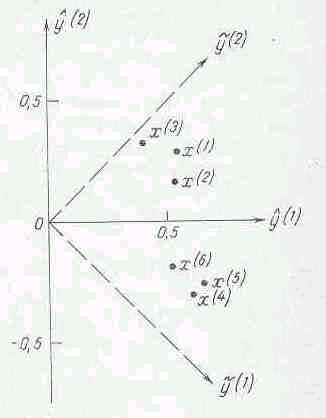о сих пор не удалось построить многомерной решающей процедуры типа р' (2), т. е. оценки для неизвестного числа общих факторов р'. В настоящее время приходится ограничиваться последовательной эксплуатацией критериев адекватности Н₀ : р' = р₀ (р'₀ — заранее задано) при альтернативе H₁: р'>p'₀) Если гипотеза Но отвергается, то переходят к проверке гипотезы Н₀ : р' = р'₀ + 1 при альтернативе Н₁': р'>р₀+1 и т. д. Однако по уровням значимости  каждой от дельной стадии такой процедуры трудно сколько-нибудь точно судить о свойствах всей последовательной процедуры в целом.

В последних двух столбцах таблицы даны факторные нагрузки q_i1 q_i2 на исследуемые признаки в бифакторной модели (p' = 2), подсчитанные по приведенной здесь корреляционной матрице с помощью центроидного метода. Простой анализ величин и знаков этих нагрузок склоняет нас к тому, чтобы интерпретировать первый фактор y⁽¹⁾ как фактор общей одаренности, а второй фактор y⁽²⁾ как фактор гуманитарной одаренности.

Рис.4.7. Изображение исходных признаков х(1),...,х(6) в плоскости двух общих факторов у^⁽¹⁾ 0 у^⁽¹⁾

В прямой постановке задачи классификации (т. е. при классификации обследованных учащихся) исследователь должен был бы, в первую очередь, определить, как эти два общие фактора у^⁽¹⁾ и у^⁽²⁾ выражаются через исходные признаки x⁽¹⁾,..x⁽⁶⁾; затем подсчитать значения (у^_v⁽¹⁾, у^_v⁽²⁾) (v = 1, 2, ..., 220) этих двух факторов для каждого из обследованных учеников и, наконец, нанести 220 точек (у^_v⁽¹⁾, у^_v⁽²⁾) на плоскость у^⁽¹⁾ 0 у^⁽²⁾. Расположение «точек-учеников» на плоскости

позволило бы исследователю получить ряд вспомогательных сведений, полезных при

формулировке окончательных выводов (наличие четко выраженных «сгущений точек» — классов, их число, их интерпретация и т. п.)². Кстати, метод Томсона (l.32) дает в качестве оценки общих факторов выражения:

у^⁽¹⁾=0,245х⁽¹⁾+0,208x⁽²⁾+ 0,158х⁽³⁾ + 0,278х⁽⁴⁾+ 0,271х⁽⁵⁾ +0,157х⁽⁶⁾,

у^⁽²⁾=0,352х⁽¹⁾+0,201x⁽²⁾ +0,309x⁽³⁾-0,351x⁽⁴⁾ -0,303x^{(5) -} 0,126х⁽⁶⁾.

При обратной (двойственной) постановке задачи, т.е. при классификации исследуемых признаков х⁽¹⁾,х⁽²⁾,...,х⁽⁶⁾, оказывается полезной следующая геометрическая интерпретация общих факторов и исходных признаков.

Рассмотрим рис.4.7, на котором осями координат являются общие факторы y⁽¹⁾ и у⁽²⁾, а координаты точек (у^_i⁽¹⁾,у_i^⁽²⁾) =(q_i1, q_i2 ) определяются нагрузками 1-го исходного признака на общие факторы (i = 1, 2, .... 6). Соответственно точку (q_i1, q_i2) удобно интерпретировать как изображение i-го исходного признака x⁽ⁱ⁾. Расположение точек на рис. 4.7 свидетельствует о естественном распадении совокупности исходных признаков на две группы: группу гуманитарных признаков (х⁽¹⁾, х⁽²⁾, x⁽³⁾) и группу математических признаков (x⁽⁴⁾, x⁽⁵⁾, x⁽⁶⁾).

Кстати, подобная геометрическая интерпретация помогает выбрать вращение системы общих факторов, наиболее подходящее с точки зрения возможности их содержательной интерпретации. Дело в том, что как мы уже отмечали параметры модели факторного анализа, в том числе и сами общие факторы у⁽¹⁾, у⁽²⁾, ..., у^(p'), определяются не однозначно, а лишь с точностью до некоторого ортогонального преобразования, т. е. с точностью до вращения осей у⁽¹⁾, у⁽²⁾, ..., у^(p') в пространстве. При этом выбор окончательного решения, т. е. закрепление системы у⁽¹⁾, у⁽²⁾, ..., у^(p') в определенном положении, находится в распоряжении исследователя. Другими словами, исследователь должен решить вопрос: как, располагая некоторым частным решением у⁽¹⁾, у⁽²⁾, ..., у^(p'), полученным, например, с помощью центроидного метода, выбрать такое ортогональное преобразование, такой поворот осей у^(1)~, у⁽²⁾, ..., у^(p'), при котором получаемые при этом новые общие факторы у^(1)~ у^(2)~ ..., у^(p')~ допускают наиболее естественную н убедительную содержательную интерпретацию. Рассматривая расположение исходных признаков в плоскости у⁽¹⁾0у⁽²⁾или в пространстве, натянутом на первые три общих фактора, естественно повернуть координатную систему таким образом, чтобы координатные оси прошли через наиболее четко выраженные сгущения точек-признаков (см.поворот, намеченный пунктирными осями у^(1)~ и у^(2)~ на рис. 4,7). При этом иногда бывает полезно отказаться от ортогональности общих факторов, переходя к косоугольной системе координат.