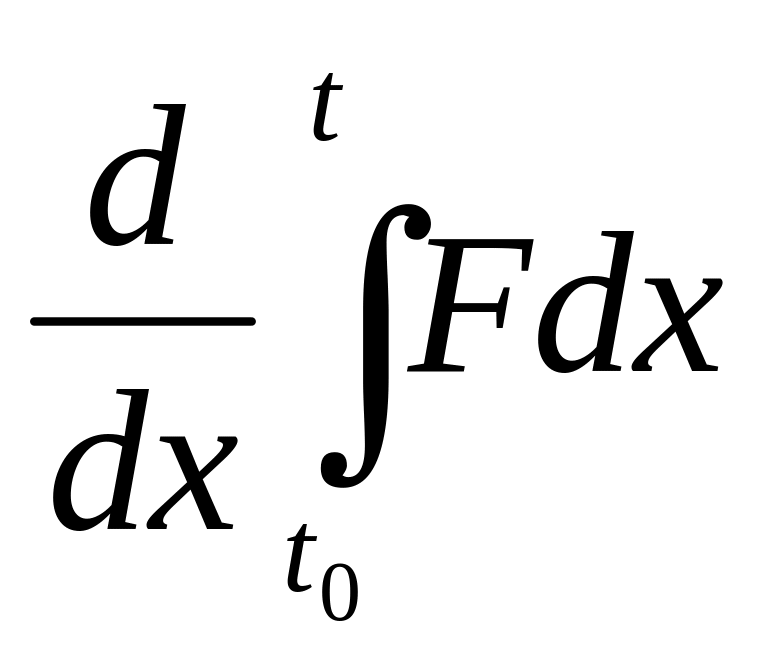- •Contents
- •Передмова
- •We are students at donetsk national university
- •Vocabulary
- •1. Guess the meaning of these international words. Check with your teacher or a dictionary
- •2. Key words
- •Student Dima Loboda
- •Student Dasha Klimova
- •Student Nastya Savchuk
- •Student profile
- •L earn mathematics in English Cardinal and ordinal numbers
- •1. Read the text about two arithmetical operations and do the exercises that follow it Basic arithmetical operations. (Addition & subtraction)
- •What’s your best friend like?
- •Vocabulary
- •1. Guess the meaning of these international words. Check with your teacher or a dictionary
- •2. Key words
- •Who’s their ideal partner?
- •L earn mathematics in English
- •1. Read the text and do the exercises below it Basic arithmetical operations (Multiplication & division)
- •A day in the life of a student
- •Vocabulary
- •1. Guess the meaning of these international words. Check with your teacher or a dictionary
- •2. Key words
- •I. Look through the text and do the tasks
- •Learn mathematics in English
- •I. Read the text and do the exercises below it. Advanced arithmetical operations
- •What’s your university like?
- •Vocabulary
- •1. Guess the meaning of these international words. Check with your teacher or a dictionary
- •2. Key words:
- •Donetsk national university
- •The University of Sheffield
- •1. Find a partner from the other group. Tell each other the information you read about one of the universities
- •Fractions
- •The city I live and study in
- •Vocabulary
- •1. Guess the meaning of these international words. Check with your teacher or a dictionary
- •2. Key words:
- •Learn mathematics in English
- •Mixed numbers
- •Mathematics is the queen of scienses
- •Vocabulary
- •1. Guess the meaning of these international words. Check with your teacher or a dictionary
- •Key words:
- •“`A mathematician is a machine for converting coffee into theorems”. /Paul Erdos/
- •L earn mathematics in English
- •Equivalent fractions
- •Reciprocals and the "invisible denominator"
- •The language of mathematics
- •Vocabulary
- •1. Guess the meaning of these international words. Check with your teacher or a dictionary
- •Key words
- •L earn mathematics in English
- •Statistics is very serious!
- •Vocabulary
- •1. Guess the meaning of these international words. Check with your teacher or a dictionary
- •Key words:
- •Statistics is very serious!
- •Get to know a typical computer
- •Vocabulary
- •1. Guess the meaning of these international words. Check with your teacher or a dictionary
- •2. Key words:
- •Get to know a typical computer
- •Computer without a program is just a heap of metal!
- •Vocabulary
- •1. Guess the meaning of these international words. Check with your teacher or a dictionary.
- •2. Key words
- •We can’t imagine modern computing without them
- •Vocabulary
- •1. Guess the meaning of these international words. Check with your teacher or a dictionary
- •2. Key words
- •I. Read the following texts and do the tasks Alan Turing
- •Tim Berners-Lee
- •He has left mathematicians enough to keep them busy for five hundred years
- •Vocabulary
- •1. Guess the meaning of these international words. Check with your teacher or a dictionary.
- •2. Key words
- •I. Read the text and do the tasks niels henric abel
- •Getting to know each other better
- •II. Swap charts with b. Ask a to explain the information in his/her chart. Ask for more information
- •III. Explain your answers to b
- •Mood graph
- •A time for everything
- •Expert opinion
- •Vocabulary
- •Vocabulary
- •What’s your body age?
- •I. Read the questionnaire and answer the questions below, adding or subtracting the numbers after your answer from your actual age
- •How many friends can you share problems with?
- •15. Have you taken antibiotics in the past five years?
- •II. Check your score
- •If you're younger than your years
- •I. Look at your partner’s answers. Ask for more information, for example: What is your worst diet habit? How much time do you have for yourself?
- •II. Some ways to lower our body age are given below. Read it and give your partner some good advice starting with the following words: I think you should…
- •Donetsk national university
- •Inspires students’ enthusiasm for learning
- •An ideal teacher
- •Is a well-educated person has a good sense of humor is a polite and a punctual person delivers interesting lectures
- •Numbers
- •I. Mind–map’ numbers’. When you read this ‘mind-map’, you’ll meet words that are new to you. First try to guess their meaning and then look them up in a dictionary.
- •II. Answering and explaining
- •III. Playing a trick with numbers
- •IV. The ‘Terribly Stressed‘ game
- •I. Use this mind-map ‘Four basic operations in Mathematics’ as a topic activator to speak about the basic operations in Arithmetic
- •III. Reading, writing and saying numerical expressions
- •3. Look at each numerical expression written in symbols and signs. Then say it in words. Your partner will listen to see if you repeat correctly and correct your incorrect answers
- •I. Use this mind-map ‘Algebra’ as a topic activator to speak about Algebra (its origin and some facts from its history)
- •II. Match each numerical expression in the left column with the equivalent expression in the right column
- •Look at the expressions written in words and write them in mathematical notation (in symbols)
- •III. Read the following inequalities aloud. Your partner will check your answers
- •I. Mind-map ‘Geometry’. Use this map to speak about geometry (its meaning, the history of its development, its application). Add more information you know
- •II. Working with geometric terms. Demonstrate your knowledge of geometric terms. Work in pairs (a/b)
- •The language of mathematics
- •Practice set 12
- •III. Draw your mood graph or graph with your marks showing changes during the week or a month (semester). Explain it to your partner
- •Some facts from the history of mathematics education
- •I. Read the article and mark the sentences t (true), f (false) or ng (not given)
- •Do you know that…
- •II. Search for some information about one of these mathematics teachers and share it with other students. Make a table of the most important facts of his/her biography
- •Ancient sources of information
- •I. Choose from (a-j) the one which best fits each of (1-7). There are two choices you do not need to use.
- •II. Tell your partner about these famous papyri
- •III. Find some information about Mathematics of ancient civilizations and share it with other students (e.G. The Maya calendar, the ancient numeration systems)
- •The history of the symbols for plus and minus
- •I. Read the article. Guess the meaning of the highlighted words. Check with the teacher or your dictionary
- •II. Read the article again. Say what events the following years refer to:
- •III. Tick (√) the things the article says
- •IV. Read the facts listed below. In pairs, discuss which one is the most surprising do you know that...
- •V. Find some information on the history of the mathematical symbols. Give a presentation to the students of your group
- •Statistics
- •I. Match the words with their definitions:
- •II. Decide if the given statements are true (t) or false (f) according to the text
- •III. Search for information about one of the scientists listed below and then give a presentation
- •Important contributors to statistics
- •Degrees and diplomas in statistics
- •III. Do you know anything about awards in Statistics in your country or abroad?
- •Why is there no nobel prize in mathematics?
- •I. Read the text. Seven sentences have been removed from it. Choose from the choices (a- I) the one which fits each gap (1-7). There are two choices you do not need to use
- •III. Work in pairs. Tell your partner why Nobel decided against a Nobel Prize in mathematics
- •Major awards in mathematics
- •The obverse of the Fields Medal
- •The reverse of the Fields Medal
- •A. Fields medal
- •III. Look at these words. Why are they important in this text?
- •B. Abel prize
- •IV. Focus on these words. Why are they important in the text?
- •VI. Compare the major awards in Mathematics with the Nobel Prize by using like (similar to) or unlike (different from) in the sentences
- •V. Search for more information on the following topics on the Internet and share it with other students
- •Abel Prize Laureates
- •Fields medalist
- •I. Decide if the given statement is true (t) according to the text, if it is false (f) or if the information is not given (ng) in the text (Work in pairs)
- •II. Number these events in the order they happened. Look at the Reading
- •III. Interview your partner about this great mathematician (Work in pairs)
- •IV. Ask and answer the following questions in pairs
- •II. Match the number with its symbolic meaning:
- •III. Answer the questions below and then ask for more information (Work in pairs)
- •Do you know that…
- •IV. Find information on the Internet and give a presentation of the number you are interested in (brings you good or bad luck)
- •Text 10
- •Reading and Speaking
- •Number and reality
- •I. Match the word with its meaning:
- •II. Work in pairs. Decide if the sentences 1- 7 are t (true) or f (false)
- •A strong mathematical component
- •I. Choose from (a-j) the one which best fits each of (1-6). There is one choice you do not need to use
- •II. Match choices (a-d) to (1-4)
- •III. In pairs, find and then say what events the following years refer to:
- •IV. Do you know an artist (a writer) having a strong mathematical component in his/her creative work? Search for information on the Internet and give a presentation on the subject
- •Reading and Speaking fractal
- •I. Match the words with their meanings:
- •II. Choose from (a-f) the one which best fits each of (1-5). There is one choice you do not need to use
- •III. Work in pairs. Tell your partner about fractal
- •IV. On the Internet search for information about applications of fractals and then share your information with other students
- •Healthy computer work
- •Match the words with their meanings:
- •I I. Read the article once and then decide if the following guidelines are true, false or are not mentioned in the text above
- •III. Team work. Work out the main rules for operating the computer. The winner is to give clear recommendations for young people working on the computer. The first one is given for you
- •IV. Ask and answer the questions (Work in pairs)
- •Computers can do wonders
- •I. Match the words with their meanings
- •II. Decide if the following statements are true or false (t/f) by referring to the information in the text
- •III. Work in pairs. Tell your partner about the most surprising facts from the article
- •IV. Search for information about ‘computer wonders’ on the Internet and give a presentation about new computer developments (e.G. Robots)
- •Watching ‘how did mathematics begin? (a cartoon)
- •I. Answer the following questions:
- •II. Tell the class about the most interesting facts you have learned from the cartoon. Do you agree with the information mentioned in the cartoon? Add more information about the development of numbers
- •Recommendations and some useful phrases for giving presentations
- •Introduction
- •Introducing your subject
- •If you make a mistake, start your sentence again.
- •If you can’t remember a word, use another one.
- •Conclusion
- •Inviting questions
- •Questions
- •Wording mathematical signs, symbols and formulae
- •Answer keys
- •References
Questions
Questions are a good opportunity for you to interact with your audience. It may be helpful for you to try to predict what questions will be asked so that you can prepare your response in advance. You may wish to accept questions at any time during your presentation, or to keep a time for questions after your presentation. Normally, it's your decision, and you should make it clear during the introduction. Be polite with all questioners, even if they ask difficult questions. They are showing interest in what you have to say and they deserve attention. Sometimes you can reformulate a question or answer the question with another question, or even ask for comment from the rest of the audience.
Appendix B
Wording mathematical signs, symbols and formulae
|
Plus |
- |
Minus |
|
plus or minus |
|
sign of multiplication; multiplication sign |
|
sign of division; division sign |
|
round brackets; parentheses |
|
Curly brackets; braces |
|
square brackets; brackets |
|
Therefore |
|
approaches; is approximately equal |
~ |
equivalent, similar; of the order of |
|
is congruent to; is isomorphic to |
|
a equal b; a is equal to b |
|
a is not equal to b; a is not b |
|
approximately equals b |
|
a plus or minus b |
|
a is greater than b |
|
a is substantially greater than b |
|
a is less than b |
|
a is substantially less than b |
|
a second is greater than a d-th |
|
x approaches infinity x tends to infinity |
|
a is greater than or equals b |
|
p is identically equal to q |
|
n factorial |
|
Laplacian |
|
a prime |
|
a double prime; a second prime |
|
a triple prime |
|
a vector; the mean value of a |
|
the first derivative |
|
a third; a sub three; a suffix three |
|
a j th; a sub j product |
|
f prime sub (suffix) c; f suffix (sub) c, prime |
|
a second, double prime; a double prime, second |
|
eighty seven degrees six minutes ten second |
|
a plus b is c; a plus b equals c; a plus b is equal to c; a plus b makes c |
|
a plus b all squared |
|
c minus b is a; c minus b equals a; c minus b is equal to a; c minus b leaves a |
|
bracket two x minus y close the bracket |
|
a time b is c; a multiplied by b equals c; a by b is equal to c |
|
a is equal to the ratio of e to l |
|
ab squared (divided) by b equals ab |
|
a divided by infinity is infinity small; a by infinity is equal to zero |
|
x plus or minus square root of x square minus y square all over y |
|
a divided by b is c; a by b equals c; a by b is equal to c; the ratio of a to b is c |
|
a to b is as c to d |
|
a (one) half |
|
a (one) third |
|
a (one) quarter; a (one) fourth |
|
two thirds |
|
twenty five fifty sevenths |
2 |
two and a half |
|
one two hundred and seventy third |
|
o [ou] point five; zero point five; nought point five; point five; one half |
|
o [ou] point five noughts one |
|
the cube root of twenty seven is three |
|
the cube root of a |
|
the fourth root of sixteen is two |
|
the fifth root of a square |
|
Alpha equals the square root of capital R square plus x square |
|
the square root of b first plus capital A divided by two xa double prime |
|
a) dz over dx b) the first derivative of z with respect to x |
|
a) the second derivative of y with respect to x b) d two y over d x square |
|
the nth derivative of y with respect to x |
|
partial
d two z over partial dsquare plus partial d two z over partial d |
|
y is a function of x |
|
d over dx of the integral from t nought to t of capital F dx |
|
capital E is equal to the ratio of capital P divided by a to e divided by l is equal to the ratio of the product Pl to the product ae |
|
capital L equals the square root out of capital R square plus minus square |
|
gamma is equal to the ratio of c prime c to ac prime |
|
a to the m by nth power equals the nth root of (out of) a to the mth power |
|
the integral of dy divided by the square root out of c square minus y square |
|
capital F equals capital C sub (suffix) mu HIL sine theta |
|
a plus b over a minus b is equal to c plus d over c minus d |
|
capital V equals u square root of sine square i plus cosine square i equals u |
|
tangent r equals tangent i divided by l |
|
the decimal logarithm of ten equals one |
|
a cubed is equal to the logarithm of d to the base c |
|
four c plus W third plus two n first a prime plus capital R nth equals thirty three and one third |
|
capital
P sub (suffix) cr (critical) equals |
|
x + a is round brackets to the power p minus the r-th root of x all (in square brackets) to the minus q-th power minus s equals zero |
|
Open round brackets capital D minus r first close the round brackets open square and round brackets capital D minus r second close round brackets by y close square brackets equals open round brackets capital D minus r second close the round brackets open square and round brackets capital D minus r first close round brackets by y close square brackets |
|
u is equal to the integral of f sub one of x multiplied by dx plus the integral of f sub two of y multiplied by dy |
|
capital M is equal to capital R sub one multiplied by x minus capital P sub one round brackets opened x minus a sub one brackets closed minus capital P sub two round brackets opened x minus a sub two brackets closed |
|
a sub v is equal to m omega omega square alpha square divided by square brackets, r, p square m square plus capital R second round brackets opened capital R first plus omega square alpha square divided by rp round and square brackets closed |
|
a) |
|
the
absolute value of the quantity
sub j of t one minus
sub j of t two is less than or equal to the absolute value of the
quantity M of t one minus |
|
the
limit as s becomes infinite of the integral of f of s and |
|
sub
s plus l, times e to the power of t times |
|
the partial derivative of F of lambda sub i of t and t, with respect to lambda, multiplied by lambda sub i prime of t, plus the partial derivative of F with arguments lambda sub i of t and t, with respect to t, is equal to zero |
|
the second derivative of y with respect to s, plus y, times the quantity 1 plus b of s, is equal to zero |
|
f of z
is equal to infinite, with the argument of z equal to gamma |
|
D sub n minus 1 of is equal to the product from s equal to zero to n of, parenthesis, 1 minus x sub s squared, close parenthesis, to the power epsilon minus 1 |
|
the second partial (derivative) of u with respect to t plus a to the fourth power, times u, is equal to zero, where a is positive |
|
set of functions holomorphic in D (function spaces) |
|
Norm of f, the absolute value of f |
|
distance
between the sets |
|
b is the imaginary part of a + bi (complex variables) |
|
a is the real part of a + bi (complex variables) |
∂S |
the boundary of S |
|
the complement of S |
|
union of sets C and D |
|
intersection of sets C and D |
|
B is a subset of A; B is included in A |
|
a is an element of the set A; a belongs to A |