
- •42 Двоенко с.Д. Методы анализа бмд
- •2. Основы анализа связей
- •Предположение о природе связи
- •2.2. Нормальное распределение
- •2.3. Корреляционная матрица и ее основные свойства
- •2.4. Собственные векторы и собственные числа корреляционной матрицы
- •2.5. Приведение корреляционной матрицы к диагональной форме
- •2.6. Геометрическая интерпретация главных компонент на плоскости
- •2.7. Модель главных компонент
- •2.8. Приближенное вычисление собственных чисел и векторов корреляционной матрицы
- •Понятие об измерении связи между качественными признаками. Статистический подход
- •2.10. Теоретико-информационный подход
- •2.11. Проблема интерпретации значений коэффициентов связи
Понятие об измерении связи между качественными признаками. Статистический подход
Как мы уже знаем, качественные признаки возникают при измерениях свойств объектов, например, в номинальной или ранговой шкалах. Пусть два качественных признака измерены в однотипных шкалах. Часто возникает вопрос о существовании или отсутствии связи между ними. Такая ситуация типична, например, при обработке результатов анкетирования. Рассмотрим измерение связи в номинальной шкале.
Пусть N- число
наблюдений. Тогда, если в номинальной
шкале присутствуетr наименований,
тоNi- наблюденная частота
появленияi-го значения. Очевидно,
что![]() .
Тогда
.
Тогда![]() -
относительная частота
-
относительная частота
i-го
значения, где![]() .
.
Типичным является наглядное представление распределения объектов по группам в виде столбиковой диаграммы (гистограммы или полигона частот). В связи с таким представлением данных рассмотрим следующую статистическую задачу.
Пусть выдвинута гипотеза H о том, что Nизмерений некоторого признака есть выборкаNзначений случайной величины с некоторым законом распределения. Если гипотеза H справедлива, то дискретное распределение выборки можно считать статистической оценкой распределения всей генеральной совокупности. Из-за случайных колебаний эти два распределения не будут совпадать, но можно ожидать, что с ростомNраспределение выборки будет приближаться к распределению генеральной совокупности. Тогда следует ввести некоторую меру несовпадения распределений и изучить свойства ее выборочного распределения.
Такие меры несовпадения
можно конструировать различными
способами, но наиболее важной является
мера, основанная на критерии
![]() К.Пирсона.
К.Пирсона.
Пусть
![]() -
вероятности дискретных значений, где
-
вероятности дискретных значений, где![]() ,
образующие генеральный закон распределения
случайной величины. По методу наименьших
квадратов построим меру различия как
сумму квадратов отклонений наблюдаемых
частот от теоретических
,
образующие генеральный закон распределения
случайной величины. По методу наименьших
квадратов построим меру различия как
сумму квадратов отклонений наблюдаемых
частот от теоретических![]() ,
гдеci - произвольные
коэффициенты. К.Пирсон показал, что при
,
гдеci - произвольные
коэффициенты. К.Пирсон показал, что при![]() получается мера расхождения
получается мера расхождения
 ,
,
распределение которой при
![]() стремится к распределению
стремится к распределению![]() .
.
Вспомним данное
распределение. Пусть имеется rнезависимых нормальных случайных
величин![]() ,
,![]() .
Обозначим
.
Обозначим![]() ,
а плотность распределения данной суммы
как
,
а плотность распределения данной суммы
как![]() -
распределение
-
распределение
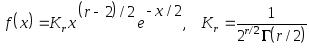 ,
,
где:
![]() - аргумент распределенияf(x);
- аргумент распределенияf(x);
Kr-
константа для выполнения условия
нормировки![]() ;
;
Г(n) - гамма-функция, где для целыхn>0 :
![]() и
и![]() ;
;
r- число степеней свободы.
Вид
![]() -
распределения полностью определяется
числомr, а приr>30 практически
переходит в нормальное
-
распределения полностью определяется
числомr, а приr>30 практически
переходит в нормальное![]() .
Для некоторыхrраспределение имеет
вид (рис. 2.2):
.
Для некоторыхrраспределение имеет
вид (рис. 2.2):
1
2 3 4 5 6x
 f(x)
r=1
f(x)
r=1
 0.5
0.5  r=2
r=2 0.4
0.4 r=3

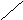 0.3
0.3
 r=
4
r=
4 0.2


0.1

 0
0![]()

 ,
,


Рис. 2.2. Распределение Пирсона.
Пусть
x=![]() -- значимое значение
-- значимое значение![]() сr-1 степенью свободы. Оно определяется
так, чтобы вероятность для наблюденного
значения
сr-1 степенью свободы. Оно определяется
так, чтобы вероятность для наблюденного
значения![]() превысить
превысить![]() равнялась величине
равнялась величине
 .
.
Пусть настолько
мало, что можно считать практически
достоверным, что при одном испытании
событие с вероятностью
не произойдет. Если гипотеза Н верна,
то практически невозможно в единственном
эксперименте получить значение![]() .
Если же это так, то мы должны признать
значимое отклонение от гипотезы Н и ее
отвергнуть.
.
Если же это так, то мы должны признать
значимое отклонение от гипотезы Н и ее
отвергнуть.
Вероятность ошибки
(отвергнута справедливая гипотеза Н)
есть вероятность
![]() .
Это так называемая ошибка первого рода.
.
Это так называемая ошибка первого рода.
Измерим связь между
двумя признаками. Статистическая
интерпретация силы связи номинальных
признаков основана на критерии
![]() .
Пусть даны два таких признака и построены
их гистограммы, не обязательно графически,
а, например, в виде числового ряда.
Совместное распределениеNнаблюдений
одновременно поrзначениям первого
признакаX и поsзначениям
второго признакаYобразуют таблицу
сопряженности (рис.2.3), где
.
Пусть даны два таких признака и построены
их гистограммы, не обязательно графически,
а, например, в виде числового ряда.
Совместное распределениеNнаблюдений
одновременно поrзначениям первого
признакаX и поsзначениям
второго признакаYобразуют таблицу
сопряженности (рис.2.3), где
![]() ,
,
![]() - маргинальные частоты, то есть частоты
независимого распределения значений
каждого из данных двух признаков.
- маргинальные частоты, то есть частоты
независимого распределения значений
каждого из данных двух признаков.

Рис. 2.3. Таблица сопряженности двух признаков.
Для такой таблицы
требуется проверить гипотезу Н о
статистической независимости признаков.
Пусть pi j- вероятность
того, что значениеxiпризнакаXсоответствует значениюyj признакаY. Тогда
при справедливости гипотезы Н о
независимости признаков в таблице
соблюдается соотношение![]() для
для![]() постоянных маргинальных вероятностей
постоянных маргинальных вероятностей![]() . Тогда совместное распределение двух
признаков определяется
. Тогда совместное распределение двух
признаков определяется![]() неизвестными параметрами, где из
неизвестными параметрами, где из![]() параметров
параметров![]() параметры
параметры![]() можно выразить через остальные.
можно выразить через остальные.
Вычислим величину
![]() как величину
как величину
![]() .
.
Если справедлива исходная гипотеза Н,
то по условию независимости оценки
маргинальных частот определяются как
 .
Тогда получим
.
Тогда получим
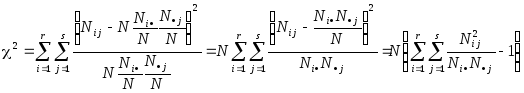 .
.
Так как для таблицы
сопряженности размером
![]() имеетсяrsпеременных значений и
имеетсяrsпеременных значений и![]() параметров, то предельное распределение
параметров, то предельное распределение![]() имеет
имеет![]() степеней свободы. Окончательно:
степеней свободы. Окончательно:
![]() .
.
Для таблицы размером
![]() число степеней свободы
число степеней свободы![]() .
Тогда значение
.
Тогда значение![]() с 1 степенью свободы на уровне значимости
с 1 степенью свободы на уровне значимости![]() определяет вероятность
определяет вероятность![]() ,
где
,
где![]() (найдено по таблице). Следовательно,
значение
(найдено по таблице). Следовательно,
значение![]() встретится только 1 раз из 1000 при
справедливости гипотезы Н о независимости
признаков. Поэтому при справедливости
гипотезы Н крайне маловероятно (
встретится только 1 раз из 1000 при
справедливости гипотезы Н о независимости
признаков. Поэтому при справедливости
гипотезы Н крайне маловероятно (![]() ),
что наблюдаемые и ожидаемые частоты
отличаются настолько, величина оценки
окажется
),
что наблюдаемые и ожидаемые частоты
отличаются настолько, величина оценки
окажется![]() .
Если же это так, то гипотезу Н следует
отвергнуть.
.
Если же это так, то гипотезу Н следует
отвергнуть.
Таким образом, с помощью
теста
![]() можно оценить степень риска (вероятность
ошибки первого рода), предполагая
существование связи между признаками.
Большие значения
можно оценить степень риска (вероятность
ошибки первого рода), предполагая
существование связи между признаками.
Большие значения![]() говорят о значимом отклонении от гипотезы
независимости, то есть о связи.
говорят о значимом отклонении от гипотезы
независимости, то есть о связи.
Но в то же время тест
![]() не дает возможности измерить силу связи.
Поэтому для измерения силы связи логично
использовать некоторую характеристику,
принимающую минимальное значение при
отсутствии связи и максимальное значение
при максимальной связи. Критерий
не дает возможности измерить силу связи.
Поэтому для измерения силы связи логично
использовать некоторую характеристику,
принимающую минимальное значение при
отсутствии связи и максимальное значение
при максимальной связи. Критерий![]() зависит от объема выборкиN. Поэтому
Пирсон использовал в качестве меры
связи между двумя признаками величину
среднеквадратичной сопряженности
зависит от объема выборкиN. Поэтому
Пирсон использовал в качестве меры
связи между двумя признаками величину
среднеквадратичной сопряженности![]() .
При независимости
.
При независимости![]() .
Действительно, из
.
Действительно, из![]() следует
следует
![]() и
и![]() .
.
Тогда
![]() .
.
Найдем максимальное значение
![]() .
Очевидно, что справедливы соотношения
.
Очевидно, что справедливы соотношения
![]() и
и![]() .
.
Тогда выполняются соотношения
![]() ,
,![]() и
и
![]() .
.
Тогда
![]() и окончательно:
и окончательно:
![]() .
.
Недостаток такой
характеристики в том, что при
![]() или
или![]()
![]() .
Поэтому А.А.Чупровым был предложен
коэффициент
.
Поэтому А.А.Чупровым был предложен
коэффициент
![]() ,
где
,
где![]() .
.
В свою очередь, коэффициент Чупрова
![]() только при
только при![]() .
Если
.
Если![]() ,
то даже при полной связи
,
то даже при полной связи![]() .
Поэтому Г.Крамером был предложен
коэффициент
.
Поэтому Г.Крамером был предложен
коэффициент
![]() ,
где
,
где![]() .
.
Коэффициент Крамера изменяется в данных пределах независимо от размера таблицы сопряженности.
