2.5. Приведение корреляционной матрицы к диагональной форме

Преобразование корреляционной матрицы к диагональной форме основано на следующем свойстве вещественной (действительной) симметричной матрицы.

Пусть R- невырожденная корреляционная матрица и имеетnразличных собственных чисел. Пусть- соответствующие собственные векторы, выбранные из пар собственных векторов, соответствующих каждому собственному числу, составляющие ортонормированный базис вn-мерном пространстве. Пусть- матрица, столбцами которой являются собственные векторыa_i. Рассмотрим матрицу

где E- единичная матрица. Следовательно, матрицаAявляется ортогональной.

Напомним, что некоторая матрица Aортогональна, если. По уравнениюполучим, где столбцами матрицы в правой части являются векторы. Учитывая, что векторыa_iортогональны, получим

.

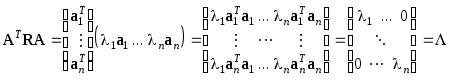Матрица ортогональна, и ее диагональные элементы являются собственными числами. Из условияследуети, так как.

Следовательно, невырожденная корреляционная матрица Rможет быть приведена к диагональной форме путем ортогонального преобразования.

Пусть - некоторый вектор, заданный своими проекциями на осях координат. Рассмотрим вектор, где, а строками матрицыявляются собственные векторыa_i^Tлинейного преобразованияR. Тогда

Следовательно, компонента y_i вектораy - это скалярное произведение собственного вектораa_i и вектораx. С другой стороны, скалярное произведение - это произведение модулей векторовa_i иx на косинус угла между ними. Так как, то это есть произведениена косинус угла междуa_i иx - проекция вектораxнаa_i. Поэтому векторxпредставлен своими проекциямиy_iна ортонормированный базис собственных векторов корреляционной матрицыR. Можно считать, что новый базисобразует новоеn-мерное пространство признаков, принимающих свои значения наNобъектах.

Значения nпризнаковY_i, как бы измеренных наNобъектах, образуют новую матрицу данных, полученную из матрицыXортогональным преобразованиемA:

.

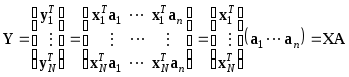Корреляционная матрица R, вычисленная по матрицеX, представляет собой матрицу

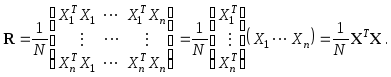
Вычислим среднее признака Y_j

,

так как матрица Xстандартизована. Вычислим величину

Тогда матрица является ковариационной матрицей, вычисленной по матрицеY. Диагональная структура матрицыпоказывает, как и следовало ожидать, независимость признаков. Собственные числа_iявляются дисперсиями этих признаков, то есть. Если разделить значения компонент каждого признакаY_iна величину, то матрицаYбудет приведена к стандартизованному виду. Тогда преобразованиедаст стандартизованную матрицу данныхY с единичной корреляционной матрицей:

2.6. Геометрическая интерпретация главных компонент на плоскости

Пусть в соответствии со статистической гипотезой порождения матрицы данных X вn-мерном пространстве признаков существует многомерное нормальное распределение с плотностью вероятности. Для стандартизованной матрицыXмы полагаем, что

.

Проведем ортогональное преобразование матрицы данных Xв новую матрицу данных, гдеA- матрица, столбцами которой являются собственные векторы корреляционной матрицыR. Тем самым мы перешли в новое признаковое пространство, образованное ортонормированным базисом линейного преобразованияR. Очевидно, что в новом признаковом пространстве задано нормальное распределение с плотностью вероятности

.

Так как то

,

;.

Тогда .

Пусть n = 2, тогда двухмерное нормальное распределение имеет вид

.

Рассмотрим уравнение . Из курса аналитической геометрии известно, что это уравнение линии второго порядка. При заданномpи найденныхданная линия является линией постоянного значения плотности вероятности. Преобразуем данное уравнение линии второго порядка к каноническому виду. Так как, то данное уравнение является каноническим уравнением эллипса в системе координат, образованной собственными векторами, которые соответствуют собственным числам.

Если r>0, тои система главных компонентy₁0y₂повернута на 45⁰относительно исходной системы координатx₁0x₂. Еслиr<0, тои система главных компонентy₁0y₂повернута на 135⁰ относительноx₁0x₂.

Если r=0, то. Тогда уравнение эллипса представляет собой уравнение окружностирадиуса. В этом случае система главных компонентy₁0y₂может быть ориентирована в любом направлении, то есть любое направление является главным для такого линейного преобразованияR. Еслиr=1, то. Тогда уравнение эллипса для линии постоянного значения плотности вероятности вырождается в уравнение для двух точек, расположенных на оси 0y₁, вида(рис. 2.1).

Рис.2.1. Главные компоненты

Определим уравнение максимального эллипса в соответствии с правилом “трех сигм”, согласно которому 99.73% всех наблюдений сосредоточено внутри него.

Согласно свойствам канонического уравнения эллипса его главная ось совпадает с направлением первой главной компоненты 0y₁. Длина главной полуоси составляет величину. В то же время максимальное положительное случайное отклонение величиныy₁на оси 0y₁от центра координат с вероятностью 0.9973 не превышает величины. Следовательно,, откудаp=9.

Проведя те же рассуждения для второй оси максимального эллипса, получим, что уравнение имеет вид и описывает линию постоянного значения плотности вероятности на уровне

.

Так как длина главной полуоси равна , то при увеличении значенияrдлина главной полуоси увеличивется. В то же время длина второй полуоси эллипсауменьшается при увеличенииr. Следовательно, чем сильнее связаны признакиX₁иX₂корреляционной зависимостью, тем больше дисперсияпризнакаY₁и меньше дисперсияпризнакаY₂при неизменной суммарной дисперсии.