31

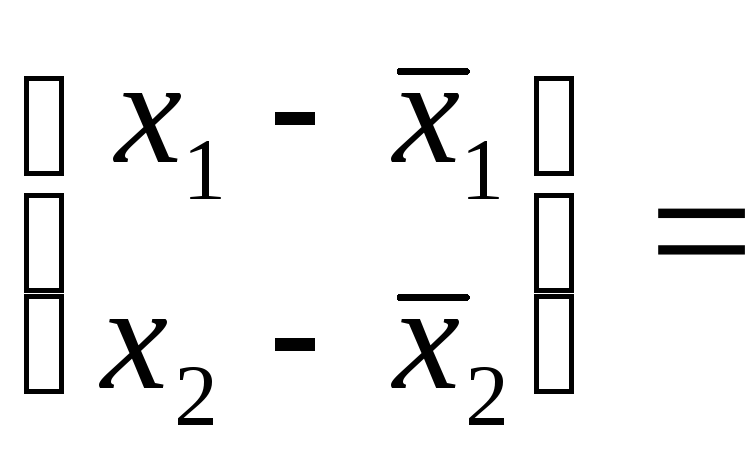
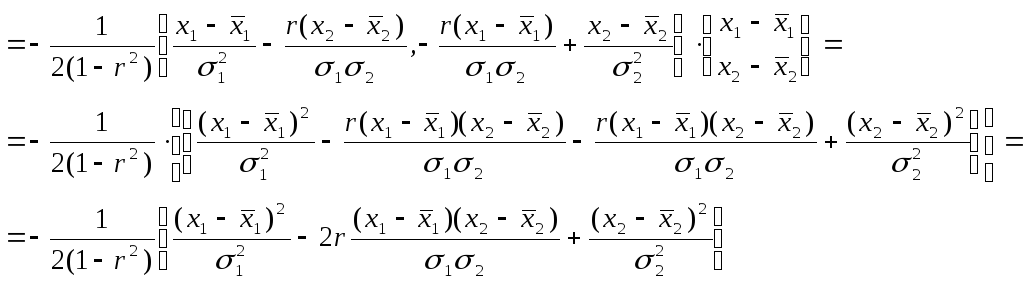
Тогда плотность распределения имеет вид

выражения, в котором коэффициент корреляции, матожидания и дисперсии признаков X₁ и X₂ являются основными числовыми характеристиками распределения. Очевидно, что в случае независимости данных признаков r₁₂=r= 0 и выполнено условие

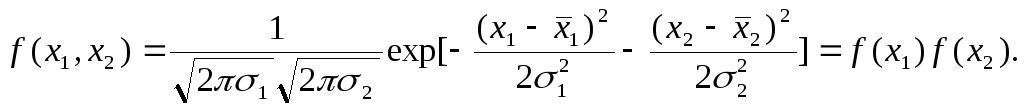
В случае линейной зависимости данных признаков r₁₂ = г = ±1, и распределение f(x₁,x₂) является вырожденным, так как Det = 0.

2.3. Корреляционная матрица и ее

ОСНОВНЫЕ СВОЙСТВА

При анализе связей важное значение имеет структура взаимосвязей между признаками. Как известно, измерителем линейной связи между признаками служит коэффициент корреляции или, в более общем случае, коэффициент ковариации. С другой стороны, вектор средних и матрица ковариаций являются исчерпывающими характеристиками нормального закона распределения. Поэтому остановимся более подробно на свойствах корреляционной матрицы.

32

Корреляционная матрица R(n х n) является симметричной, с единичной главной диагональю, положительно полуопределенной матрицей. Напомним из линейной алгебры, что квадратная матрица, не обязательно симметричная, называется положительно полуопределенной, если для любого вектора Y=(y₁,… y_n)­^T квадратичная форма y­^TRy0 не отрицательна. Квадратная матрица R положительно определена, если для любых у квадратичная форма y­^TRy > 0 строго положительна. В данном свойстве матрицы R легко убедиться:

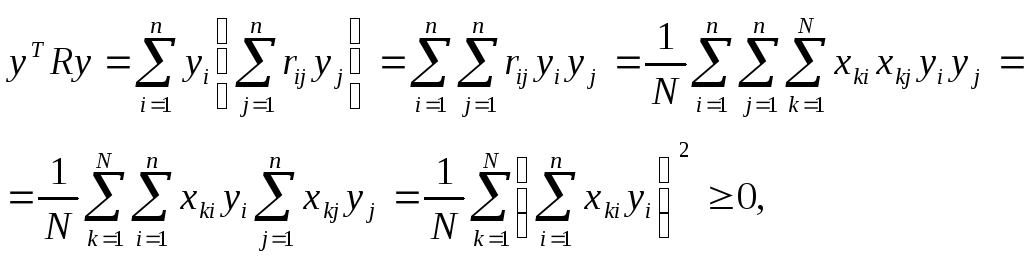
где - коэффициент корреляции, вычисленный как скалярное произведение признаков Xi и X)i в стандартной матрице X.

Заметим, что при ненулевом векторе у квадратичная форма y­^TRy может обратиться в нуль, только если признаки X_i = (x_1i,… x_Ni )^T , i=1,...n линейно зависимы между собой.

Действительно, пусть все признаки X_i , линейно зависимы между собой. Тогда матрица R=(r_ij =1), i = 1,... n, j= 1,... n состоит из единиц, если линейная связь, например, положительна. Тогда для некоторого вектора у получим

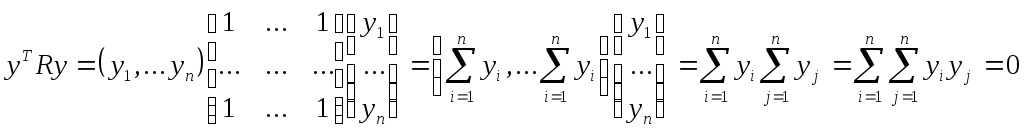
очевидно, что данное число представляет собой сумму всевозможных комбинаций попарных произведений координат вектора у. Все попарные произведения координат данного вектора можно представить в виде квадратной матрицы размером п х п:

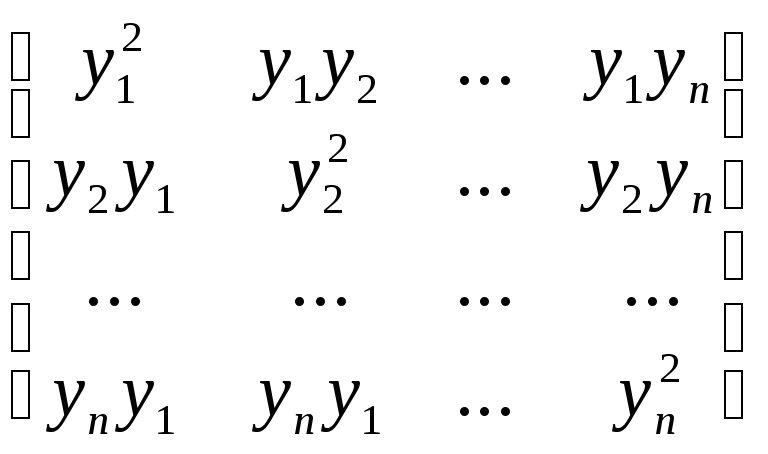=yy^T

Матрица yy^T является симметричной, а сумма ее диагональных элементов представляет собой квадрат длины вектора у и всегда положительна для ненулевого у. Следовательно,

33

равенство y^T Ry = 0 выполняется только, когда сумма диагональных элементов равна по модулю и противоположна по знаку сумме недиагональных элементов

Для случая n = 2 получим: Решив данное квадратное уравнение относительно y₁, получим, что у^TRy = 0 при y₁ = - y₂.

Но признаки X_i представляют собой результаты измерений, где часто число объектов N много больше числа признаков п. Поэтому, в силу возможных ошибок и неточностей измерений, не говоря уже о случайных помехах, линейная зависимость признаков X_i маловероятна. Поэтому, как правило, данная квадратичная форма оказывается строго положительной при любом ненулевом векторе у.

Поэтому корреляционная матрица R на практике считается положительно определенной. В этом случае detR всегда ненулевой, а корреляционная матрица всегда имеет обратную, то есть является невырожденной.

2.4. Собственные векторы и собственные числа корреляционной матрицы

Собственным вектором корреляционной матрицы R, соответствующим собственному числу , называется ненулевой вектор х = (х₁... х_n)^T , удовлетворяющий уравнению Rx =  х.

Как известно из линейной алгебры, матрица R рассматривается в данном случае как матрица линейного преобразования вектора х в вектор х. Это означает, что для данного линейного преобразования R в n-мерном пространстве существует такое направление, что преобразование R только растягивает вектор х в  раз, сохраняя его ориентацию.

Векторное уравнение можно переписать в виде однородного уравнения относительно х: (R - Е)х = 0. Данное уравнение имеет ненулевое (нетривиальное) решение только тогда, когда

определитель det(R-Е) равен нулю. Данный определитель представляет собой уравнение относительно Х и является полиномом n степени вида (-1)ⁿ " + (-1)^n-1 p₁^n-1+…+p_n=0. Данный полином называется характеристическим полиномом (многочленом), а уравнение det(R-Е) = 0 - характеристическим уравнением. Характеристическое уравнение имеет n, вообще говоря, различных корней. При этом его корни _ являются собственными числами преобразования R. В качестве собственных векторов х_i i= 1,... п линейного преобразования R, соответствующих собственным числам _i, i =1,…n, берутся векторы единичной длины каждый из которых удовлетворяет соответствующему характеристическому уравнению det(R-_iE)=0.

Рассмотрим случай п=1. Тогда получим

34

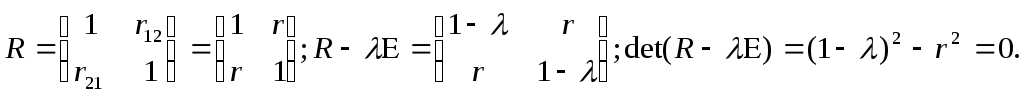
Решением квадратного уравнения ^-2r²=0 относительно  являются корни _r и _=1-r.

Отметим следующие свойства собственных чисел.

1)_>_>0. Так как корреляционная матрица R практически положительно определена, то при произвольном п все ее собственные числа являются действительными и строго положительными _>_>…>_n> 0 .

2) _+_=2. Вычислим след матрицы R как сумму ее диагональных элементов trR =r₁₁+r₂₂=1+1=2. Следовательно, trR=_+_, то есть сумма собственных чисел корреляционной матрицы равна ее следу. При произвольном п получим = trR.

3)__ =1-г² . Определитель корреляционной матрицы равен detR в 1 - г² . Следовательно, det R=__. При произвольном n получим Следовательно, произведение собственных чисел равно определителю корреляционной матрицы, взятому со знаком плюс, так как все собственные числа положительны.

Найдем собственные векторы х₁ и х₂, соответствующие собственным числам _ и _. Из характеристического уравнения следует, что первый вектор найдется из уравнения

Согласно определению = 1. Тогда получим систему уравнений

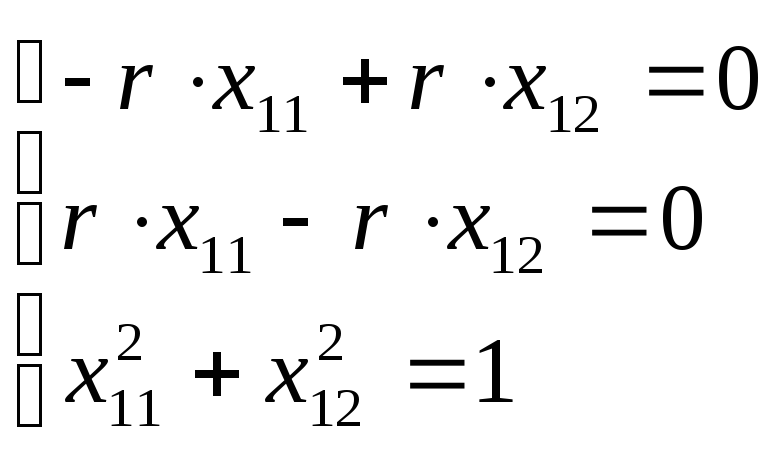
Из решения данной системы следует, что x₁₁ = x₁₂ = ±/2 = ±0.707. Два решения указывают на противоположные направления вдоль диагонали первого и третьего квадрантов плоскости координат:

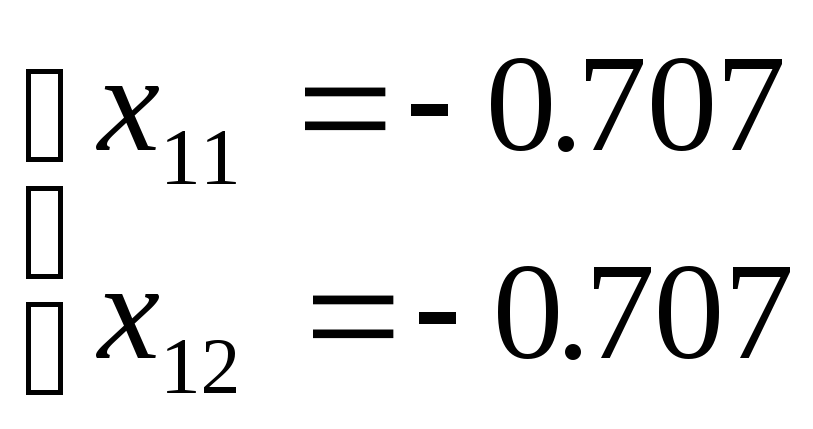
35

Второй вектор найдется из уравнения:

В результате получим два решения, указывающие на противоположные направления вдоль диагонали второго и четвертого квадрантов плоскости координат:

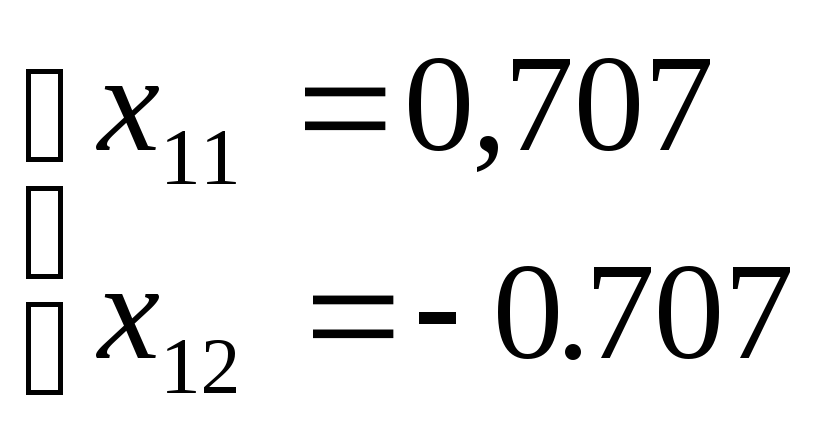
Как сразу нетрудно заметить, собственные векторы матрицы R, то есть вещественной симметричной матрицы, соответствующие различным собственным числам, ортогональны между собой. Покажем это для произвольного п.

Рассмотрим уравнения

Rx₁=_x₁ и Rx₂=_ x₂, где __

Домножим каждое из уравнений на собственный вектор другого уравнения и получим

и

Так как

то, вычтя одно уравнение из другого, получим

Отсюда следует, что = 0. Следовательно, собственные векторы линейного преобразования R образуют ортонормированный базис в n-мерном пространстве. Такие векторы называются главными компонентами корреляционной матрицы.

Главные компоненты корреляционной матрицы обладают весьма важными свойствами, которые имеют содержательный смысл в обработке данных и поэтому широко используются. Ниже мы покажем геометрический смысл главных компонент на плоскости.

36