
- •1.1. Элементарные сведения о перестановках
- •1.2. Определители
- •1.2.1. Определитель n-ого порядка
- •1.2.3. Основные свойства определителей.
- •1.2.4. Умножение определителей.
- •1.2.5. Дифференцирование определителя.
- •1.3.1. Основные определения
- •1.3.2. Операции над матрицами
- •Тема 2. Элементарная теория погрешностей
- •2.1. Абсолютная и относительная погрешности
- •2.2. Основные источники погрешностей
- •2.3. Десятичная запись приближенных чисел. Значащая цифра. Число верных знаков
- •2.4. Округление чисел
- •2.5. Связь относительной погрешности приближенного числа с количеством верных знаков этого числа
- •2.6. Погрешность суммы
- •Очевидно, что
- •2.7. Погрешность разности
- •2.18. Понятие о погрешностях машинной арифметики
2.4. Округление чисел
Часто бывает надобность в округлении этого числа, т.е. в замене его числом а1 с меньшим количеством значащих цифр. Число а1 выбирают так, чтобы погрешность округления а1 - абыла минимальной.
Правило округления (по дополнению). Чтобы округлить число до п значащих цифр, отбрасывают все цифры его, стоящие справа от п-й значащей цифры, или, если это нужно для сохранения разрядов, заменяют их нулями. При этом:
если первая из отброшенных цифр меньше 5, то оставшиеся десятичные знаки сохраняются без изменения;
если первая из отброшенных цифр больше 5, то к последней оставшейся цифре прибавляется единица;
если первая из отброшенных цифр равна 5 и среди остальных отброшенных цифр имеются ненулевые, то последняя оставшаяся цифра увеличивается на единицу;
если же первая из отбрасываемых цифр равна 5 и все остальные отброшенные цифры являются нулями, то последняя оставшаяся цифра сохраняется неизменной, если она четная, и увеличивается на единицу, если она нечетная (правило четной цифры).
При применении правила округления погрешность округления не превосходит ½ единицы десятичного разряда, определяемого последней оставленной значащей цифрой.
2.5. Связь относительной погрешности приближенного числа с количеством верных знаков этого числа
Теорема.
Если положительное приближенное число
а имеет п верных десятичных знаков в
узком смысле, то относительная погрешность
этого числа не превосходит
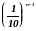 ,
деленную на первую значащую цифру
данного числа, т.е.
,
деленную на первую значащую цифру
данного числа, т.е.
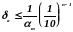 ,
,
где т – первая значащая цифра числа а.
Следствие 1. За предельную относительную погрешность числа а можно принять
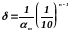 , (2.9)
, (2.9)
где т – первая значащая цифра числа а.
Следствие
2.
Если число а
имеет больше двух верных знаков, т.е.
п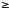 2,
то практически справедлива формула
2,
то практически справедлива формула
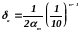 .
.
Приведенная теорема дает возможность по числу верных знаков приближенного числа
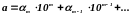 (2.11)
(2.11)
определить его относительную погрешность .
Для решения обратной задачи – определения количества п верных знаков числа (2.11), если известна его относительная погрешность , обычно пользуется приближенной формулой:
= /а (а>0),
где - абсолютная погрешность числа а.
Отсюда
=а. (2.12)
Учитывая
старший десятичный разряд числа
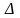 ,
легко установить количество верных
знаков данного приближенного числа а.
В частности, если
,
легко установить количество верных
знаков данного приближенного числа а.
В частности, если
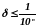
то из формул (2.11) и (2.12) имеем:
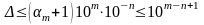
т.
е. число а
заведомо имеет п
верных десятичных знаков в широком
смысле. Аналогично, если
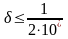 ,
то
число
а
имеет п
верных десятичных знаков в узком смысле.
,
то
число
а
имеет п
верных десятичных знаков в узком смысле.
2.6. Погрешность суммы
Теорема 1.Абсолютная погрешность алгебраической суммы нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел
Пусть х1, х2, …, хп - данные приближенные числа. Рассмотрим их алгебраическую сумму
и= х1х2…хп .
Очевидно, что
= х1х2…хп
и, следовательно,

2. Если слагаемые – одного и того же знака, то предельная относительная погрешность их суммы не превышает наибольшей из предельных относительных погрешностей слагаемых.
