4. Построение графиков с использованием интервальной переменной

Х отя при построении графиков в Mathcad задание аргумента необязательно, иногда оно бывает просто необходимо. Для этого в Mathcad используют интервальную переменную. Например, нам необходимо задать промежуток от -5 до 5 с шагом 0,5. Для этого сначала пишется имя переменной, затем используется знак присваивания значения. Далее указывается начальное значение промежутка, через запятую второе значение. После чего на панели инструментов Matrix (Матрицы), выбирается инструмент интервальной переменной m..n и указывается конечное значение промежутка.

После этого задается формула для графика функции, где в качестве аргумента указывается имя интервальной переменой. Все остальное делается, как уже было описано выше. Например, построим график функции на промежутке от 0 до 2 с шагом 0,01 (см. рис. 7).

5. Построение графиков в полярной системе координат

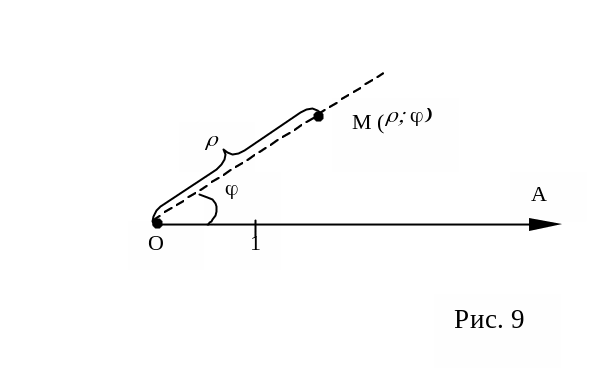
Полярная система координат определяется заданием некоторой точки, называемой полюсом, исходящего из этой точки луча ОА, называемого полярной осью и масштаба для измерения длин. (Рис 8.)

К роме того, при задании полярной системы координат должно быть сказано, какие повороты вокруг точки О считаются положительными. Мы с вами будем считать положительными повороты против часовой стрелки. Полярными координатами произвольной точки М (относительно заданной системы) называются числа

=ОМ; =, причем угол измеряют в радианах. (Рис.9).

Символ М(; ) обозначает, что точка М имеет полярные координаты r и j.

Обратите внимание, что так как r - расстояние от начала координат до точки, то оно не может быть отрицательным.

Полярный угол имеет бесконечно много значений, отличающихся друг от друга на величину 2n. Значение полярного угла удовлетворяющего неравенствам , называется главным.

Построим окружность радиусом 5 с центром в начале координат.

В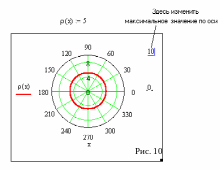 декартовой системе координат уравнение окружности c с центром в начале координат выглядит как: x²+y²=R². полярной же системе это уравнение согласно определению запишется как =const (расстояние от центра постоянная заданная величина). Вы видите насколько проще уравнение окружности в полярной системе координат. Поэтому для построения графика остается записать это уравнение и выбрать мастер построения графика в полярных координатах (см. рис. 10). Чтобы всю окружность стало видно измените максимальное значение оси.

Э то интересно. Естественно между полярными и декартовыми координатами существует определенная взаимосвязь. Для того, чтобы обнаружить эту связь наложим друг на друга полярную и декартовую системы координат так, чтобы их центры совместились, а полярная ось легла на ось абсцисс (Рис.11)

Вспомнив основные тригонометрические соотношения в прямоугольном треугольнике, выразим координаты М(х₀,у₀), через r и j. А затем используя определение тангенса и теорему Пифагора выразим

М(r , j) через х₀ и у_0.

х₀=r cos(j)

у₀=r sin(j)

Задание для самостоятельной работы

1. Построить графики следующих функций с помощью интервальной переменной на указанных промежутках:

А)

В)

2. Построить графики функций в полярной системе координат:

А)

В)

С)

D)

Трехмерные, или 3D-графики, отображают функции двух переменных вида Z(X, Y). При построении трехмерных графиков в ранних версиях MathCAD поверхность нужно было определить математически (Рисунок 2, способ 2). Теперь применяют функцию MathCAD Create­Me­sh.

Create­Me­sh(F (или G, или f1, f2, f3), x0, x1, y0, y1, xgrid, ygrid, fmap)

Создает сетку на поверхности, определенной функцией F. x0, x1, y0, y1 – диапазон изменения переменных, xgrid, ygrid – размеры сетки переменных, fmap – функция отображения. Все параметры, за исключением F, - факультативные. Функция Create­Me­sh по умолчанию создает сетку на поверхности с диапазоном изменения переменных от –5 до 5 и с сеткой 2020 точек.

Пример использования функции Create­Me­sh для построения 3D-графиков приведен на Рисунке 2, способ 1. На Рисунке 2 построена одна и та же поверхность разными способами, с разным форматированием, причем изображены поверхности и под ними те же поверхности в виде контурного графика. Такое построение способно придать рисунку большую наглядность.

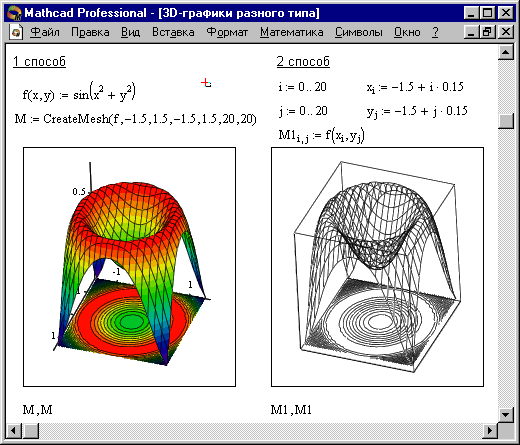
Рисунок 1. Пример построения на одном рисунке двух 3D-графиков разного типа

Нередко поверхности и пространственные кривые представляют в виде точек, кружочков или иных фигур. Такой график создается операцией Вставка  График  3D Точечный, причем поверхность задается параметрически – с помощью трех матриц (X, Y, Z) (см. Рисунок 3, способ 2), а не одной как в примере на Рисунке 2. Для определения исходных данных для такого вида графиков используется функция CreateSpace (см. Рисунок 3, способ 1).

Рисунок 2. Построение 3D Точечных графиков

Create­Space (F , t0, t1, tgrid, fmap)

Возвращает вложенный массив трех векторов, представляющих х-, у-, и z‑координаты пространственной кривой, определенной функцией F. t0 и t1 – диапазон изменения переменной, tgrid – размер сетки переменной, fmap – функция отображения. Все параметры, за исключением F, - факультативные.