Эксперименты в открытом поле
Кажущаяся (или феноменальная) величина оказывается чрезвычайно сложным образованием. Мы уже отмечали, что константность величины, по-видимому, нарушается при большой удаленности объекта в том смысле, что очень далекий человек кажется маленьким, даже если мы оцениваем его рост в 180 см. То же самое имеет место при наблюдении за железнодорожными путями: нам кажется, что рельсы вдали сходятся, хотя мы знаем, что это не так. Следует отметить, однако, что кажущаяся конвергенция линий не так велика, как это должно было бы следовать из проекции угла на сетчатке.
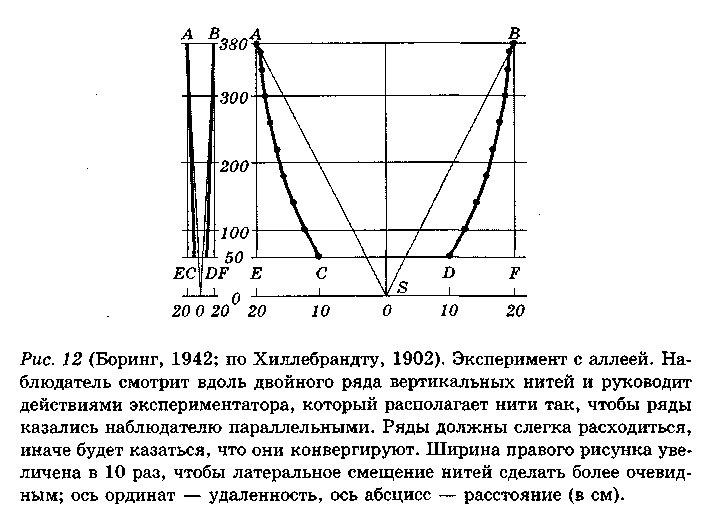
Обычно кажущаяся величина занимает промежуточное положение между величинами, соответствующими закону константности и закону угла зрения. Эта увлекательная тема интенсивно обсуждалась в прошлом веке под общим названием «проблемы аллеи» (Боринг, 1942).
Один из самых корректных экспериментов в этой области был поставлен Хиллебрандтом в 1902 году. Он просил испытуемых так расположить два ряда подвешенных нитей (наподобие двойного ряда деревьев вдоль дороги), чтобы они казались параллельными (рис. 12).
Ясно, что ширина аллеи должна увеличиваться по мере удаления от наблюдателя, но фактически она возрастает значительно медленнее, чем это требуется для сохранения постоянного угла зрения.
Все сказанное касалось кажущейся, или феноменальной величины. Если же вернуться к вопросу об оценке величины, то дело оказывается значительно проще, даже если речь идет о незнакомых объектах на больших расстояниях. Гибсон (1947, 1950) располагал столбики на различных расстояниях от наблюдателя в пределах 800 м. Столбики варьировали по
364
высоте от 38 до 243 см, и наблюдатель не знал их действительных размеров. Его задачей было оценить размеры удаленного (эталонного) столбика путем приравнивания его к одному из ряда ранжированных (сравниваемых) столбиков. Сравниваемые столбики находились за спиной испытуемого, поэтому, чтобы сделать выбор, он должен был повернуться; прямое сопоставление эталонного и сравниваемого столбиков было невозможно. Ответы наблюдателя оказались в очень хорошем соответствии с законом константности, как это видно из результатов, полученных в эксперименте с эталонным столбиком, равным 178 см.
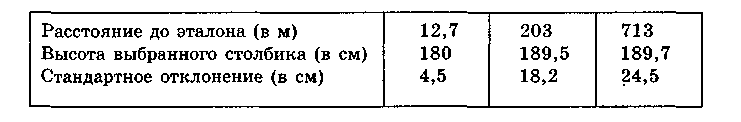
Для четырех промежуточных расстояний результаты оказались сходными. Даже при расстоянии 713 м, когда столбик был едва виден, оцениваемый размер его не уменьшался; напротив, имела место незначительно выраженная противоположная тенденция к сверхконстантности.
365
Эти результаты ясно показывают, что можно весьма точно судить о размере, если имеется адекватная информация об удаленности. И тем не менее работа, которую при этом выполняет нервная система, чрезвычайно сложна. Предположим, эта задача поручена топографу. Прежде всего он определил бы а (размер сетчаточного образа), D (удаленность) и вычислил бы А (размер эталона). Затем он подставил бы новое значение Dc (расстояние, на котором находится сравниваемый столбик), после чего нашел бы ас (размер сетчаточного образа сравниваемого столбика, равного эталонному). Затем он выбрал бы соответствующий столбик из ряда сравниваемых. Этот пример показывает, что любая теория «бессознательной геометрии» наивна, если понимать ее буквально. Наблюдатель, подобно электронно-вычислительной машине, совершает операции, эквивалентные описанным выше, автоматически и мгновенно. Более того, никого не удивляет его способность делать это; она кажется «естественной». Лишь осознав всю сложность перцептивных процессов, можно понять, насколько сложны механизмы, лежащие в основе описанных оценок.