Оценка величины как функция признаков удаленности

Хотя эта проблема исследовалась многими другими авторами, мы предпочитаем начать с описания экспериментов Холуэя и Боринга (1941).

В этих экспериментах наблюдатель помещался в месте пересечения двух длинных коридоров, расходящихся под углом 90°. В одном коридоре на расстоянии 3 м от испытуемого находился «сравниваемый стимул». Он представлял собой световое пятно, размер которого испытуемый мог менять. В другом коридоре на различных расстояниях от наблюдателя (от 3 до 36 м) предъявлялось аналогичное пятно. Это был стандартный стимул, фактические (линейные) размеры которого менялись вместе с расстоянием так, что он всегда имел один и тот же угловой размер, равный 1°. Испытуемому ставилась задача так подобрать размер сравниваемого стимула, чтобы он казался равным стандартному стимулу.

Результаты приведены на рис. 10. Прежде чем перейти к их обсуждению, разберемся в обозначениях на графике. Рассмотрим пунктирную линию, идущую параллельно оси абсцисс. Эта прямая представляет множество значений сравниваемого стимула, которые подобрал бы наблюдатель, если бы он руководствовался угловым размером стандартного стимула (необходимо помнить, что стандартный стимул всегда составлял 1° независимо от удаленности). Теперь рассмотрим пунктирную линию, которая располагается по диагонали графика. Она описывает множество значений, которые мы получили бы в случае «полной константности», т.е. если бы наблюдатель всегда точно подравнивал величину сравниваемого стимула к действи-

360

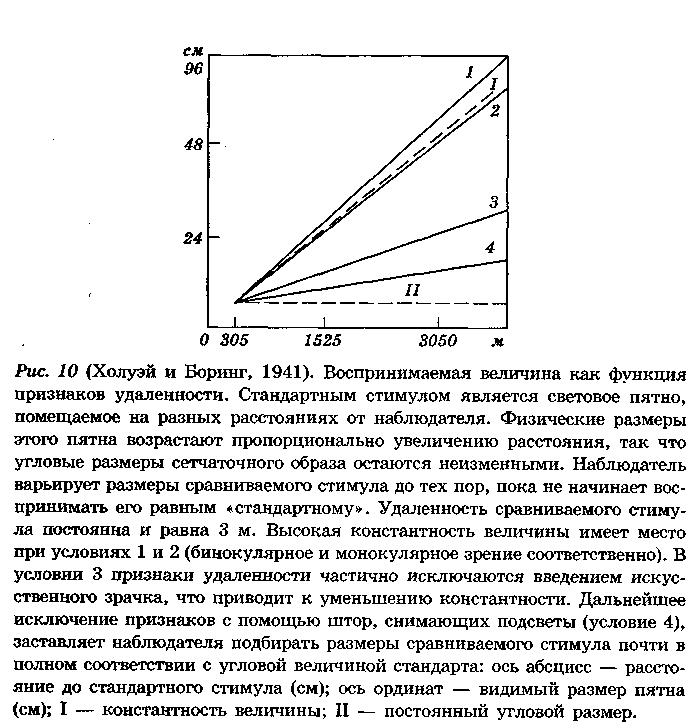
тельной величине стандартного стимула. Тригонометрически можно показать, что на расстоянии 12 метров от наблюдателя 1 градус занимает объект с линейным размером 21 см, а на расстоянии 24 м — объект с линейным размером 42 см и т. д., как это и показано на графике.

Обратимся теперь к результатам. Когда испытуемому были обеспечены условия нормального бинокулярного зрения, он давал результаты, представленные прямой 1. Наблюдался даже незначительный эффект сверхконстантности, что, возможно, было связано со сверхкомпенсацией или некоторой переоценкой удаленности — ведь наблюдатель смотрел вдоль длинного коридора. Прямая 2 показывает результаты, полученные в условиях монокулярного зрения. Восприятие удаленности все еще хорошее: об этом говорит тот факт, что полученные значения

361

находятся в соответствии с законом константности. Но как только был введен искусственный зрачок, устранивший дополнительные признаки удаленности, оценки наблюдателя оказались в промежуточном положении между оценками, соответствующими закону константности и закону угла зрения (линия 3). При этом еще сохранились остатки признаков глубины в виде слабых подсветов от дверей, расположенных вдоль коридора. Когда же и они были исключены с помощью черных штор, результаты еще больше приблизились к закону угла зрения (прямая 4). Позднее Личтон и Лурье (1950) еще более ограничили признаки удаленности, используя экраны, которые не позволяли наблюдателю видеть ничего, кроме светового пятна. В этих условиях не оставалось даже и намека на константность величины. Эти два эксперимента ясно показывают, что наблюдатель может правильно оценивать размеры неизвестного ему предмета лишь в той мере, в какой у него есть надежные источники информации об его удаленности.