
- •Глава I. Числовые множества. 1
- •§1. Множества : символика, операции; числовые множества nìzìqìr
- •§2 Множество комплексных чисел(к.Ч.) : определения, аксиомы, комплексная плоскость; rìc.
- •§3. Алгебраическая форма к.Ч.; арифметические операции с к.Ч.
- •§4. Тригонометрическая и показательная формы к. Ч. ; аргумент к. Числа.
§4. Тригонометрическая и показательная формы к. Ч. ; аргумент к. Числа.
Известно, что между точкой комплексной плоскости и соответствующим к. числом существует взаимно-однозначное соответствие M(x,y)z=(x,y)C.
В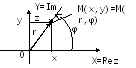 ведем
на комплексной плоскости одновременно
две системы координат –прямоугольную
(оси абсцисс X=Rez
и ординат Y=Jmz)
и полярную
(полюс О и
полярная ось ОХ).
ведем
на комплексной плоскости одновременно
две системы координат –прямоугольную
(оси абсцисс X=Rez
и ординат Y=Jmz)
и полярную
(полюс О и
полярная ось ОХ).
Точка на плоскости определяется
либо ее прямоугольными координатами - абсциссой и ординатой- M(x,y),
л ибо
ееполярными
координатами
– длиной радиус-вектора точки
ибо
ееполярными
координатами
– длиной радиус-вектора точки
![]() и полярным
углом φ
-M(r,φ),
причем
и полярным
углом φ
-M(r,φ),
причем
Так как полярный угол точки определен не однозначно 0+2к; kZ; |0|<2, для взаимно-однозначного соответствия точки и ее полярных координат в качестве полярного угла будем принимать 0: |0|<2.
В дополнение к
обозначениям x=Rez;
y=Imz;
![]() ,введем
для комплексного
числа Z=C
еще два
,введем
для комплексного
числа Z=C
еще два
определения:
Argz==0+2к;kZ– аргумент к.ч.;
argz=0; |argz|<2 -главное значение аргумента к.ч.
Между Rez, Imz, |z| и argz=0 существуют следующие соотношения:
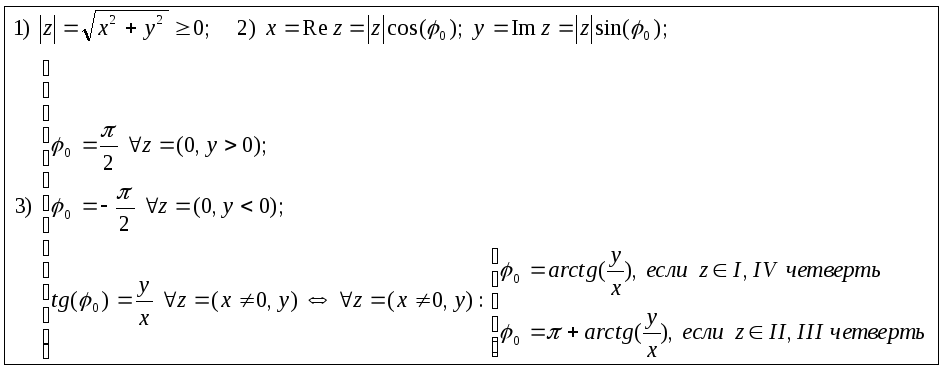
"»Воспоминания»: tg(-0)=- tg(0)
|
0,рад |
/2 |
/3 |
/4 |
/6 |
0 |
|
tg(0) |
+ |
3 |
1 |
1/3 |
0 |
Например,z=1+j0= arg(1+j)=π/4; =Arg(1+j)= π/4+2kπ; kZ.
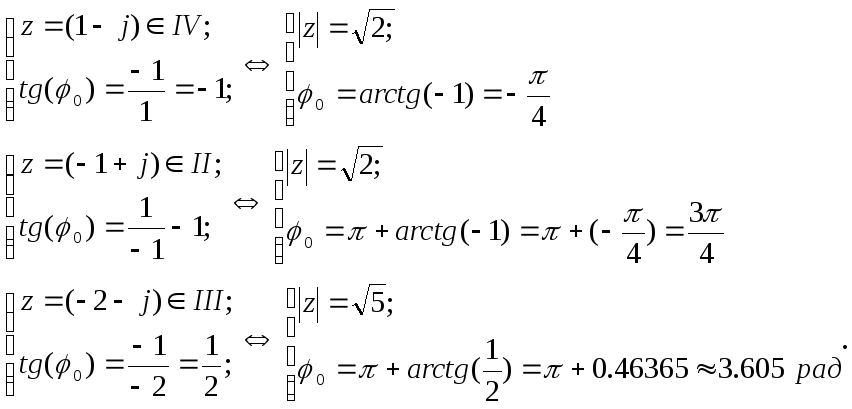
Д/З: найти значения argz для множеств положительных и отрицательных вещественных чисел.
Из алгебраической формы к.ч и соотношений 2) следует тригонометрическая форма к. числа: zC/{0}: z=(x,y)=|z|(cos(0)+jsin(0))
Кроме того, в третьем семестре будет доказана формула Эйлера
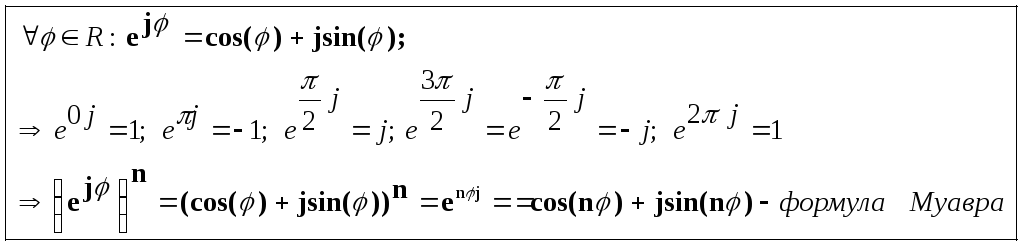
Из формулы Эйлера
и тригонометрической формы следует
показательная
форма к. числа:
![]() Например,
Например,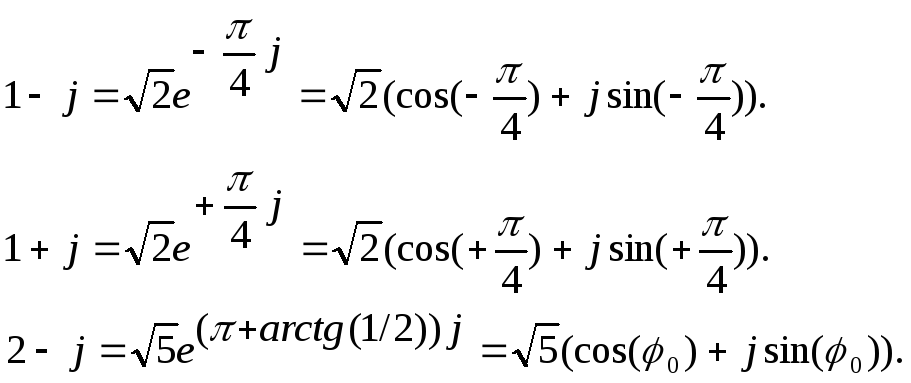
----------------------------------------------------------------------------
Замечания.
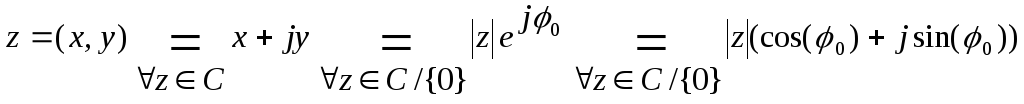
1)Условия равенства к. чисел :
(а)в
алгебраической форме -
![]()
(б)в
показательной и тригонометрической
формах
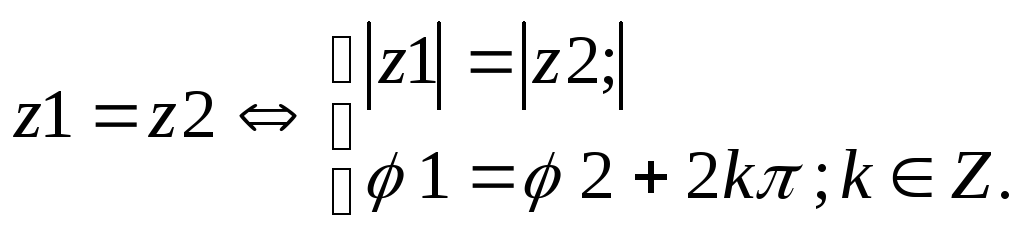
2) Алгебраичесая форма предпочтительна при сложении и вычитании к. чисел;
показательная и тригонометрическая формы «удобны» в операциях умножения, деления и возведения к.чисел в натуральную степень, при этом:
(а)
модули, соответственно, перемножаются,
делятся или возводятся в степень -
![]() ;
;
(б)
аргументы, соответственно, складываются,
вычитаются
или умножаются на показатель степени
-
![]()
3) Так как е2kj=1, в записи конечного результата операций в показательной (тригонометрической) форме используется главное значение аргумента 0; |0|<2: z=|z|exp[0+2k)j]=|z|exp(0j)=|z|(cos(0)+jsin(0)).
Экз. задача. “Найти Rez, Imz, |z|, argz и записать три формы к. числа.
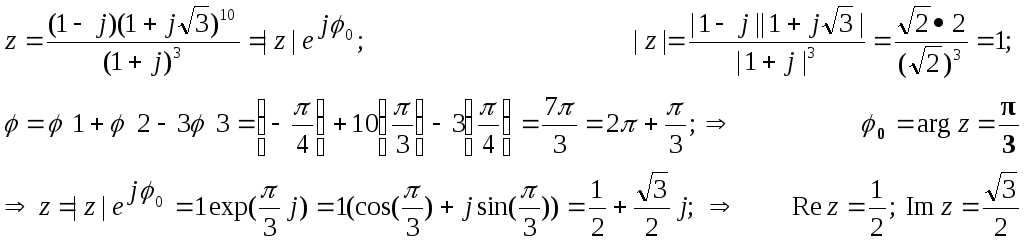
§5.Решение двучленных zn=a и квадратных z2+bz+c=0 уравнений в С; основная теорема алгебры.
Пусть
задано в показательной форме к. число
a=|a|ejφa.
Решение
уравнения zn=a;
![]() будем
искать так же в в показательной форме:
будем
искать так же в в показательной форме:
![]()
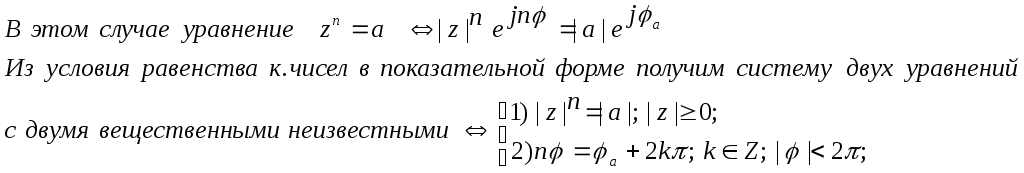
Первое
уравнение имеет единственное решение
-арифметическое значение корня степени
«n»
из неотрицательного числа: 1)
!
![]()
Второе
же уравнение системы имеет множество
решений:
![]()
Однако,
с учетом того, что e2kj=1,
различным комплексным числам
![]() соответствуют лишь “n”
значений аргумента:
соответствуют лишь “n”
значений аргумента:
![]() так
как, например,
так
как, например,![]()
Таким образом,
![]()
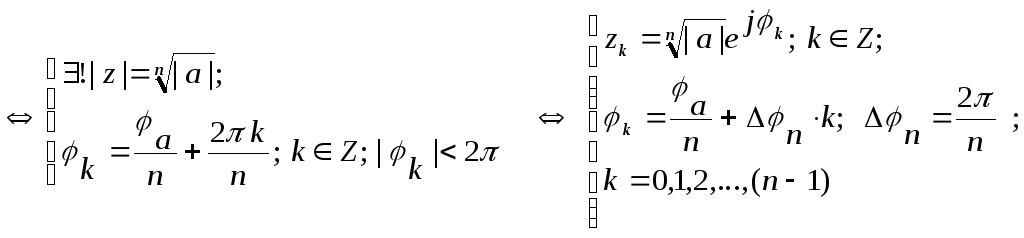
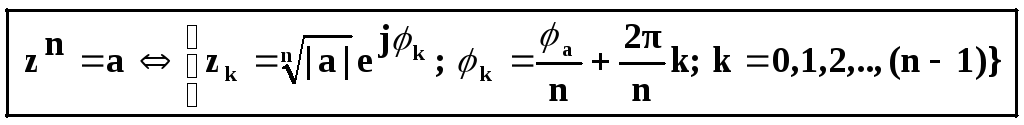 .
.
С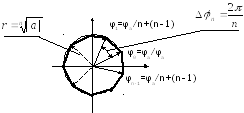 ледовательно,
во множестве к. чисел двучленное уранениеzn=a;
ледовательно,
во множестве к. чисел двучленное уранениеzn=a;
![]() имеет
ровно «n»
различных решений.
Эти решения
имеют одинаковые модули, а их аргументы
отличаются на величину, кратную величине
имеет
ровно «n»
различных решений.
Эти решения
имеют одинаковые модули, а их аргументы
отличаются на величину, кратную величине
![]() .
На комплексной плоскости решения
уравнениярасполагаются
в вершинах правильного n-угольника,
вписанного в окружность радиуса r=
.
На комплексной плоскости решения
уравнениярасполагаются
в вершинах правильного n-угольника,
вписанного в окружность радиуса r=![]() .
.
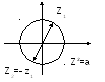
Например,
![]() -
решения двучленного квадратного
уравнения -противоположные
к. числа,
-
решения двучленного квадратного
уравнения -противоположные
к. числа,
![]()
Основная теорема алгебры. «Полином степени «n”
![]()
имеет
ровно «n”
корней
![]() ,
считая совпадающие («кратные») корни,
и единственным образом представляется
в виде произведения
,
считая совпадающие («кратные») корни,
и единственным образом представляется
в виде произведения
![]() ».
».
Например,
1)
![]()
2) z2+1=(z-j)(z+j).
Рассмотрим квадратное
уравнение az2+bz+c=0;
a#0.
Выделим по первым двум слагаемым «полный
квадрат»
![]() и
приведем уравнение к двучленному
квадратному.
и
приведем уравнение к двучленному
квадратному.
![]()
Обозначим
к. число
![]() и запишем
решения
уравнения
(*) в
виде
и запишем
решения
уравнения
(*) в
виде
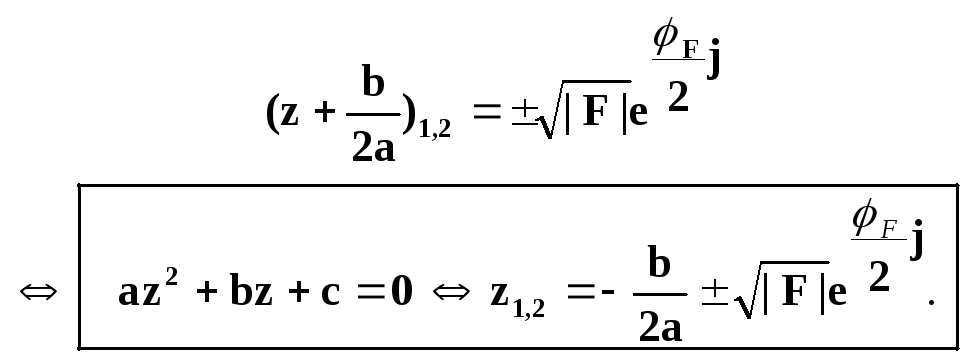
Замечание.
Для квадратного
уравнения с
вещественными коэффициентами
![]() имеют место следующие формулы:
имеют место следующие формулы:
1)
Если D>0
( φF=0),
получим известную формулу корней
квадратного уравнения с положительным
дискриминантом
![]()
Если D<0
(φF=π),
![]() -
комплексно-сопряженные числа !!!;
-
комплексно-сопряженные числа !!!;
например,
![]()
--------------------------------------------------------------------
Экз. задача. 1) Найти и изобразить на к. плоскости все корни уравнения z3+1=0.
(z1=-1;
z2,3=0.5(1![]() ).
2) Решить уравнение z2+2z+5=0
и доказать, что полученные числа - корни
уравнения.
).
2) Решить уравнение z2+2z+5=0
и доказать, что полученные числа - корни
уравнения.
![]()
Экз.+1. «Решив биквадратное уравнение z4+z2+1=0, (а)записать три формы всех его решений; (б)изобразить решения на ; (в) записать разложение на множители полинома P4(z)= z4+z2+1. (z{(1j3)/2}={exp(j/3)}={[cos(/3)+jsin(/3)]}
