10. Уравновешивание масс в механизмах и машинах

10.1. Действие сил на фундамент. Условия уравновешивания

В общем случае в кинематических парах механизмов и машин возникают динамические усилия, переменные по величине и направлению. Через стойку они передаются на фундамент, вызывая дополнительные напряжения в отдельных звеньях, вибрацию и ухудшение условий работы. Чтобы этого избежать, необходимо рационально подобрать и расположить массы звеньев с условием полного или частичного гашения динамических усилий. Эта задача решается при уравновешивании.

Основными динамическими составляющими при работе любого механизма являются силы инерции, которые, как правило, переменны по величине и направлению. Это характерно и для случаев, когда входное звено вращается с постоянной угловой скоростью (рис. 96). Все силы и моменты сил инерции можно привести к главному вектору и моменту относительно выбранной точки:

;

Полностью уравновешенным считается механизм, в котором и , т.е. сила давления стойки на фундамент остаётся постоянной при движении звеньев.

Из теоретической механики известно, что: ,

где масса всех подвижных звеньев; ускорение центра масс системы.

Следовательно, для выполнения условия необходимо, чтобы .

Это равносильно требованию постоянства положения центра масс механизма относительно стойки. Такое уравновешивание называется статическим или уравновешиванием первого рода. В этом случае используется метод заменяющих (сосредоточенных) масс, обладающих массой, центром масс и моментом инерции заменяемого твёрдого тела (звена) с распределённой массой. Если поместить начало системы координат в центр масс системы, то условия эквивалентности заменяемой и заменяющих масс запишутся так:

; ; ; ,

т.е. в общем случае плоского звена необходимы четыре заменяющих массы. В частных случаях число заменяющих масс может быть сведено к двум. Например, для звена АВ (рис. 97) можно ограничиться частичной заменой его массы m дву-

м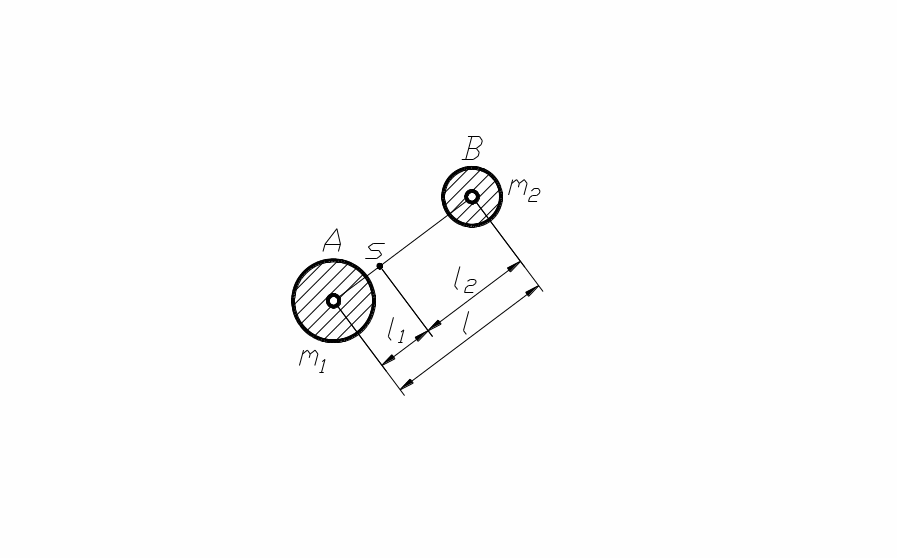 я массами m₁ и m₂, учитывая условия:

; .

Отсюда: ; .

Для полного уравновешивания механизма необходимо выполнение обоих условий: ; , причём выполнение условия решается при

рис. 97 моментном (динамическом) уравновешивании, которое называется уравновешиванием второго рода.

10.2. Уравновешивание с помощью противовесов на звеньях механизма

Рассмотрим последовательность статического уравновешивания на примере четырёхшарнирного механизма (рис. 98, а). Заменяем массы звеньев 1, 2, 3 сосредоточенными массами в точках A, B, C, D, причём в силу неподвижности точек A и D, массы, сосредоточенные в этих точках, можно не учитывать.

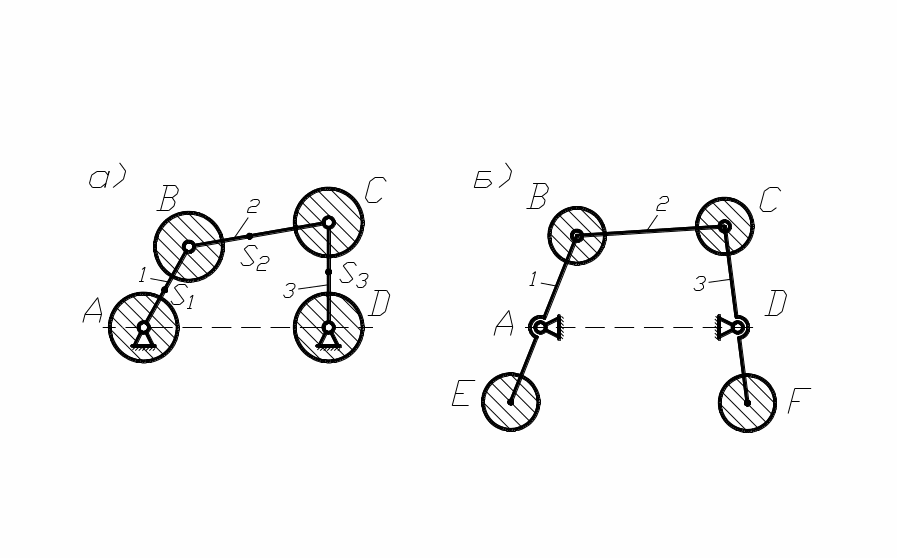
рис. 98

Приведённые массы в точках В и С равны:

;

.

Так как заменяющие массы m_B и m_C совершают вращательное движение, то для уравновешивания сил инерции необходимы противовесы с массами m_Е и m_F, определяемыми из условий (рис. 98, б):

; ,

где, задавая длины противовесов, можно получить их массы и наоборот.

Рассмотрим моментное уравновешивание на примере четырёхшарнирного механизма. Его приближённое моментное уравновешивание можно осуществить после статического уравновешивания, введя в схему механизма два одинаковых дополнительных противовеса (рис. 99), соединённых с зубчатыми колёсами “a” и “b”. Колесо “a” жёстко связано с кривошипом 1 и вращается с угловой скоростью , а равное ему колесо “b”

рис. 99 вращается с той же угловой скоростью , но угловые координаты противовесов отличаются на 180⁰, поэтому момент пары сил инерции от противовесов равен . Подбирая положение точки E, можно обеспечить направление , противоположное направлению , а массу противовесов определяют из условия = .