технология бурения 2

vk.com/club152685050 | vk.com/id446425943

ηГМ = 0,5…0,7. Меньше значения ηГМ соответствуют двигателям с заходностью статоров z1= 9…10, а большие значения – двигателям с заходностью статора z1= 3 …5.

Список используемой и рекомендуемой литературы

2.Симонянц С. Л. Практическое обучение бакалавров по профилю «Бурение нефтяных и газовых скважин»: учебное пособие. – М.: Изд. центр РГУ нефти и газа им. И. М. Губкина, 2011. – 96 с.

3.Симонянц С. Л. Технология бурения скважин гидравлическими забойными двигателями: учебное пособие. – Н.Новгород: Вектор ТиС, 2007. – 160 с.

4.Северинчик Н. А. Машины и оборудование для бурения скважин. – М.:

Недра, 1986. – С. 119.

5.Балденко Д. Ф. Одновинтовые гидравлические машины: в 2 т. / Д. Ф. Балденко, Ф. Д. Балденко, А. Н. Гноевых. – М.: ООО «ИРЦ Газпром», 2007. – Т 2. Винтовые забойные двигатели. – С. 470.

6.Овчинников В. П. Винтовые забойные двигатели для бурения скважин:

Монография / В. П. Овчинников, М. В. Двойников, Д. Р. Аминов, А. И. Шиверских. – Тюмень: ООО «Печатник», 2009. – 204 с.

7.Коротких Н. И. Разработка новых эластомеров для статоров винтовых забойных двигателей и винтовых насосов / Н. И. Коротких, Е. И. Гаврилова // Строительство нефтяных и газовых скважин на суше и на море. – 2003. –

№ 9 – С. 43–44.

8.Балденко Д. Ф. Винтовые забойные двигатели: справочное пособие / Д. Ф. Балденко, Ф. Д. Балденко, А. Н. Гноевых. – М.: Изд. «Недра», 1999. – С. 5–9.

9.ГОСТ26673-85 Государственный стандарт на производство гидравлических забойных двигателей.

10.ТУ39-1118-86 Технические условия на изготовление гидравлических забойных двигателей.

11.ТУ 3664-044-0014707402002, ТУ 3664-005-14030039-2005 Технические условия на двигатели винтовые забойные для бурения и капитального ремонта скважин.

12.Downhole Measurements While Drilling (материалы к семинару фирмы ANADRILL SCHLUMBERGER в Москве, март 1987 г.).

13.Measurement While Drilling (MWD). Gearhart Geodata Services, Aberdeen (проспект).

14.Dyna-Drill. Handbook. The 2-nd edition. USA, 1975.

15.Studie zur Entwicklung eines vorortantriebes nach dem system «Dyna-Drill». Freiberg Bergakademie, 1969.

16.Кулябин Г. А. Технология углубления скважин на нефть и газ. –Тюмень:

Изд-во «Вектор Бук», 2001. – С. 106–123.

79

vk.com/club152685050 | vk.com/id446425943

17.ОСТ 39-164-84 Передача зубчатая ротор-статор винтового забойного двигателя. Исходный контур. Расчет геометрии.

18.Крылов В. И. Гидродинамические особенности бурения горизонтальных скважин / В. И. Крылов, В. В. Крецул // Нефтяное хозяйство. –2000. – № 6.

19.Методика по выбору реологических свойств буровых растворов и техно-

логии очистки горизонтальных скважин. ВРД 39-1.8-045-2001 / А. Г. Потапов, С. В. Васильченко, А. В. Сутырин. – М.: ОАО «Газпром» ВНИИГАЗ, 2001.

20.Буркунов В. С. Гидравлический расчет промывки скважины при бурении с помощью винтовых забойных двигателей / В. С. Буркунов, Е. Г. Леонов // Геология, бурение, разработка и эксплуатация газовых и газоконденсатных месторождений на суше и на море. – 1998. – С. 23–25.

21.Попов А. Н. Технология бурения нефтяных и газовых скважин: учеб. для вузов / А. Н. Попов, А. И. Спивак, Т. О. Акбулатов и др. – М.: ООО «Не- дра-Бизнесцентр», 2003. – С. 509.

vk.com/club152685050 | vk.com/id446425943

ГЛАВА 9

ГИДРАВЛИЧЕСКАЯ ПРОГРАММА БУРЕНИЯ СКВАЖИН

Авторы-составители:

Акбулатов Т. О., Аксенова Н. А., Грошева Т. В.

Гидравлической программой бурения скважин называется совокупность режимов промывки и других операций, связанных с гидравлическими явлениями и обеспечивающих бурение скважин без осложнений, с максимально высоким качеством при заданных ограничениях по стоимости строительства скважин и выбору бурового оборудования.

Гидравлическая программа включает обоснование параметров и расхода промывочной жидкости, выбор режимов промывки забоя, расчет давлений, определение типа и числа насосов, режимов их работ. Некоторые исследователи включают в гидравлическую программу также определение максимально допустимых скоростей спуско-подъёмных операций (СПО).

Гидравлику обычно относят к прикладным наукам, в которой изучают законы покоя и движения жидких тел и рассматривают способы приложения этих законов к решению конкретных технических задач.

Помимо гидравлики изучением покоя и движения жидкостей занимается другая наука – теоретическая гидромеханика, являющаяся самостоятельным разделом теоретической механики. Гидромеханика характеризует точность и общность решений. Она носит строго математический характер и при исследовании гидравлических явлений исходит из дифференциальных уравнений, описывающих эти явления.

Вотличие от гидромеханики гидравлика строит свои выводы на основе рассмотрения упрощенных схем гидравлических явлений, вводя в то же время в теоретические уравнения эмпирические коэффициенты, получаемые в результате обработки данных опыта, имеющего в гидравлике весьма большое значение.

Основными понятиями, оперируемыми в гидравлике, являются жидкие тела или жидкости, называемые физическими телами, которые легко изменяют свою форму под действием сил самой незначительной величины.

Различают два вида жидкостей: жидкости капельные и газообразные. Все капельные жидкости оказывают большое сопротивление изменению объема и трудно поддаются сжатию, кроме того, для обычных задач гидравлики считается, что растягивающие усилия в жидкости отсутствуют.

Вгидравлике часто вводится понятие идеальной жидкости, которая обладает абсолютной несжимаемостью, полным отсутствием температурного расширения и не оказывает сопротивления растягивающим и сдвигающим усилиям. Наличие у реальных жидкостей сил сопротивления сдвигу определяется особым свойством жидкости – вязкостью.

1

81

vk.com/club152685050 | vk.com/id446425943

О гидравлике буровых растворов было много написано за последние 30–40 лет. Имеется несколько различных концепций, моделей и систем уравнений, которые могут быть использованы для планирования, оптимизации и расчетов гидравлики бурения. Почти во всех случаях разница, возникающая при использовании той или иной концепции, значительно меньше погрешностей самих данных, используемых в расчетах. Вычисление различных гидравлических параметров при бурении очень важно для контроля многих переменных, относящихся к буровым растворам, что позволяет обеспечить безопасное заканчивание скважины с минимумом повреждения пласта при минимальных затратах. Оптимизация любого отдельного гидравлического параметра в первую очередь будет зависеть от места бурения.

9.1. Режим течения промывочных жидкостей

Промывочные жидкости должны обеспечивать очистку забоя от выбуренной породы и транспорт последней на дневную поверхность, высокую эффективность разрушения горной породы на забое, создавать необходимое противодавление на проходимые породы с целью избежать нежелательного поступления пластовых флюидов и разрушения стенок скважины в процессе строительства. Одновременно циркулирующая жидкость охлаждает и смазывает долото и колонну труб.

При бурении гидравлическими забойными двигателями (турбобуры, объемные винтовые двигатели) промывочная жидкость является средством доставки энергии к забойному двигателю. При использовании телесистем промывочная жидкость может служить каналом связи забойных датчиков с поверхностью.

Промывочные жидкости должны создавать на стенках скважины тонкую малопроницаемую фильтрационную корку, затрудняющую поступление фильтратов буровых растворов в продуктивные пласты и в то же время не вносить существенные погрешности при производстве геофизических исследований в скважинах.

Степень выполнения буровыми растворами вышеперечисленных функций определяется их свойствами. Более детально о свойствах буровых растворов, о методах их определения изложено в главе 13.

В элементах циркуляционной системы скважины жидкость по существу движется как единое, невозмущенное цельное тело или цилиндр. Движение происходит таким образом, что тонкий слой жидкости «скользит» вдоль поверхности вмещающего сосуда.

Существует несколько режимов течения жидкостей:

–тип течения, когда все жидкие компоненты потока перемещаются в одном направлении, называется ламинарным потоком;

2

82

vk.com/club152685050 | vk.com/id446425943

–быстрое хаотичное перемещение жидкости во всех направлениях называется турбулентным;

–при некоторых условиях течение может меняться и попеременно переходить из ламинарного в турбулентное и обратно; такое течение называется переходным;

–течение жидкости при сверхнизких скоростях потока — пробковый

(поршневой) режим потока.

Пробковый режим течения. При пробковом потоке жидкость течет в основном как единое, не изменяющееся твердое тело. Движение жидкости происходит ввиду скольжения очень тонкого слоя жидкости вдоль стенки трубы или поверхности направляющей колонны. Пробковый поток обычно имеет место при экстремально низких скоростях потока.

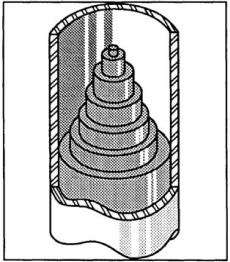
Ламинарный режим течения. Ламинарный поток ньютоновской жидкости в кольцевой трубе показан на рисунке 9.1, его можно представить в виде соосных цилиндрических слоев, перемещающихся относительно друг друга, как в подзорной трубе. Скорость слоя у стенки трубы — нулевая, а скорость слоя в центре трубы — максимальная.

Рис. 9.1. Трехмерное изображение ламинарного потока в трубке с ньютоновской жидкостью

Двухмерный профиль скоростей показан на рисунке 9.2. Степень сдвига, определенная выше как разница скоростей двух слоев жидкости, деленная на разницу двух слоев, представляет собой просто наклон линии в любой точке вдоль профиля скоростей. Скорость сдвига максимальная у стенки и нулевая – в центре трубы. Поскольку у ньютоновских жидкостей напряжение сдвига и скорость сдвига прямо пропорциональны, то напряжение сдвига также максимально у стенки и нулевое – в центре трубы. Ламинарный поток неньютоновской жидкости очень похож на ламинарный поток ньютоновской жидкости с тем исключением, что здесь какая-то часть цилиндрических тел оси в центре трубы может не скользить относительно друг друга. Двухкоординатная эпюра скоростей неньютоновской

3

83

vk.com/club152685050 | vk.com/id446425943

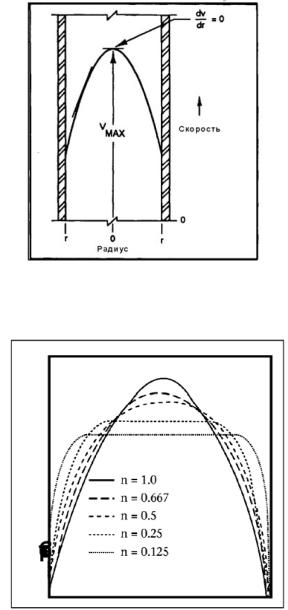
жидкости при ламинарном течении зависит от соотношения напряжения сдвига и степени сдвига. Несколько примеров эпюр скоростей приведены на рисунке 9.3.

Рис. 9.2. Двухмерный профиль скоростей ламинарного потока в трубке с ньютоновской жидкостью

Рис. 9.3. Двухмерный профиль скоростей неньютоновской жидкости при ламинарном течении

Турбулентный режим течения. Турбулентный поток возникает тогда, когда жидкость подвергается беспорядочному, хаотическому, сдвиговому воздействию, возникающему в результате локальных отклонений скорости и направления потока, при этом сохраняется средняя скорость в направлении потока. Лишь у самой стенки существует тонкий слой с регулярным сдвигом. Таким образом, профиль скорости очень крутой у стенок, но практически плоский в любых других местах, что видно на рисунке 9.4.

4

84

vk.com/club152685050 | vk.com/id446425943

Рис. 9.4. Двухмерный профиль скорости турбулентного потока в трубе с ньютоновской жидкостью

Переходный поток. Переходным считается поток, когда течение жидкости не является ни ламинарным, ни турбулентным. Другими словами, отсутствует резкий переход от одного режима течения к другому.

9.1.1. Реологические модели жидкостей. Реометрия

Реологической моделью жидкости называется зависимость касательных напряжений от градиента скорости сдвига в направлении, нормальном вектору скорости, при ламинарном течении:

Графическое изображение такой зависимости называется реограммой. В реологическом смысле все жидкости делятся на ньютоновские и неньютоновские. Ньютоновские жидкости имеют прямо пропорциональную зависимость касательных напряжений от градиента скорости сдвига, описываемую уравнением Ньютона

Реограмма такой жидкости показана на рисунке 9.5.

Для ньютоновских жидкостей отношение касательных напряжений к градиенту скорости сдвига, называемое динамической вязкостью, не зави-

85

vk.com/club152685050 | vk.com/id446425943

Для неньютоновских жидкостей отношение касательных напряжений к градиенту скорости сдвига есть величина переменная (зависит от вели-

чины градиента): τ/(dU/dr) = νar.

Рис. 9.5. Реограмма реологически стационарных жидкостей: 1 – вязкая ньютоновская; 2 – псевдоплатичная, 3 – дилатантная

Неньютоновских жидкостей очень много – это вязкопластичные жидкости (ВПЖ), псевдопластичные (ППЖ), вязкоупругие (ВУЖ), дилантантные жидкости и многие другие.

Для ВПЖ и ППЖ с увеличением градиента скорости сдвига отноше-

ние τ/(dU/dn) уменьшается, жидкости становятся как бы более подвижными.

Дилантантные жидкости с увеличением градиента скорости сдвига за-

густевают, отношение τ/(dU/dn) увеличивается. Дилантантными свойствами обладают водные растворы гипса.

ВУЖ относятся к нестационарным жидкостям. У них касательные напряжения зависят не только от градиента скорости, сдвига, но и от скорости изменения градиента. Примерами ВУЖ является резиновый клей, водные растворы ПАА и других полимеров с разветвленной молекулой.

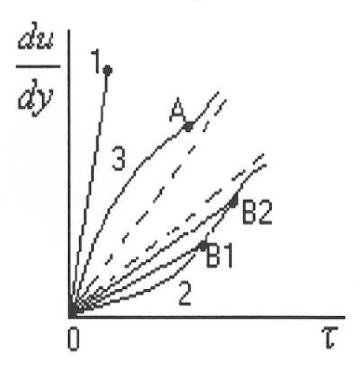
Большинство буровых растворов (глинистых, цементных, глинистополимерных) относятся к классу вязкопластичных жидкостей (ВПЖ), имеющих реограмму, показанную на рисунке 9.6.

6

86

vk.com/club152685050 | vk.com/id446425943

dU/dn

D

C

B

A

Рис. 9.6. Реограмма реальной ВПЖ

Поведение данных растворов может быть описано разными моделями. Реологическая модель Бингама. Была предложена американским уче-

ным Бингамом, изучавшим течение красок

(9.3)

Чаще уравнение Бингама записывают в виде

Из сравнения рисунка 9.6 и 9.7 можно видеть, что уравнение Бингама хорошо описывает близкий к прямолинейному участок ВС реальной реограммы, не описывая криволинейные участки АВ и СD.

dU/dn

τ0 τ

Рис. 9.7. Реограмма жидкости Бингама

Течение Бингамовских жидкостей должно начинаться в точке К, хотя течение реальных ВПЖ начинается в точке А.

Модель Шведова – Бингама:

7

87

vk.com/club152685050 | vk.com/id446425943

Согласно этой модели течение жидкости начинается в точке А при τ>θ, а дальнейшее течение описывается уравнением Бингама.

Вмодели Шведова – Бингама имеются три реологические константы:

θ− статическое напряжение сдвига; τ0 – динамическое напряжение сдвига; η – структурная вязкость.

Статическим напряжением сдвига (СНС) называется касательное напряжение, при превышении которого начинается движение реальной вязкопластичной жидкости или погруженных в нее тел.

Динамическим напряжением сдвига (ДНС) называется касательное напряжение сдвига, при превышении которого началось бы движение ВПЖ или погруженных в нее тел, если бы жидкость подчинялась закону Бингама.

Размерности реологических параметровВПЖ приведены в таблице9.1.

Из рисунка 9.6 видно, что точка К, соответствующая величине ДНС, не лежит на реологической кривой ВПЖ. Величину ДНС невозможно непосредственно измерить, она является математической абстракцией и служит для описания движущейся жидкости (на участке ВС).

Точка А, соответствующая величине СНС, лежит на реологической кривой ВПЖ. Величину СНС можно непосредственно измерить приборами. Она характеризует покоящуюся жидкость.

Реологическая модель Оствальда де-Ваале. Реологическая модель Шведова – Бингама не дает описания криволинейного участка АВ, да и участок ВС не является строго прямым. В англоязычной литературе поведение жидкостей часто описывается уравнением Освальда – де Вааля

8

88