
технология бурения 2
.pdf
vk.com/club152685050 | vk.com/id446425943
Следовательно, для бурения на равновесии на буровой следует иметь две жидкости разной плотности: при бурении использовать жидкость с плотностью, определяемой по зависимости (9.105), а при СПО заполнять скважину более тяжелой жидкостью или производить подъём колонны труб с противодавлением на устье, что возможно при герметичной циркуляционной системе. Бурение на равновесии рентабельно, если эффект от повышения показателей бурения превысит затраты от использования двух промывочных жидкостей.
9.4.Расчет потерь давления при течении бурового раствора
втрубах и кольцевом пространстве
Все элементы циркуляционной системы относительно потерь давления можно разделить на две группы.
Втрубах и кольцевом пространстве потери давления обусловлены трением потока жидкости о стенки канала и пропорциональны длине канала.
Вдругих элементах (замках, задвижках, промывочных отверстиях долота и вертлюге) потери давления связаны с диссипацией энергии из-за резкого изменения величины и направления скорости потока. Потери давления в таких элементах не зависят от длины элемента. Их называют местными сопротивлениями.
Поскольку формулы расчета потерь в местных сопротивлениях очень просты, их иногда используют для расчета потерь давления в элементах, не являющихся, строго говоря, местными сопротивлениями, – в манифольде, стояке, буровом шланге, забойных двигателях.
9.4.1.Расчет потерь давления при течении бурового раствора
втрубах и кольцевом пространстве
Как известно, жидкости могут двигаться в различных режимах. В ламинарном режиме при постоянном расходе скорость жидкости в каждой точке потока постоянна по времени, по величине и по направлению. В турбулентном режиме из-за образования вихрей скорость в каждой точке потока даже при постоянном расходе изменяется и по величине, и по направлению, что обуславливает наличие сил инергии.
9.4.1.1. Расчет потерь давления при течении бурового раствора
втрубах и кольцевом пространстве в ламинарном режиме
Вустановившемся (Q = const) ламинарном режиме скорость течения жидкости в любой точке цилиндрического трубопровода постоянна, т.е.
. Ели жидкость несжимаемая, то и |
, что обуславливает от- |
сутствие сил инерции. Это позволяет получить аналитическое решение для
49
129
vk.com/club152685050 | vk.com/id446425943
зависимости 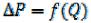 . Известны различные методы получения данной
. Известны различные методы получения данной
зависимости. Одно из них основано на использовании дифференциального уравнения установившегося течения вязкой жидкости.
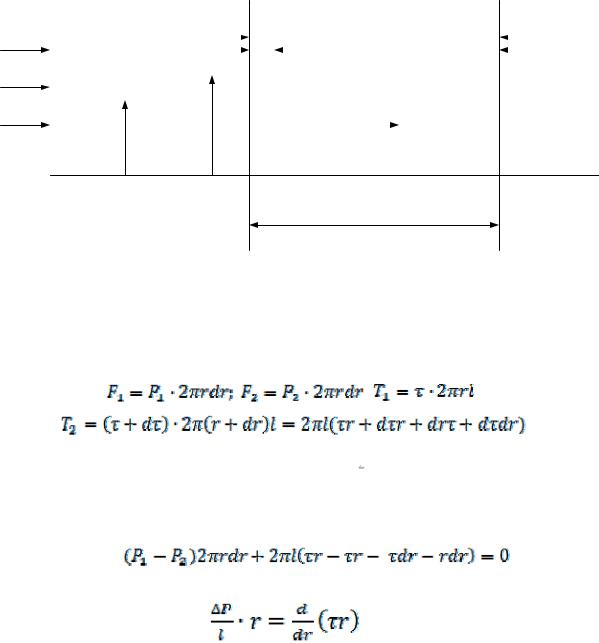
Вывод дифференциального уравнения. Пусть в горизонтальном цилиндрическом трубопроводе в установившемся ламинарном режиме движется несжимаемая жидкость. Выделим в потоке элементарный объем жидкости, ограниченный плоскостями I и II и цилиндрическими поверхностями радиусов r и r + dr (рис. 9.31).
U
|
|
I |
II |
|||||
|
|
|
|
|
|
|
|
|
P1 |
|
|
|
τ +dτ |
|
|
P2 |
|
|
|
|
|
|
||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
||
|
|
|
|
|
|
|||
rr+dr
e
Рис. 9.31. К выводу дифференциального уравнения ламинарного течения жидкости в цилиндрическом трубопроводе
На выделенный объем действуют силы давления и силы вязкого
трения
; |
; |
Последним слагаемым в выражении 


 ввиду его малости можно
ввиду его малости можно
пренебречь. Поскольку установившееся течение и силы инерции малы или отсутствуют, сумма всех внешних сил, действующих на элементарный объем, равна нулю. Отсюда получаем
После упрощения имеем
(9.106)
50
130
vk.com/club152685050 | vk.com/id446425943
Зависимость (9.106) и есть дифференциальное уравнение установившегося течения вязкой несжимаемой жидкости в цилиндрическом трубопроводе. Поскольку при ее выводе не были сделаны какие-либо ограничения по реологическим свойствам жидкости, оно справедливо для жидкостей, описываемых различными реологическими моделями.
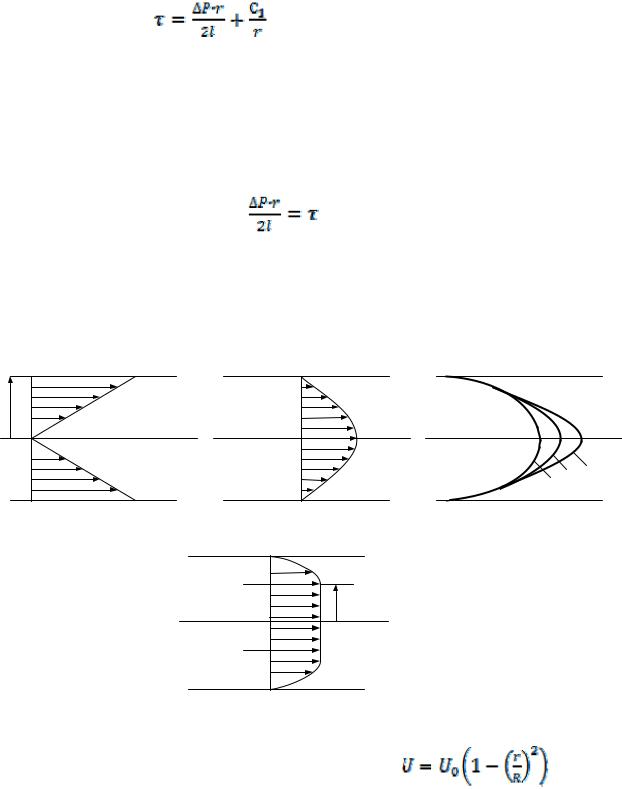
Проинтегрировав уравнение (9.106), получим
(9.107)
Течение жидкостей в трубе радиусом R. Для трубы постоянная ин-
тегрирования С1 в уравнении (9.107) равна нулю, иначе при 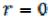 мы по-
мы по-
лучили бы в правой части уравнения бесконечность, что лишено физического смысла. Следовательно, уравнение (9.107) для течения жидкости в трубе имеет вид
(9.108)
Из выражения (9.108) следует, что величина касательных напряжения в жидкости, текущей в ламинарном режиме в трубе, пропорциональна радиусу (рис. 9.32).
|
τ |
|
R |
U0 |
|
|
|
|
|
|
0,4 0,5 0,8 |
а) |
б) |
в) |
|
U0 |
r0 |
|
г) |
Рис. 9.32. Эпюры касательных напряжений (а) и профили скоростей при
ламинарном течении в трубе: б – ньютоновской ( |
), |
51
131
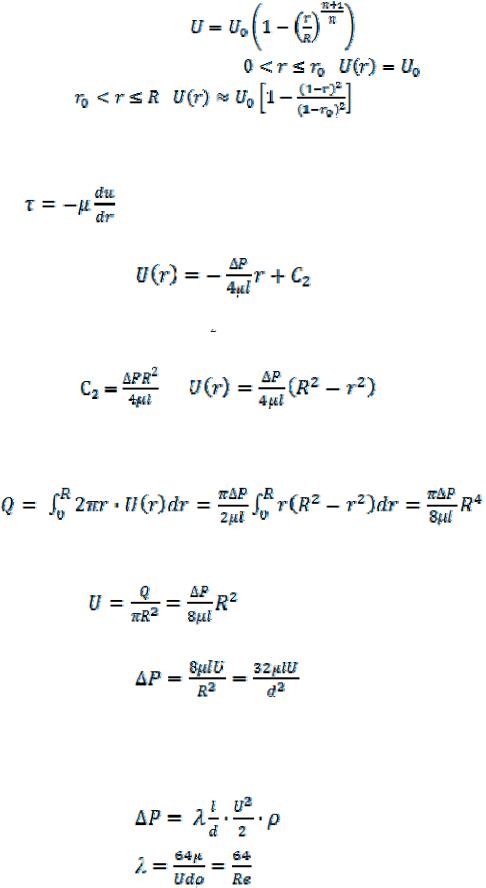
vk.com/club152685050 | vk.com/id446425943 |
|
в – степенной ( |
), |
г – бингамовской жидкости ( |
; |
|
) |
а) Пусть в трубе движется ньютоновская жидкость, реологическое уравне-
ние которой |
. Подставив его в (9.108), после интегрирования |
получим
(9.109)
Постоянную интегрирования 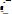

 найдем из граничного условия – при
найдем из граничного условия – при
r = R.
U(r) = 0, тогда |
и |
(9.110) |
Из (9.110) следует, что при ламинарном течении ньютоновской жидкости в трубе скорость по сечения трубы изменяется по закону параболы. Найдем расход жидкости
(9.111)
Средняя скорость течения жидкости
(9.112)
Отсюда
(9.113)
где d = 2R – диаметр трубы.
Уравнение (9.113) есть уравнение Пуазейля. Приведем его к стандартному виду уравнения Дарси – Вейсбаха, для чего умножим и разделим правую часть на 2ρU. В результате получим
(9.114)
(9.115)
52
132

vk.com/club152685050 | vk.com/id446425943
б) Если в трубе движется степенная жидкость, описываемая уравнением Оствальда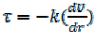 , то, подставляя его в уравнение (9.108), аналогично
, то, подставляя его в уравнение (9.108), аналогично
предыдущему получим
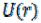 =
=
(9.116)
Его также можно привести к уравнению Дарси – Вейсбаха (9.114),
где
(9.117)
в) Если в трубе движется жидкость Бингама ( и
и
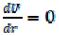 при
при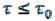 ), то, аналогично пункту а, получим
), то, аналогично пункту а, получим
,
(9.118)
где .
(9.119)
, |
(9.120) |
53
133
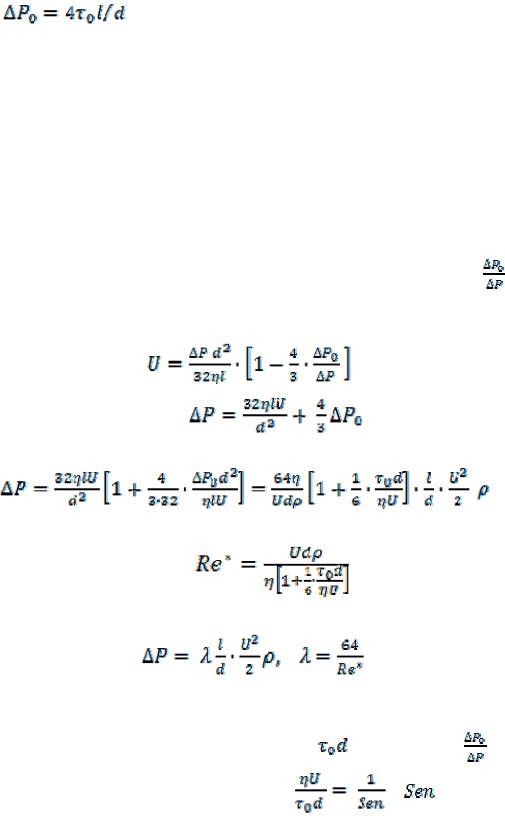
vk.com/club152685050 | vk.com/id446425943
где .
Из (9.118) следует, что в центральной части трубы, при 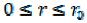 , жидкость Бенгама движется с постоянной скоростью
, жидкость Бенгама движется с постоянной скоростью 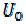 с неразрушенной структурой и лишь на периферии потока скорость изменяется от
с неразрушенной структурой и лишь на периферии потока скорость изменяется от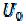 до ну-
до ну-
ля. Поэтому в литературе ламинарный режим течения ВПЖ Бингама часто называют структурным (рис. 9.33).
Уравнения (9.119), (9.120) называются уравнениями Букингама. Существуют различные методы разрешения уравнения Букингама
относительно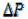 .
.
Приближенное решение уравнений Букингама. При <0,5 по-
следним членом в квадратных скобках уравнения Букингама можно пренебречь (ошибка при этом будет не больше 2,3 %). Тогда из упрощенного
уравнения Букингама |
получим |
(9.121)
Его также можно преобразовать к виду уравнеия Дарси – Вейсбаха. (9.122)
Введем обобщенный параметр Рейнольдса ВПЖ
(9.123)
Тогда зависимость (9.122) примет вид
(9.124)
Решение уравнения Букингама без такого упрощения. По И. Х.
Гродде приведем уравнения (9.119), (9.120) к безразмерному виду. Для |
|||
этого умножим обе части уравнения на / |
и обозначим |
= β. Тогда |
|
левая часть уравнения будет иметь вид |
, |
– параметр Сен- |
|
Венана. |
|
|
|
54
134
vk.com/club152685050 | vk.com/id446425943
|
|
|
|
I |
|
II |
|||||||||
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P1 |
|
|
|
|
τ +dτ |
|
|
|
P2 |
|
H |
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
τ |
h+dh |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ι
Рис. 9.33. К выводу дифференциального уравнения ламинарного течения жидкости в плоской щели
Множитель перед квадратной скобкой в правой части уравнения будет равен
Тогда уравнение Букингама будет приведено к виду
(9.125)
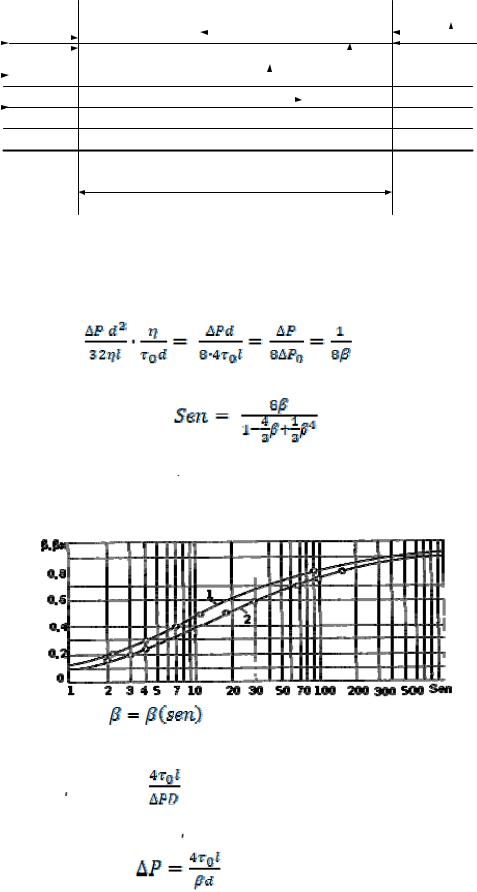
График зависимости 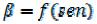 согласно уравнению (9.125) показан на рисунке 9.34.
согласно уравнению (9.125) показан на рисунке 9.34.
Рис. 9.34. Зависимость |
для труб круглого (1) и кольцевого (2) |
|
сечений |
Поскольку  =
= 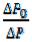 = , зная величину параметра Сен-Венана, по кривой 1 определяется величина
= , зная величину параметра Сен-Венана, по кривой 1 определяется величина  , а затем уже перепад давления
, а затем уже перепад давления
(9.126)
55
135
vk.com/club152685050 | vk.com/id446425943
Течение жидкости в концентричном кольцевом пространстве как в плоской щели. Для кольцевого пространства в уравнении (9.107) постоянная интегрирования С1 не равна нулю, что существенно усложняет выкладки.
Задача упрощается, если учесть, что зависимость перепада давления от средней скорости течения жидкости в узком кольцевом пространстве, при D/d = R2/R1 < 2, равна такой же зависимости для плоской щели шири-
ной 2H = R2–R1 (рис. 9.35).
du/dr |
Q |
|
n, об/мин. |
||
|
600
300 |
|
|
|
3 |
|
4 |
2 |
2 |
1 |
3 |
1 |
|
|
||
|
|
|
|
τ0 |
τ |
ΔP0 3/4ΔP0 |
Р |
|
а) |
|
б) |
Рис. 9.35. Сопоставление реограмм жидкостей Бингама и Оствальда и зависимостей , полученных из этих моделей с фактическими зави-
симостями: а) реограммы жидкостей Бингама (1), Оствальда (2) и реальной
ВПЖ (3); б) зависимости |
согласно полному (1) и упрощённому |
(2) уравнению Букингама и уравнение для степенной жидкости (3), фактическая зависимость (4)
Дифференциальное уравнение установившегося течения жидкости в плоской щели при ламинарном режиме (из условия равенства суммы всех внешних сил нулю) имеет вид
, |
(9.127) |
его интегрирование дает
(9.128)
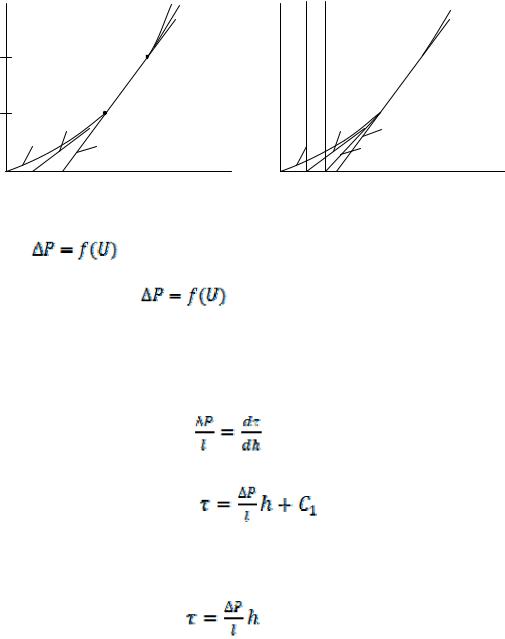
Но для плоской щели С1 равен нулю, следовательно, распределение касательных напряжений по сечению щели будет описываться выражением
(9.129)
Подставляя в уравнение (9.129) реологические уравнения и переходя от H
к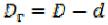 , получаем
, получаем
а) для ньютоновской жидкости уравнение Буссинеска:
56
136
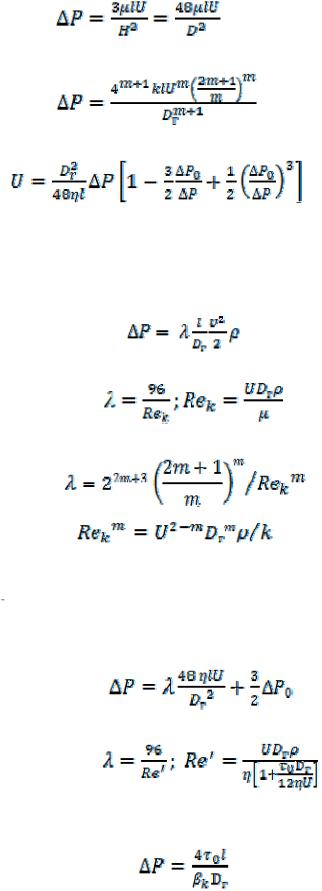
vk.com/club152685050 | vk.com/id446425943
(9.130)
б) для степенной жидкости:
(9.131)
в) для жидкости Бингама:
, |
(9.132) |
где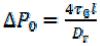 .
.
Уравнения (9.130) и (9.131) легко приводятся к виду уравнения Дарси – Вейсбаха
,
где для ньютоновской жидкости:
(9.133)
для жидкости Освальда:
(9.134)
Уравнение (9.132) имеет приближенное и точное решения.
При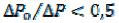 последним членом в квадратных скобках можно пренебречь. Получим линейное относительно
последним членом в квадратных скобках можно пренебречь. Получим линейное относительно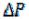 уравнение, которое легко разрешается:
уравнение, которое легко разрешается:
(9.135)
Его также можно привести к виду уравнения Дарси – Вейсбаха, где
(9.136)
Как и уравнение Букингама, выражение (9.132) может быть приведено к виду
, |
(9.137) |
где
57
137

vk.com/club152685050 | vk.com/id446425943
(9.138)
График функции (9.138) показан на рисунке 9.34 (линия 2).
О точности полученных формул. Для ламинарного течения вязкопластичной жидкости нами получены три зависимости перепада давления от средней скорости течения (расхода), полное и упрощенное уравнения Букингама (для модели Бингама) и уравнение для степенной модели.
При малых значениях градиента скорости сдвига модель Бингама завышает, а модель Оствальда занижает значения касательных напряжений (рис. 9.35 а). Поэтому при малых расходах уравнение Букингама завышает, а уравнение для степенной жидкости занижает величины перепада давления (рис. 9.35 б). Наибольшее завышение дает упрощенное уравнение Букингама. При более высоких градиентах скорости сдвига реограммы теоретических моделей близки к фактической, поэтому при высоких расходах (в пределах ламинарного течения) и уравнение Букингама, и уравнение для жидкости Оствальда должны давать значения перепадов давлений, близкие к фактическим.
9.4.1.2 Расчет потерь давления при турбулентном течении жидкостей
в трубах и кольцевом пространстве
Исследованиями Гагена и О. Рейнольдса было установлено, что жидкости могут двигаться в разных режимах – ламинарном, когда силы инерции много меньше сил вязкости, и турбулентном, когда силы инерции преобладают. Число критериев подобия, характеризующих режим течения, равно числу параметров реологической модели. Для ньютоновской жидкости, имеющей один реологический параметр  , имеется один критерий подобия
, имеется один критерий подобия
– параметр Рейнольдса |
. У жидкости Бингама с двумя реоло- |
гическими константами 


 и
и 
 режим течения характеризуется двумя критериями подобия – Рейнольдса
режим течения характеризуется двумя критериями подобия – Рейнольдса  и Хедстрема
и Хедстрема  .
.
Режим течения жидкости Оствальда определяется параметром 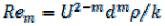 и показателем нелинейности m.
и показателем нелинейности m.
Критические значения параметров Re для различных жидкостей приведены в табл. 9.4, а значения коэффициентов местных сопротивлений
– в табл. 9.5.
58
138
