Задание на выполнение работы
Используя вариационный и статистический ряды, определить выборочные числовые характеристики: среднее значение, смещенную и несмещенную дисперсии, среднее квадратическое отклонение, показатели асимметрии и эксцесса. Сравнить друг с другом значения числовых характеристик, вычисленные для вариационного и статистического рядов. Обратить внимание на разницу между смещенной и несмещенной дисперсией.
Порядок выполнения работы
1. Дополнить программу, составленную на предыдущих занятиях, блоком для вычисления выборочных числовых характеристик.
2. Отладить программу и определить выборочные числовые характеристики для Вашей выборки.
3. Сделать выводы по работе. Обратите внимание на форму гистограммы и значения показателей асимметрии и эксцесса.
Контрольные вопросы
1. Запишите формулу начального момента второго порядка для вариационного ряда; для статистического ряда.
2. Что понимается под выборочным средним значением?
3. Как вычислить центральный момент третьего порядка для вариационного ряда? Для статистического ряда?
4. Запишите формулы для смещенной и несмещенной дисперсии.
5. Как определить среднее квадратическое отклонение?
6. Что характеризуют асимметрия и эксцесс?
7. Как повысить точность вычислений центральных моментов второго и более старшего порядков?
Лабораторная работа №4 проверка выборки на соответствие нормальному закону
Цель работы
Изучение методики оценки соответствия выборок нормальному закону распределения случайных величин.
Краткая теория
Законом распределения называют связь между возможными значениями случайной величины и вероятностями их появления.
Для количественной характеристики закона распределения служат две функции: функция (интегральная) распределения F(x) и плотность (дифференциальная функция) распределения f(x).
Случайные величины могут иметь разные законы распределения. Установление закона, которому подчиняется конкретная выборка, очень важно для определения ее характеристик.
Правильному выбору того или иного закона помогает графическое изображение гистограммы и плотности вероятности, соответствующей выбранному закону распределения (см. рис.4.1).
В работах при статистическом оценивании характеристик распределений пользуются следующими понятиями:
1. Гипотезы (статистические) – различного рода предположения о законах распределения рассматриваемых случайных величин.
2. Нуль-гипотеза
(общепринятое обозначение –
)
–
гипотеза, справедливость которой
подвергается испытанию. Предположение,
являющееся логическим отрицанием
проверяемой нуль-гипотезы
,
называется альтернативной
(конкурирующей) гипотезой
(обозначение
).
3. Критерий (статистический) – решающее правило, по которому на основе результатов наблюдений (выборки) принимается решение в задаче статистической проверки гипотез.
4. Уровень значимости – вероятность ошибочного отклонения нулевой гипотезы . Например уровень значимости, равный 0.05, означает, что в среднем в пяти случаях из ста ошибочно отвергают высказанную гипотезу.
5. Число
степеней свободы
определяется как разность между числом
полученных данных (например, объемом
выборки или числом классов в статистическом
ряду) и числом вычисленных с этими
данными статистических характеристик.
Предположим, с данными выборки объемом
n
были вычислены две величины: среднее и
выборочная дисперсия, тогда
.
,
Теоретический закон
распределения
Гистограмма
x
Рис. 4.1. Сравнение гистограммы с выбранной теоретической кривой
распределения.
Нормальный закон распределения (закон Гаусса) является одним из наиболее распространенных. По этому закону плотность распределения непррывной случайной величины связана с величиной x соотношением:
,
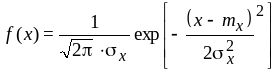(4.1)
где
- математическое ожидание,
и
–
генеральные дисперсия и среднее
квадратическое отклонение величины X.