
- •1Цели работы:
- •2Приборы и принадлежности:
- •3Описание установки.
- •4Подготовка прибора к работе
- •5Порядок выполнения работы
- •6Уравнение динамики твердого тела, вращающегося вокруг движущейся оси
- •7Диск максвелла
- •8Теория работы
- •9Момент инерции сплошного диска
- •10Вопросы для самопроверки.
- •11Задачи для самостоятельного решения
- •12Литература
8Теория работы
На данной установке можно провести
прямые измерения времени движения диска
Максвелла на заданном расстоянии
![]() ,
причем движение начинается из состояния
покоя. Величины
и
также доступны непосредственному
измерению и мы будем считать их известными.
Следовательно, в формулу (7.4) входят три
неизвестных величины:
,
причем движение начинается из состояния
покоя. Величины
и
также доступны непосредственному
измерению и мы будем считать их известными.
Следовательно, в формулу (7.4) входят три
неизвестных величины:
![]() .
Ускорение
,
однако, легко может быть найдено по
времени движения
.
Ускорение
,
однако, легко может быть найдено по
времени движения
![]() и пройденному расстоянию
,
т.к. в соответствии с (7.4) при сделанных
предположениях
постоянно. Поскольку начальная скорость
равна нулю, то в идеально функционирующей
установке мы имели бы
и пройденному расстоянию
,
т.к. в соответствии с (7.4) при сделанных
предположениях
постоянно. Поскольку начальная скорость
равна нулю, то в идеально функционирующей
установке мы имели бы
![]() и
и
![]() .
К сожалению, из-за конструктивных
особенностей установки отсчет времени
начинается не сразу в момент начала
движения, а тогда, когда система сместится
на некоторое расстояние
.
К сожалению, из-за конструктивных
особенностей установки отсчет времени
начинается не сразу в момент начала
движения, а тогда, когда система сместится
на некоторое расстояние
![]() ,
равное, по нашим оценкам, примерно 3 мм.
На первый взгляд кажется, что если,
например, высота, проходимая диском,
составляет
=30
см , то поскольку
,
равное, по нашим оценкам, примерно 3 мм.
На первый взгляд кажется, что если,
например, высота, проходимая диском,
составляет
=30
см , то поскольку
![]() ,
т.е. примерно 1 % , то погрешностью в
определении ускорения по формуле
можно вполне пренебречь. Однако на самом
деле это не так. Начав движение из
состояния покоя система в конце участка
приобретает скорость
,
т.е. примерно 1 % , то погрешностью в
определении ускорения по формуле
можно вполне пренебречь. Однако на самом
деле это не так. Начав движение из
состояния покоя система в конце участка
приобретает скорость
![]() .
Тогда для оставшегося участка длиной
.
Тогда для оставшегося участка длиной
![]() можно записать
можно записать
![]() ,
,
где — время движения на этом участке, которое и измеряется на установке. Тогда
![]() .
.
Решая это уравнение относительно
![]() ,
находим
,
находим
![]() .
(8.1)
.
(8.1)
При указанных выше численных значениях
имеем
![]() и относительная погрешность в определении
величины
по формуле
составляет уже не 1 % , а целых 20 % , что
слишком много, если учесть точность, с
которой измеряется время движения и
расстояние, проходимое диском. На уровне
относительной погрешности 1 % ускорение
следует определять по формуле
и относительная погрешность в определении
величины
по формуле
составляет уже не 1 % , а целых 20 % , что
слишком много, если учесть точность, с
которой измеряется время движения и
расстояние, проходимое диском. На уровне
относительной погрешности 1 % ускорение
следует определять по формуле
![]() ,
(8.2)
,
(8.2)
где мы пренебрегли величиной
![]() по сравнению с единицей. Таким образом,
в формулу
по сравнению с единицей. Таким образом,
в формулу
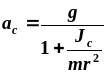 (8.3)
(8.3)
входят две величины
![]() и
,
которые непосредственно не определяются.
Конечно, значение ускорения свободного
падения
хорошо известно из других опытов и
составляет примерно
и
,
которые непосредственно не определяются.
Конечно, значение ускорения свободного
падения
хорошо известно из других опытов и
составляет примерно
![]() .
Тогда из формулы (8.3) можно определить
момент инерции
и сравнить полученное значение с
результатом, рассчитанным по теоретическим
формулам.
.
Тогда из формулы (8.3) можно определить
момент инерции
и сравнить полученное значение с
результатом, рассчитанным по теоретическим
формулам.
Применим метод наименьших квадратов. Вначале линеаризируем исследуемую зависимость. Приравнивая правые части формул (8.2) и (8.3), получим
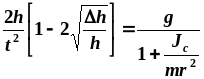
или
![]() (8.4)
(8.4)
Вводя обозначения
![]()
![]() и
и
![]()
уравнение (8.4) можно переписать в виде линейного уравнения
![]() (8.5)
(8.5)
Составляя сумму
![]() ,
(8.6)
,
(8.6)
определим параметр А из условия минимума суммы (8.6):
![]()
Решая полученную систему линейных уравнений, находим значение параметра А:
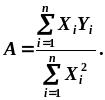 (8.7)
(8.7)
Зная значение параметра А, можно определить значение момента инерции диска Максвелла и сменной накладки.
