Постоянный электрический ток

Сила постоянного тока

I = q/t,

где q – заряд, прошедший через поперечное сечение проводника за время t.

Плотности тока

j = I/S,

где S – площадь поперечного сечения проводника.

Связь плотности тока со средней скоростью <υ> направлен­ного движения заряженных частиц

j = qn<υ>,

где q – заряд частицы; n – концентрация заряженных частиц.

Закон Ома:

а) для участка цепи, не содержащего ЭДС, где φ₁ – φ₂ = U – разность потенциалов (напряжение) на концах участка цепи; R – сопротивление участка;

б) для участка цепи, содержащего ЭДС, где – ЭДС источника тока; R – полное сопротивление участка (сумма внешних и внутренних сопротивлений);

в) для замкнутой (полной) цепи, где R – внеш­нее сопротивление цепи; R_i – внутреннее сопротивление цепи.

Законы Кирхгофа:

а) ∑ I_i = 0 – первый закон;

б) ∑ I_iR_i = ∑ – второй закон,

где ∑ I_i – алгебраическая сумма сил токов, сходящихся в узле; ∑ I_iR_i – алгебраическая сумма произведений сил токов на сопротивление уча­стков; ∑ _i – алгебраическая сумма ЭДС.

Сопротивление R и проводимость G проводника

R = ρl/S, G=γS/l,

где ρ – удельное сопротивление; γ – удельная проводимость; l – длина проводника; S – площадь поперечного сечения проводника.

Сопротивление системы проводников:

а) R = ∑ R_i при последовательном соединении;

б) 1/R = ∑(1/R_i) при параллельном соединении, где R_i – сопро­тивление i-го проводника.

Работа тока

A = IUt, A = I²Rt, A = U²t/R.

Первая формула справедлива для любого участка цепи, на кон­цах которого поддерживается напряжение U, последние две – для уча­стка, не содержащего ЭДС.

Мощность тока

P = IU, P = I²R, P=U²/R.

Закон Джоуля – Ленца

Q = I²Rt.

Закон Ома в дифференциальной форме

= γ ,

где γ – удельная проводимость; – напряженность электрического поля; – плотность тока.

П ример 1. Потенциометр сопротивлением R = 100 Ом под­ключен к батарее с ЭДС  = 150 В и внутренним сопротивлением R_i = 50 Ом. Определить: 1) показание вольтметра между сопротивлением R_v = 500 Ом, соеди­ненного с одной из клемм потенциометра и подвижным контактом, установленным посе­редине потенциометра; 2) разность потен­циалов между теми же точками потенцио­метра при отключении вольтметра.

Р е ш е н и е. 1. Показание вольт­метра, подключенного к точкам А и В (рис. 12), определим по формуле

U₁ = I₁R₁,

где R₁ – сопротивление параллельно соединенных вольтметра и поло­вины потенциометра; I₁ – суммарная сила тока в ветвях этого соедине­ния (она равна силе тока в неразветвленной части цепи).

Силу тока I₁ найдем по закону Ома для полной цепи:

I₁ =  /(R_e +R_i), (1)

где R_e – сопротивление внешней цепи. Это сопротивление есть сумма двух сопротивлений:

R_e = R/2 +R₁. (2)

Сопротивление R₁ найдем по формуле параллельного соедине­ния проводников откуда

Подставив в (1) выражение R_e по (2), найдем

В данном случае решение задачи в общем виде было бы гро­моздким. Поэтому удобно вычисление величин провести раздельно:

U₁ = 1,03·45·5 В = 46,9 В.

2. Разность потенциалов между точками А и В при отключен­ном вольтметре равна произведению силы тока I₂ на половину сопро­тивления потенциометра:

U₂ = I₂ ·R/2, (3)

где I₂ – сила тока в цепи при отключенном вольтметре. Ее определим по формуле

I₂ =  /(R + R_i).

Подставив выражение I₂ в (3), найдем

U₂ =  / (R + R_i)·R/2.

Произведем вычисления:

П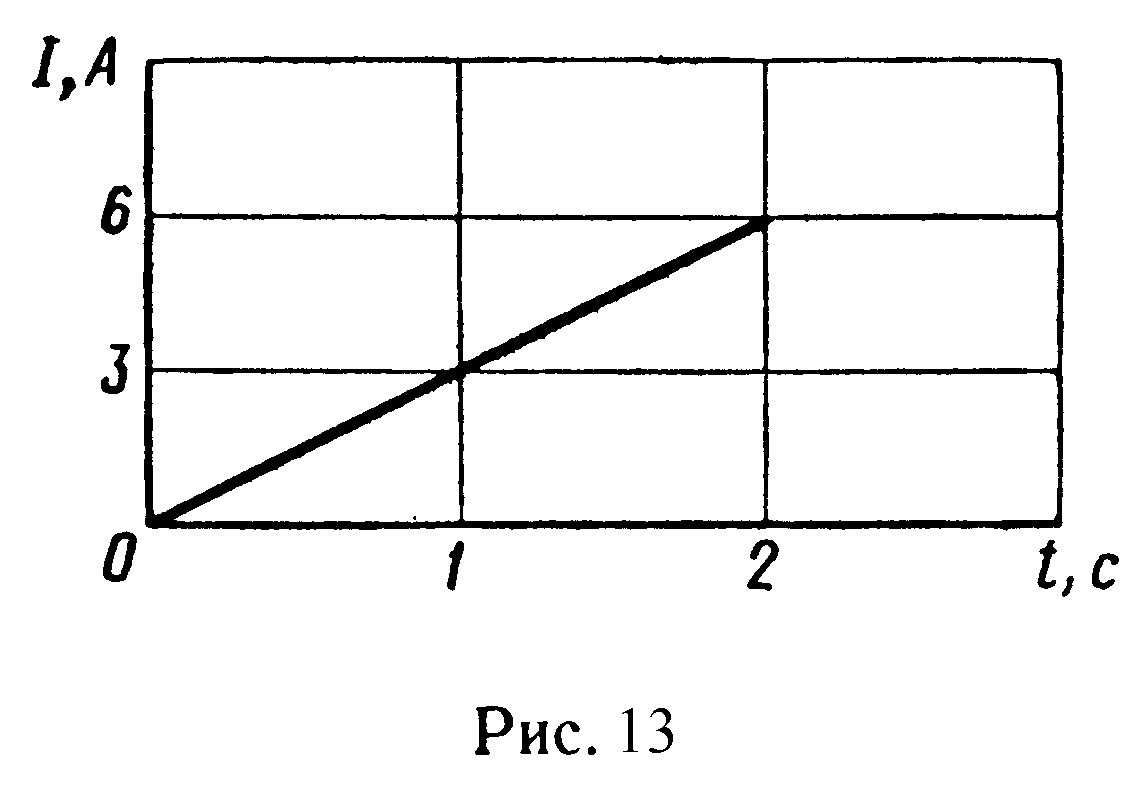 ример 2. Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Δt = 2 с по линейному закону от I₀ = 0 до I = 6 А (рис 13). Определить теплоту Q₁, выделившуюся в этом проводнике за первую секунду, и Q₂ – за вторую, а также найти отношение q₁/q₂.

Р е ш е н и е. Закон Джоуля – Ленца в виде Q = I²Rt справедлив для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон спра­ведлив для бесконечно малого интервала времени и записывается в виде

dQ = I²Rdt. (1)

Здесь сила тока I является некоторой функцией времени. В данном случае

I = kt, (2)

где k – коэффициент пропорциональности, характеризующий скорость изменения силы тока:

С учетом (2) формула (1) примет вид

dQ = k²Rt²dt. (3)

Для определения теплоты, выделившейся за конечный интер­вал времени Δt, выражение (3) надо проинтегрировать в пределах от t₁ до t₂:

Произведем вычисления:

Q₁ = 1/3 · 3² · 20(1 – 0) Дж = 60 Дж;

Q₂ = 1/3 · 3² · 20(8 – 1) Дж = 420 Дж.

Следовательно,

Q₂ / Q₁ = 420 / 60 = 7,

т. е. за вторую секунду выделится теплоты в семь раз больше, чем за первую.

Пример 3. Пространство между пластинами плоского конден­сатора имеет объем V = 375 см³ и заполнено водородом, который час­тично ионизирован. Площадь пластин конденсатора S = 250 см². При каком напряжении U между пластинами конденсатора сила тока I, про­текающего через конденсатор, достигнет значения 2мкА, если концен­трация n ионов обоих знаков в газе равна 5,3 · 10⁷ см^–3. Принять под­вижность ионов b₊= 5,4 · 10 ^–4 м² / (В · с), b_-=7,4 · 10^-4 м²/(В · с).

Р е ш е н и е. Напряжение U на пластинах конденсатора свя­зано с напряженностью Е электрического поля между пластинами и расстоянием d между ними соотношением

U = Ed. (1)

Напряженность поля может быть найдена из выражения плот­ности тока

j = qn(b₊ + b_-)E,

где q – заряд иона.

Отсюда

Расстояние d между пластинами, входящее в формулу (1), най­дем из соотношения

d = V/S.

Подставив выражения Е и d в (1), получим

(2)

Проверим, дает ли правая часть полученной расчетной фор­мулы единицу напряжения:

Подставим в формулу (2) значения величин и произведем вы­числения: