
- •Министерство образования и науки Российской Федерации
- •Архангельск
- •Рекомендации по решению задач контрольных работ
- •Основные теоретические сведения
- •Относительность движения. Система отсчета.
- •В декартовой системе координат такой радиус-вектор может быть представлен следующим образом:
- •Кинематика материальной точки
- •При постоянном угловом ускорении угловая скорость
- •Динамика поступательного движения
- •Первый закон Ньютона.
- •Второй закон Ньютона. Сила. Масса.
- •Замкнутые системы. Закон сохранения импульса.
- •Центр масс. Теорема о движении центра масс.
- •Работа и мощность в механике.
- •Кинетическая энергия материальной точки и механической системы
- •Консервативные и неконсервативные силы.
- •Потенциальная энергия
- •Закон сохранения механической энергии
- •Динамика вращательного движения твердого тела
- •Момент силы и момент импульса
- •Закон сохранения момента импульса
- •Момент инерции. Теорема Штейнера.
- •Моменты инерции некоторых однородных симметричных тел
- •Основное уравнение динамики вращательного движения
- •Кинетическая энергия и работа при вращательном движении абсолютно твердого тела
- •Работа при повороте твердого тела относительно произвольной неподвижной оси z на некоторый угол φ под действием внешних сил Мz
- •Примеры решения задач
- •Поэтому, учитывая, что
- •По третьему закону Ньютона
- •Проверим размерность
- •Произведем расчет
- •Варианты контрольной Работы
- •Задачи для самостоятельного решения
- •Рекомендуемая литература
- •Оглавление
Замкнутые системы. Закон сохранения импульса.
Система, на которую не действуют внешние силы, называется замкнутой. В таких системах выполняется закон сохранения импульса, согласно которому векторная сумма импульсов тел замкнутой системы является величиной постоянной:
![]()
Для
частного случая замкнутой системы,
состоящей из двух тел, имеющих до
взаимодействия импульсы
![]() и
и
![]() ,а после взаимодействия импульсы
,а после взаимодействия импульсы
![]() и
и
![]() соответственно, закон сохранения
импульса запишется в следующем виде :
соответственно, закон сохранения
импульса запишется в следующем виде :
+ = +
Отметим также, что если система не является замкнутой, т.е. векторная сумма внешних сил, действующих на систему, не равна нулю
![]() ,
,
но проекция этой суммы сил на некоторое направление, например, на произвольную ось х, равна нулю
![]() ,
,
то проекция импульса такой системы на это направление является величиной постоянной:
![]()
Центр масс. Теорема о движении центра масс.
Центром
масс (или центром инерции) системы
называется точка, радиус-вектор
![]() которой выражается через радиус-векторы
которой выражается через радиус-векторы
![]() ,
,
![]() ,
… ,
,
… ,
![]() и массы m1, m2
, … , mn
материальных точек такой системы по
формуле
и массы m1, m2
, … , mn
материальных точек такой системы по
формуле
=
![]() ,
,
где m = m1 + m2 + … + mn – масса этой системы.
Согласно
теореме о движении центра масс, центр
масс системы движется как материальная
точка, масса которой равна суммарной
массе m всей системы, под
действием силы, равной геометрической
сумме сил
![]() , действующих на эту систему :
, действующих на эту систему :
![]() ,
,
где
![]() - скорость центра масс.
- скорость центра масс.
Отметим, что центр масс замкнутой системы движется равномерно и прямолинейно или покоится.
Работа и мощность в механике.
Р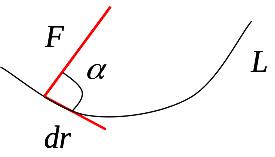 аботой
А силы
на произвольной по форме траектории L
(рис. 5)
аботой
А силы
на произвольной по форме траектории L
(рис. 5)
называется криволинейный интеграл A=
Подинтегральное
выражение в последней формуле является
скалярным произведением
![]()
![]() ).
).
Рис.5
вектора на элементарно малое перемещение и называется элементарной работой:
![]() A=(
)
= Fdr
cos
A=(
)
= Fdr
cos
![]() ,
,
где - угол между векторами и .
Как известно из аналитической геометрии
( ) =Fxdx+Fydy+Fzdz,
где Fx, Fy, Fz - проекции силы , а dx, dy, dz - проекции перемещения на оси координат x, y, z соответственно.
Поэтому работу А можно рассчитать следующим образом:
![]()
В СИ работа выражается в джоулях (Дж).
1 Дж = 1Н · 1 м
Мощность N характеризует быстроту выполнения работы в течение времени t :
N
=
![]()
При перемещении материальной точки (или тела) под действием постоянной силы со скоростью мощность определяется по формуле
N = (![]() )
)
В СИ мощность выражается в ваттах (Вт) .
1 Вт = 1 Дж/1с
Кинетическая энергия материальной точки и механической системы
Кинетическая энергия Т определяется скоростью материальных точек механической системы.
Материальная точка массой m, движущаяся со скоростью , обладает кинетической энергией
Т =
![]()
Кинетическая энергия Т механической системы равна сумме кинетических энергий ее материальных точек:
Т =
![]()
где
m1
,
m2
,…, mn
– массы, а
![]() ,
,
![]() ,
…,
,
…,
![]() - скорости материальных точек системы.
- скорости материальных точек системы.
Работа А всех сил, действующих на механическую систему при её перемещении, равна приращению кинетической энергии ΔТ этой системы:
А= ΔТ=Т2-Т1,
где Т2 - кинетическая энергия системы в конечном, а Т1 - в начальном состоянии.
Кинетическая энергия выражается в тех же единицах, что и работа, т.е. в джоулях.
