Приложение.
При
вычислении погонных параметров линии
мы не будем учитывать, для упрощения
задачи, влияние одного провода на другой,
полагая
.
Это обстоятельство позволяет считать,
что распределение тока и заряда в каждом
проводнике обладает осевой симметрией.
Вычислим сначала емкость и индуктивность
единицы длины линии без потерь, считая
проводники идеально проводящими.
Начнем с емкости.
Пусть
полный заряд единицы длины одного
провода равен
(
другого -
).
Задача сводится к вычислению разности
потенциалов проводов. Электрическое
поле одного провода в точке
на
расстоянии
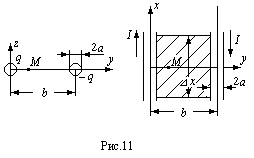
от его оси (смотри рисунок 11 )
.
Поле двух проводов в точке
,
Разность
потенциалов
Наконец,
емкость
( 1 )
При
вычислении индуктивности единицы
длины линии задача сводится к вычислению
магнитного потока через заштрихованную
на рис. 11 площадь. Она представляет
маленькую часть длиной
очень длинного контура с током. Легко
по-нять,что провода создают одинаковые
потоки, поэтому достаточно вычислить
поток от одного провода и результат
удвоить. Магнитная индукция одного
провода с током
в точке
на расстоянии
от оси провода, перпендикулярна плоскости
площадки и равна
Поток
магнитной индукции
Искомая
индуктивность
( 2 )
Укажем,
для сравнения, точный результат, который
получится с учетом взаимного влияния
проводов. Надо просто заменить аргумент
логарифмической функции в формулах для
и
на следующий:
Теперь перейдем к реальным проводникам и вычислим приближенно сопротивле-ние и внутреннюю индуктивность единицы длины линии с учетом скин-ффекта.
Сопротивление
считаем следующим образом. Пока
скин-эффект выражен слабо и
,
мы его не учитываем, считая сопротивление,
как на постоянном токе. Множи-тель 2
учитывает второй провод.
( 3 )
Когда
скин-эффект выражен сильно (
),
мы используем модель Рэлея и считаем,
что весь ток равномерно распределен
только в кольцевой области толщиной
вблизи поверхности проводника (токовая
трубка), с площадью сечения
Тогда
( 4 )
Получается очень неплохое приближение.
Внутреннюю
индуктивность считаем для одного
провода. Индуктивность линии будет в
два раза больше. Рассмотрим опять два
случая. Скин-эффект выражен слабо,
.
Предполагая распределение тока по
сечению проводника равномерным, пишем
магнитную индукцию внутри проводника
на расстоянии
от оси.
Здесь
- объемная плотность тока в проводнике.
Магнитный поток единицы длины одного
провода
Отсюда
( 5 )
Как для постоянного тока.
Скин-эффект
выражен сильно,
.
Теперь предполагаем равномерное
распре-деление тока только в кольцевой
области толщиной
и
сечением
,
примы-кающей к поверхности. Внутри поля
и тока нет. Тогда, при
,
получим
,
где
- плотность тока в кольцевой области.
В итоге (
):
( 6 )
В
заключение приведем некоторые оценки
параметров линии для медных и железных
проводников:
0,3 мм;
1,5 мм;
;
33
пф;