
- •Побудуємо математичну модель початкової задачі
- •Побудуємо математичну модель двоїстої задачі
- •Розв’яжемо початкову злп симплекс-методом:
- •Розв’язання початкової та двоїстої злп в середовищі Excel
- •Дамо економічне тлумачення основним та додатковим змінним початкової та двоїстої задач, а також значення їхніх цільових функцій.
- •Визначимо дефіцитні та недефіцитні ресурси. Розрахуємо межі зміни дефіцитних ресурсів.
- •Визначимо рентабельну та нерентабельну продукцію.
- •Розрахуємо доцільність розширення асортименту за рахунок введення нової продукції.
- •Врахування обмежень попиту на продукцію
Визначимо дефіцитні та недефіцитні ресурси. Розрахуємо межі зміни дефіцитних ресурсів.
Через
значення додаткових змінних початкової
задачі ми бачимо, що третій ресурс є
дефіцитним (оскільки
 ),
а перший та другий – недефіцитні, бо
їхні значення не дорівнюють нулю (
),
а перший та другий – недефіцитні, бо
їхні значення не дорівнюють нулю ( ).
).
Для
розрахунку інтервалів можливої зміни
обсягів дефіцитних ресурсів, у межах
яких двоїсті оцінки уі
залишаються
на рівні оптимальних значень, позначимо
приріст (зміну) запасу третього ресурсу
через
 Тоді новий оптимальний план можна
записати у такий спосіб:
Тоді новий оптимальний план можна
записати у такий спосіб:
Х*
=
( ;
;
1000+
;
;
1000+ )
)
Єдина вимога, що має виконуватись – це умова невід’ємності змінних:



Це означає, що коли запас третього ресурсу збільшиться на 2000 одиниць або зменшиться на 6993 одиниці, то на цьому інтервалі його оптимальна двоїста оцінка залишиться у3=6,4. Отже, запас третього ресурсу може змінюватися в межах:
7000-6993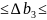 7000+2000
7000+2000
7 9000
Згідно з цим максимально можливі зміни обсягів виручки підприємства залежно від змін у постачанні ресурсу 3 на такому інтервалі будуть в межах:
45000-6993 6,4
6,4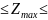 45000
45000 2000
6,4
2000
6,4
244,8 57800
Визначимо рентабельну та нерентабельну продукцію.
Аналізуючи
додаткові змінні оптимального плану
двоїстої задачі, можемо зробити висновок,
що продукція В рентабельна, оскільки
 .
Аналогічно
робимо висновок, що продукція А, С та D
нерентабельна,
бо значення відповідних їм двоїстих
оцінок оптимального плану двоїстої
задачі
.
Аналогічно
робимо висновок, що продукція А, С та D
нерентабельна,
бо значення відповідних їм двоїстих
оцінок оптимального плану двоїстої
задачі
 (
).
(
).
Розрахуємо доцільність розширення асортименту за рахунок введення нової продукції.
За умов задачі нам запропоновано включити у виробництво нову продукцію (позначимо цю продукцію Е). Відомі витрати кожного ресурсу на виготовлення одиниці цієї продукції, що становлять 4,5; 6,5; 13 грошових одиниць. Ціна реалізації одиниці продукції дорівнює 55 грош. од.
Складемо відповідне обмеження двоїстої задачі. Позначимо новий вид продукції через , тому маємо:

Y* = (y1=0; y2=0; y3=6,4)
Перевіримо виконання цього обмеження:
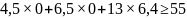

Обмеження виконується як строга нерівність. Це значить, що за умов даного підприємства розширення асортименту за рахунок введення продукції Е буде недоцільним.
Врахування обмежень попиту на продукцію
Введемо два додаткових обмеження попиту на продукцію:
(1)
 (2)
(2)
(3)
Побудуємо до неї модель двоїстої задачі:
(1')
 (2')
(2')
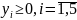 (3')
(3')
Розв’яжемо початкову та двоїсту ЗЛП за допомогою Excel:

