
- •Побудуємо математичну модель початкової задачі
- •Побудуємо математичну модель двоїстої задачі
- •Розв’яжемо початкову злп симплекс-методом:
- •Розв’язання початкової та двоїстої злп в середовищі Excel
- •Дамо економічне тлумачення основним та додатковим змінним початкової та двоїстої задач, а також значення їхніх цільових функцій.
- •Визначимо дефіцитні та недефіцитні ресурси. Розрахуємо межі зміни дефіцитних ресурсів.
- •Визначимо рентабельну та нерентабельну продукцію.
- •Розрахуємо доцільність розширення асортименту за рахунок введення нової продукції.
- •Врахування обмежень попиту на продукцію
Варіант №11
Умова: Підприємство випускає 4 види продукції, використовуючи 3 види ресурсів. Відомі норми витрат ресурсів кожного типу на одиницю продукції, запаси всіх видів ресурсів та ціна одиниці продукції кожного типу.
Завдання: Необхідно визначити оптимальний план виробництва продукції, за якого виручка від її реалізації буде найбільшою та провести економічний аналіз та провести аналіз оптимального плану.
Ресурси |
Норми витрат ресурсів на одиницю продукції |
Запас ресурсів |
Нова продукція |
|||||
A |
B |
C |
D |
|||||
4 |
3 |
4 |
4 |
3800 |
4,5 |
|||
5 |
1 |
7 |
4 |
3500 |
6,5 |
|||
9 |
7 |
11 |
12 |
7000 |
13 |
|||
Ціна од. продукції |
40 |
45 |
47 |
35 |
|
55 |
||
Побудуємо математичну модель початкової задачі
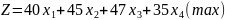 (1)
(1)
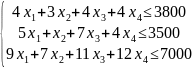 (2)
(2)
 (3)
(3)
Побудуємо математичну модель двоїстої задачі
Упорядкуємо запис вихідної задачі, з поданої умови витікає, що задача упорядкована, тобто:
Число змінних уі двоїстої задачі дорівнює числу співвідношень в системі (2) вихідної задачі. А число співвідношень в системі обмежень двоїстої задачі дорівнює числу змінних хj .
 =>
=>

Запишемо двоїсту задачу до прямої задачі лінійного програмування:
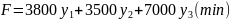 (1')
(1')
 (2')
(2')
 (3')
(3')
Отже, кожна із двоїстих задач є самостійною ЗЛП і може бути розв’язана незалежно одна від іншої.
Розв’яжемо початкову злп симплекс-методом:
Базис |
Сбазис |
|
40 |
45 |
47 |
35 |
0 |
0 |
0 |
Θ |
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
0 |
3800 |
4 |
3 |
4 |
4 |
1 |
0 |
0 |
950 |
|||||||||
|
0 |
3500 |
5 |
1 |
7 |
4 |
0 |
1 |
0 |
500 |
|||||||||
|
0 |
7000 |
9 |
7 |
11 |
12 |
0 |
0 |
1 |
636 |
|||||||||
|
0 |
-40 |
-45 |
-47 |
-35 |
0 |
0 |
0 |
|
||||||||||
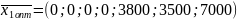
Вводимо
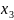
Виводимо
Базис |
Сбазис |
|
40 |
45 |
47 |
35 |
0 |
0 |
0 |
Θ |
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
0 |
1800 |
1,14 |
2,6 |
0 |
1,7 |
1 |
-0,6 |
0 |
700 |
|||||||||
|
47 |
500 |
0,7 |
0 |
1 |
0,6 |
0 |
0,14 |
0 |
3500 |
|||||||||
|
0 |
1500 |
1,14 |
5,4 |
0 |
5,7 |
0 |
-0,3 |
1 |
276 |
|||||||||
|
235000 |
-7 |
-39 |
0 |
-8 |
0 |
7 |
0 |
|
||||||||||
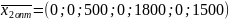
Вводимо
Виводимо
Базис |
Сбазис |
|
40 |
45 |
47 |
35 |
0 |
0 |
0 |
Θ |
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
0 |
1090 |
0,6 |
0 |
0 |
-1 |
1 |
0 ,2 |
-0,5 |
6303 |
|||||||||
|
47 |
461 |
0,7 |
0 |
1 |
0,4 |
0 |
0,2 |
-0,14 |
2500 |
|||||||||
|
45 |
276 |
0,2 |
1 |
0 |
1,05 |
0 |
-0,3 |
0,2 |
- |
|||||||||
|
34087 |
1 |
0 |
0 |
32 |
0 |
-4 |
7 |
|
||||||||||
Вводимо
Виводимо
Базис |
Сбазис |
|
40 |
45 |
47 |
35 |
0 |
0 |
0 |
Θ |
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
0 |
800 |
1 |
0 |
-0,9 |
1,06 |
1 |
0 |
-0,4 |
|
|||||||||
|
0 |
2500 |
3,7 |
0 |
5,4 |
2,3 |
0 |
1 |
-0,14 |
|
|||||||||
|
45 |
1000 |
1,3 |
1 |
1,6 |
0,9 |
0 |
0 |
0,14 |
|
|||||||||
|
45000 |
17,85 |
0 |
23,7 |
42,1 |
0 |
0 |
6,4 |
|
||||||||||
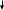
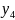
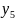
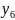
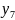
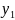
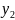

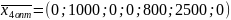

За рядком оцінок останньої симплекс-таблиці знаходимо оптимальний розв’язок двоїстої задачі:
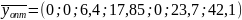
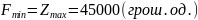

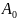


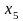
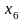

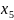

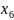

 ,14
,14