§4. Колебательные контуры и их частотные характеристики.

§4.1. Последовательный колебательный контур.

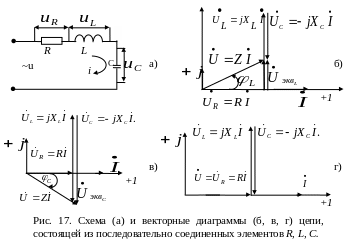
Наиболее общий случай представляет собой цепь переменного тока состоящая из последовательно соединенных участков с активным сопротивлением R , индуктивностью L и емкостью С (рис. 17). Активное сопротивление характеризует активный (необратимый) процесс преобразования электрической энергии в другие виды энергии, а индуктивность и емкость - обратимый процесс преобразования энергии электромагнитного поля. Если по такой цепи пропустить синусоидальный ток , комплексное действующее значение которого то, по второму закону Кирхгофа, в комплексной форме для действующих значений подводимое к цепи напряжение равно сумме напряжений на отдельных участках цепи:

Как известно:

Поэтому

.

Запишем закон Ома в комплексной форме: ,

где Z - комплексное полное сопротивление

где 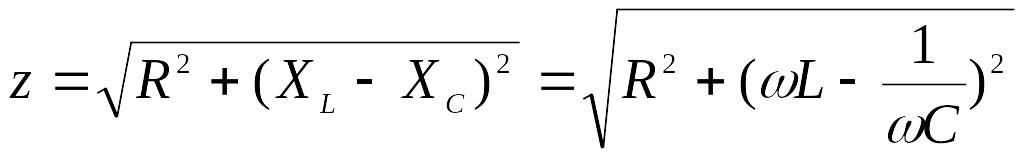- модуль полного сопротивления.

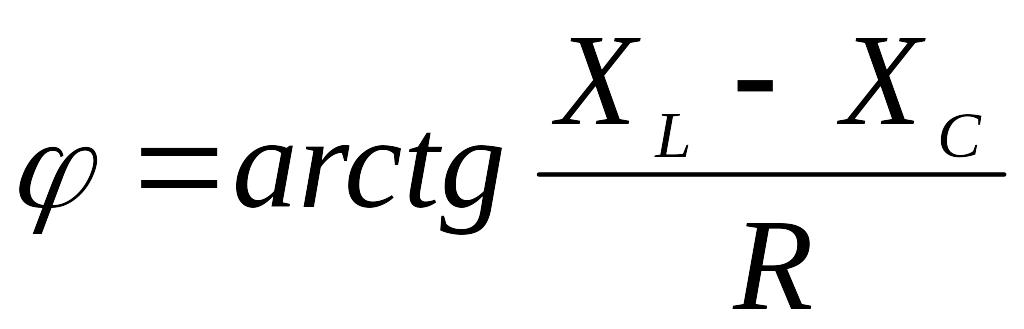- его аргумент.

Для упрощения записи комплексных полных сопротивлений вводят понятие реактивного сопротивления двухполюсника X. Оно является алгебраической разностью индуктивного и емкостного сопротивлений:

Комплексная полная мощность рассматриваемого двухполюсника:

Знак угла сдвига фаз определяется знаком реактивного сопротивления X. В зависимости от соотношения между индуктивным и емкостным сопротивлениями двухполюсник может быть: индуктивным (при X_L>X_C), емкостным (при X_L<X_C ), чисто активным (при X_L=X_C).

1. Индуктивный двухполюсник: X_L>X_C. Комплексное полное сопротивление:

Реактивное сопротивление такого двухполюсника носит индуктивный характер (эквивалентное индуктивное сопротивление). Для данного случая построена векторная диаграмма (рис. 17,б). Подводимое напряжение U опережает ток цепи на угол сдвига фаз φ_L.

2. Емкостный двухполюсник: X_L<X_C. Комплексное полное сопротивление:

Эквивалентное реактивное сопротивление такого двухполюсника носит емкостный характер . Для указанного случая векторная диаграмма приведена на рис. 17, в. Подводимое напряжение U отстает от тока цепи на угол сдвига фаз φ_С.

3. Активный двухполюсник: X_L=X_C. Комплексное полное сопротивление этой цепи чисто активное: Z=R.

Эквивалентное реактивное сопротивление такого двухполюсника равно нулю. На рис. 17, г представлена векторная диаграмма для данного случая. Подводимое напряжение U совпадает по фазе с током: φ=0.

Явление, при котором в последовательной цепи из элементов R, L и С подводимое напряжение цепи совпадает по фазе с её током, называется резонансом напряжений.

§4.2. Резонанс напряжения.

Основным условием возникновения резонанса напряжений в последовательном контуре является равенство реактивных сопротивлений X_L=X_C. В этом случае угол сдвига фаз между током и напряжением равен нулю (φ=0) и полное сопротивление цепи равно ее активному сопротивлению.

Из равенства реактивных сопротивлений X_L=X_C или 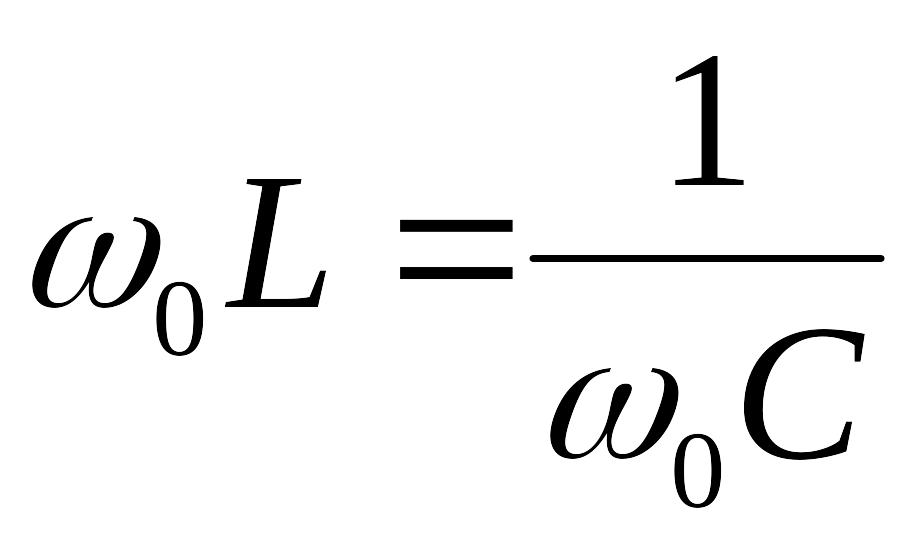следует, что резонанс можно достичь, изменяя или частоту подводимого напряжения, или параметры контура - индуктивность L или емкость C. Частота, при которой наступает резонанс, называется собственной угловой частотой

Индуктивное и емкостное сопротивление при резонансе равны:

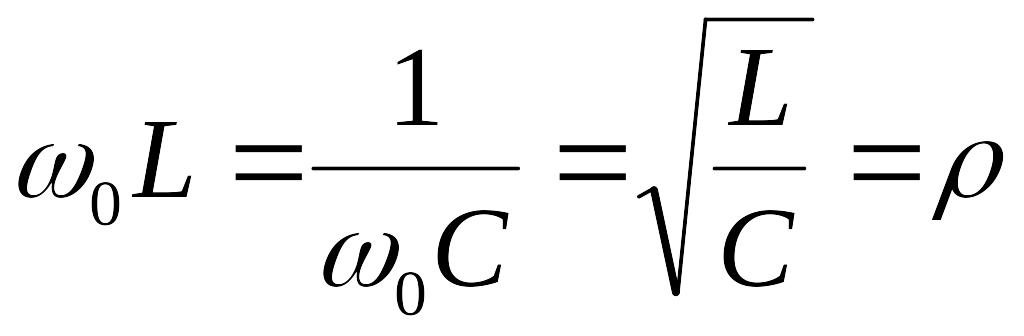(1)

Величина ρ называется волновым или характеристическим сопротивлением цепи.

При резонансе напряжений полное сопротивление цепи равно активному сопротивлению и минимально, а ток такой цепи

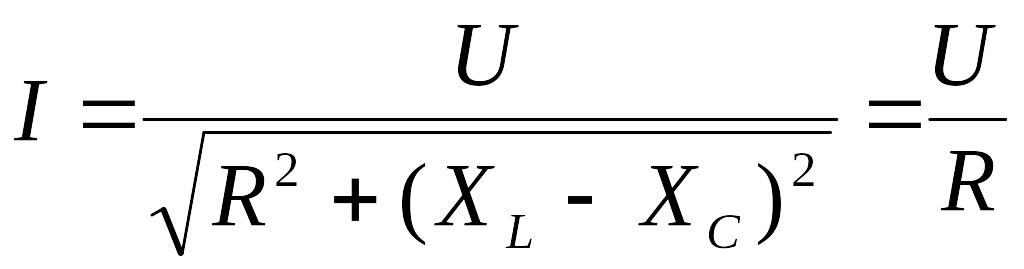- максимален.

Умножив уравнение (1) на ток, получим, что при резонансе напряжения на индуктивности и емкости равны:

(2)

Если активное сопротивление цепи R невелико ( ), то при резонансе сила тока в цепи резко возрастает, и одновременно сильно возрастают напряжения на емкости и индуктивности. Они во много раз могут превысить напряжение на входных зажимах цепи. Это свойство является важнейшей особенностью резонанса напряжений и широко используется в технике. Найдем отношение напряжений на реактивных элементах к подводимому:

, (3)

где 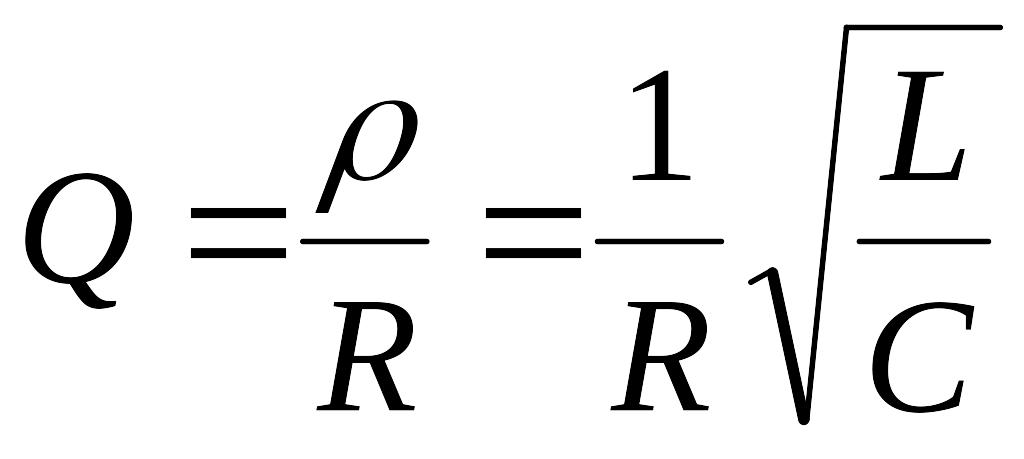- добротность цепи.

Физическая причина возникновения повышенных частичных напряжений - это колебания значительных количеств энергии между электрическим полем емкости и магнитным полем индуктивности. Умножив равенство (2) на ток получим равенство реактивных индуктивной и емкостной мощностей:

Энергия, поступающая от источника

затрачивается на потери в активном сопротивлении, достаточна для того, чтобы в системе поддерживались колебания энергии между магнитным и электрическими полями. Суммарная энергия электрического и магнитного поля при этом остается постоянной:

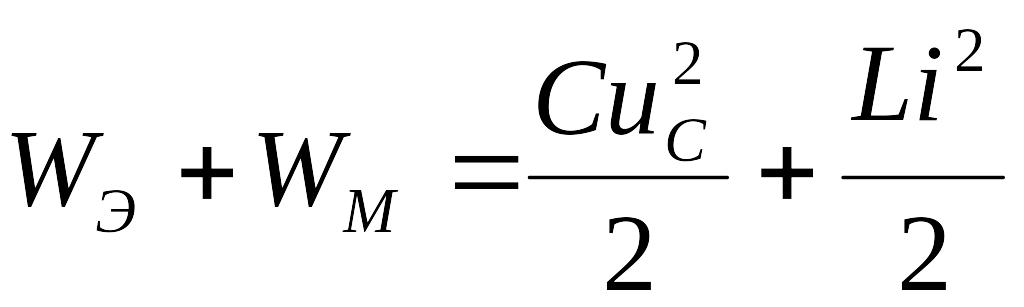(4)

Как известно, если , то . Подставив эти выражения в уравнение (4), получим:

Амплитуда тока , a 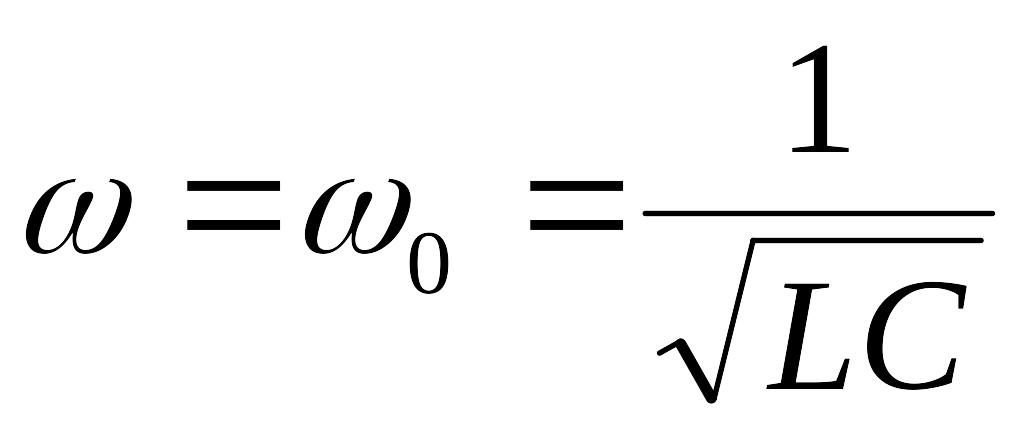, следовательно, , на основании чего

Для техники связи, автоматики, радиоэлектроники и т.д. большое практическое значение имеет зависимость параметров цепи от частоты, которая называется амплитудно-частотной характеристикой контура. Зависимость действующих значений токов и напряжений цепи от частоты называется резонансными характеристиками.

Активное сопротивление большинства устройств от частоты не зависит. Зависимости индуктивного X_L и емкостного X_C сопротивлений от частоты определяются формулами . Они изображены на рис. 18, а. Реактивное сопротивление цепи При , X_L< X_C, X носит ёмкостный характер. При наступает резонанс напряжений (X_L=X_C) сопротивление цепи чисто активное. При , X_L>X_C и реактивное сопротивление носит индуктивный характер.

Резонансные характеристики представлены на рис. 18, б. При наличии в цепи сопротивления R наибольшие значения напряжений на реактивных элементах будут на частотах, отличных от резонансной частоты.

Н апряжение на емкости равно:

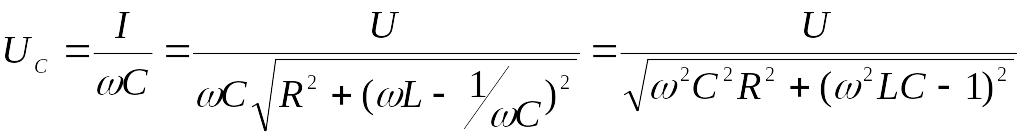(5)

Наибольшему значению U_c как функции ω соответствует минимум подкоренного выражения в формуле (5). Следовательно, чтобы определить условия максимума U_с(ω), нужно приравнять нулю первую производную по ω от этого выражения:

На основании этого искомая угловая частота:

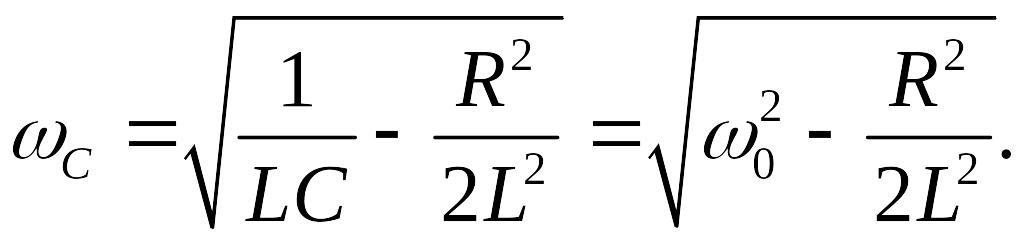
Следовательно, напряжение на ёмкости U_c будет иметь наибольшее значение при ω_c<ω₀ .

Поступая аналогичным образом, найдем, что частота, при которой напряжение U_L достигнет максимума, равна:

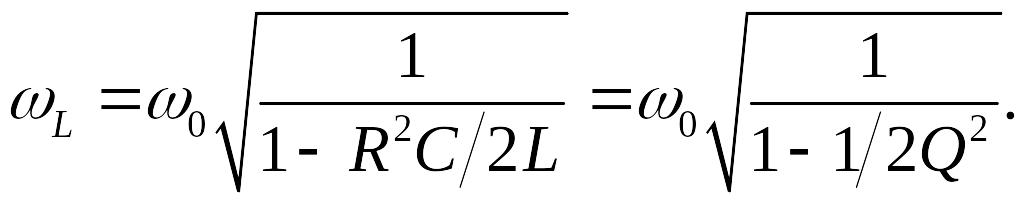
Следовательно: напряжение на индуктивности U_L будет иметь наибольшее значение при ω_L>ω₀.

Чем больше добротность схемы 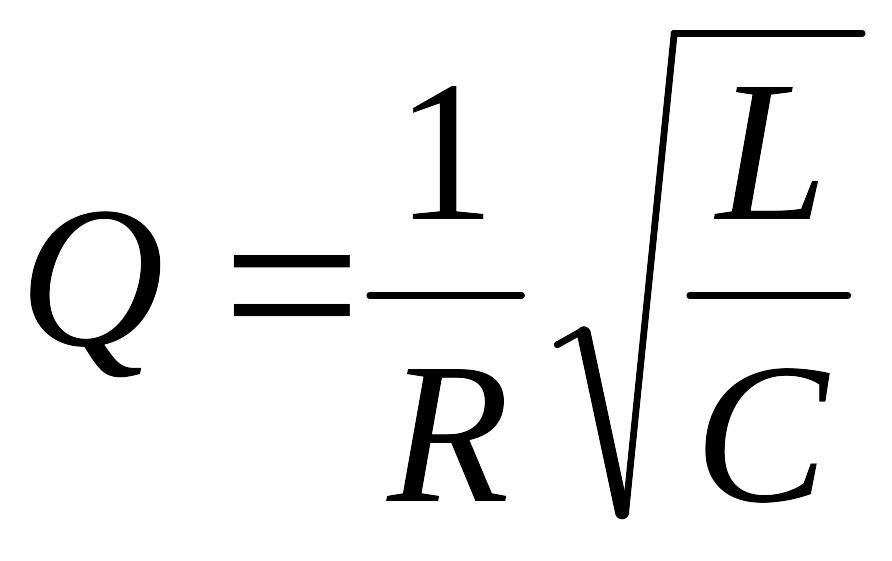, тем ближе вершины характеристик U_C , U_L(ω) и тем острее эти характеристики.

Из уравнения (3) следует, что: . Таким образом, при резонансе напряжения на индуктивности и емкости в последовательном колебательном контуре резко возрастают, поэтому этот резонанс называется резонансом напряжений. Резкое увеличение напряжение на конденсаторе при резонансе позволяет использовать последовательный колебательный контур в качестве частотно-избирательной системы для выделения из множества сигналов только одного, несущая частота которая совпадает с частотой собственных колебаний в контуре.

График зависимости тока от частоты (рис. 18б) показывает, что рассматриваемая цепь обладает избирательными свойствами. Цепь обладает наименьшим сопротивлением для тока той частоты, которая наиболее близка к ее резонансной частоте.