§3.5. Расчет активно-емкостной цепи, треугольники напряжений, сопротивлений; мощность.

Рассмотрим электрическую цепь, состоящую из источника питания, активного сопротивления и емкости, включенных последовательно. Эквивалентная схема такого двухполюсника приведена на рис. 15а.

Пусть по данной цепи проходит ток:

(1)

По второму закону Кирхгофа подводимое к этому двухполюснику напряжение равно сумме напряжений на отдельных участках цепи. В комплексной форме для действующих значений напряжений можно записать:

(2)

Учитывая значения комплексных напряжений и , получим комплексное действующее значение напряжения на входе

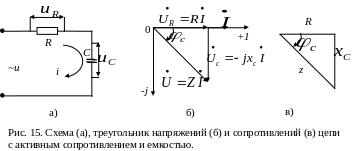(3)

Из уравнения (3) можно записать формулу закона Ома в комплексной форме:

(4)

Z – комплексное полное сопротивление:

(5)

где - модуль полного сопротивления, (6)

- его аргумент.

Подставим в формулу (3) значение Z и , получим:

(7)

Из (7) определим модуль напряжения и его начальную фазу:

, (8)

Начальная фаза напряжения меньше начальной фазы тока на угол сдвига фаз . Следовательно, напряжение на входе емкостного двухполюсника отстает по фазе от тока на угол сдвига фаз .

На рис. 15б приведена векторная диаграмма емкостного двухполюсника. Для упрощения принято , тогда вектор тока совпадет с осью +1. Активное падение напряжения совпадает по фазе с током, а вектор емкостного напряжения отстает от тока на . Вектор подводимого напряжения равен геометрической сумме векторов: . Он отстает от тока на угол сдвига фаз . Если каждую из сторон треугольника напряжений разделить на ток , то получим треугольник сопротивлений (рис. 15в). Из него можно определить угол сдвига фаз по формуле:

(9)

Определим мгновенную мощность емкостного двухполюсника, полагая начальную фазу тока равной нулю:

(10)

Среднее значение мощности:

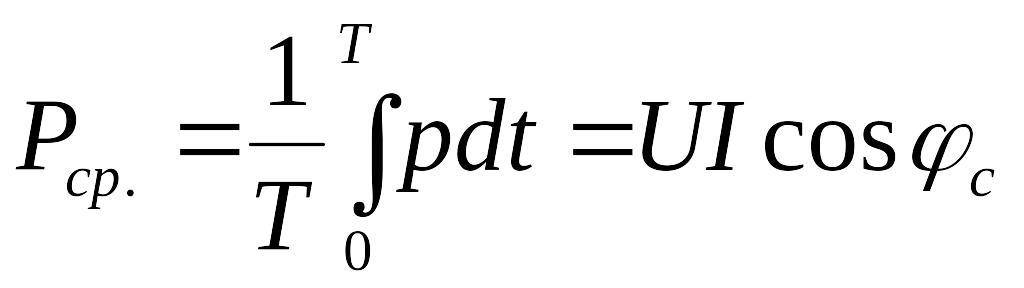(11)

Учитывая, что , , то

(12)

Как и для индуктивного двухполюсника, среднее значение мощности емкостного двухполюсника равно его активной мощности.

Реактивная мощность характеризует амплитуду колебаний мощности обмена энергией между электрическим полем конденсатора и цепью:

(13)

Полная мощность

(14)

Комплексная полная мощность

(15)

И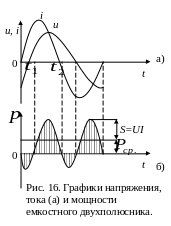 з уравнения (15) следует, что реактивная емкостная мощность является отрицательной.

На рис. 16 построены графики мгновенных значений напряжения, тока (а) и мощности (б). Из графиков видно, что в промежутке времени , когда мощность положительна , происходит одновременное преобразование энергии, поступающей от источника питания, в тепловую энергию и в энергию электрического поля .

В промежутки времени , когда мощность отрицательна , энергия частично возвращается обратно к источнику. В момент к источнику возвращается энергия, равная заштрихованной площадке, ограниченной участком кривой и осью абсцисс.