
- •Глава 1. Основные теории электрических цепей и сигналов.
- •§1. Основные понятия теории электрических цепей.
- •§ 2. Элементы электрических цепей и их уравнения. Классификация цепей по признаку линейности.
- •§ 3. Зависимые (управляемые) источники.
- •§ 4.Топологические параметры. Электрическая цепь и уравнение соединений.
- •Глава 2. Электрические цепи при гармоническом воздействии.
- •§1. Основные понятия линейных цепей. Среднее и действующее значение синусоидального тока.
- •§2. Гармонические колебания. Изображение синусоидальных токов векторами и комплексными числами.
- •§3. Комплексная форма уравнений элементов.
- •§3.1. Цепь переменного тока с резистором, активная мощность.
- •§3.2. Цепь переменного тока с индуктивностью, реактивная мощность.
- •§3.3. Цепь переменного тока с емкостью.
- •§3.4. Расчет цепи с реальной индуктивностью.
- •§3.5. Расчет активно-емкостной цепи, треугольники напряжений, сопротивлений; мощность.
- •§4. Колебательные контуры и их частотные характеристики.
- •§4.1. Последовательный колебательный контур.
- •§4.2. Резонанс напряжения.
- •§4.3. Свободные колебания в реальном lc - контуре.
- •§4.4. Уравнение резонансной кривой последовательного контура.
- •§4.5. Вынужденные колебания в параллельном колебательном контуре. Резонанс токов.
- •§4.6. Связанные контуры как полосовой фильтр.
- •Глава 5. Электронные приборы.
- •§1. Классификация электронных приборов.
- •В газоразрядных (или ионных) приборах движение электронов происходит в атмосфере инертных газов. Электрические процессы в них представляют собой разряд в газе.
- •§2. Полупроводниковые приборы.
- •§2.1. Собственная электропроводность.
- •§2.2. Примесные полупроводники.
- •§2.3. Электронно-дырочный переход.
- •§3. Полупроводниковые диоды, их свойства и назначение.
- •§3.1. Применение полупроводниковых диодов для выпрямления переменного тока.
- •§3.2. Полупроводниковые стабилитроны.
- •§3.3. Варикапы.
- •§3.4. Тиристор.
- •§3.5. Оптоэлектронные устройства.
- •§3.6. Фотодиоды.
- •§4. Полевые транзисторы.
- •§4.1. Полевой транзистор с управляющим p-n-переходом.
- •§4.2. Полевые транзисторы с изолированным затвором.
- •§4.3. Дифференциальные параметры полевых транзисторов.
- •§ 5. Биполярные транзисторы.
- •§ 5.1. Статические характеристики. Дифференциальные параметры транзистора.
- •§ 5.2. Определение н-параметров транзисторов по характеристикам.
- •Глава 6. Усилители.
- •§1. Основные показатели.
- •§2. Резисторный усилитель напряжения.
- •Из последней формулы следует, что для расширения полосы пропускания усилителя в сторону верхних частот необходимо уменьшать с0Rэ.
- •§3. Дифференциальный усилитель.
- •§4. Операционные усилители.
- •§5. Основные схемы включения операционных усилителей.
- •§6. Обратная связь в усилительных устройствах.
- •Коэффициент передачи усилителя с обратной связью:
- •§7. Диаграмма Найквиста
- •§8. Повышение стабильности усиления и расширение полосы
- •§9. Частотно-зависимая обратная связь
- •При малых относительных расстройках .
§3. Комплексная форма уравнений элементов.
§3.1. Цепь переменного тока с резистором, активная мощность.
Пусть на вход цепи с известным активным сопротивлением (рис. 5) приложено синусоидальное напряжение
![]() (1)
(1)
Необходимо установить, как будут изменятся ток и мощность цепи.
По закону Ома для мгновенных значений ток цепи:
![]() (2)
(2)
И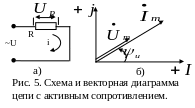 з
сопоставления уравнений (1) и (2) следует,
что сдвиг фаз
з
сопоставления уравнений (1) и (2) следует,
что сдвиг фаз
![]() ,
т. е. ток и напряжение совпадают по фазе
и векторная диаграмма имеет вид,
представленный на рис. 5. Комплексная
амплитуда тока
,
т. е. ток и напряжение совпадают по фазе
и векторная диаграмма имеет вид,
представленный на рис. 5. Комплексная
амплитуда тока
![]() .
.
Разделив левую и правую части этого
равенства на
![]() ,
получим соотношение для действующих
значений токов и напряжений:
,
получим соотношение для действующих
значений токов и напряжений:
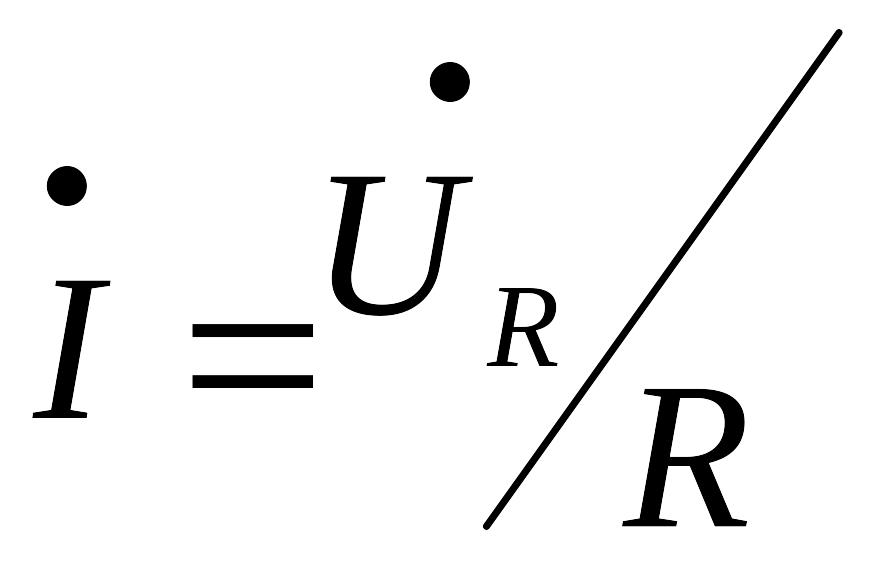 (3)
(3)
Уравнение (3) выражает закон Ома в комплексной форме для участка цепи с активным сопротивлением.
Мгновенная мощность электрической цепи с активным сопротивлением равна произведению мгновенных значений напряжения и тока:
![]() (4)
(4)
Среднее значение мощности за период:
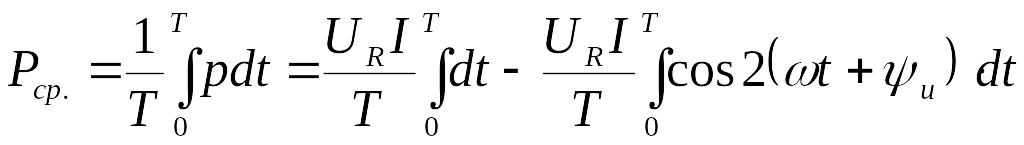
или
![]() (5)
(5)
Если в выражение (5) подставить значение
![]() ,
тогда получим, что среднее значение
мощности
,
тогда получим, что среднее значение
мощности
![]() ,
которая преобразуется в активном
сопротивлении в тепловую энергию равно:
,
которая преобразуется в активном
сопротивлении в тепловую энергию равно:
![]()
Графики изменения напряжения, тока и
мощности цепи с активным сопротивлением,
представлены на рис. 6 для случая, когда
начальная фаза
![]() .
Из графиков видно, что мгновенная
мощность изменяется от нуля до
.
Из графиков видно, что мгновенная
мощность изменяется от нуля до
![]() ,
оставаясь все время положительной. Это
означает, что при любом направлении
тока поступающая из сети энергия
превращается в тепловую энергию и,
нагревая резистор R,
рассеивается в окружающее пространство.
,
оставаясь все время положительной. Это
означает, что при любом направлении
тока поступающая из сети энергия
превращается в тепловую энергию и,
нагревая резистор R,
рассеивается в окружающее пространство.
З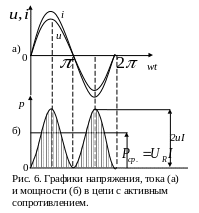 аштрихованная
на рисунке площадь равна преобразованной
в теплоту энергии.
аштрихованная
на рисунке площадь равна преобразованной
в теплоту энергии.
§3.2. Цепь переменного тока с индуктивностью, реактивная мощность.
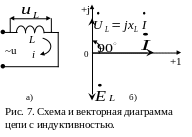 Обмотки
электрических машин и аппаратов, а также
индуктивные катушки, используемые в
различных устройствах радиоэлектроники,
характеризуются параметром индуктивность
L. Любая катушка наряду
с индуктивностью L
обладает также активным сопротивлением
R. Рассмотрим катушку
с индуктивностью L,
активным сопротивлением которой можно
пренебречь, т. е. идеальную катушку
(рис. 7а). Пусть ток в цепи изменяется по
гармоническому закону
Обмотки
электрических машин и аппаратов, а также
индуктивные катушки, используемые в
различных устройствах радиоэлектроники,
характеризуются параметром индуктивность
L. Любая катушка наряду
с индуктивностью L
обладает также активным сопротивлением
R. Рассмотрим катушку
с индуктивностью L,
активным сопротивлением которой можно
пренебречь, т. е. идеальную катушку
(рис. 7а). Пусть ток в цепи изменяется по
гармоническому закону
![]() (1)
(1)
Этот ток создает в катушке синусоидально изменяющийся поток, который наводит в ней э. д. с. самоиндукции
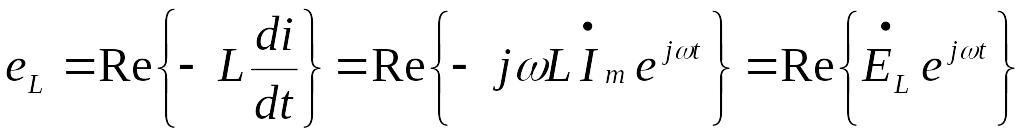 ,
,
где
![]() ,
(2)
,
(2)
![]() (3)
(3)
Действующие значение э.д.с.
самоиндукции равно
![]() .
Из формулы (3) следует, что э.д.с. самоиндукции
отстает по фазе от тока на угол
.
Из формулы (3) следует, что э.д.с. самоиндукции
отстает по фазе от тока на угол
![]() .
.
Напряжение источника
![]() должно компенсировать э. д. с. самоиндукции
должно компенсировать э. д. с. самоиндукции
![]() и изменяться по закону:
и изменяться по закону:
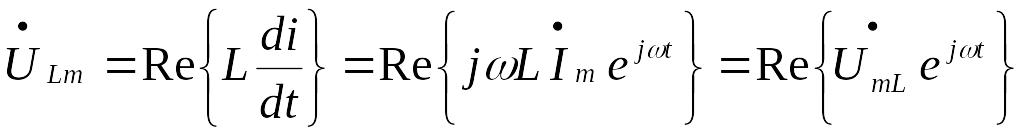 .
(4)
.
(4)
Комплексная амплитуда напряжения на индуктивности:
![]() (5)
(5)
![]() ,
напряжение на индуктивности опережает
по фазе ток на угол
,
напряжение на индуктивности опережает
по фазе ток на угол
![]() .
Разделив правые и левые части этих
выражений на
,
получим комплексные действующие значения
тока и напряжения на индуктивности:
.
Разделив правые и левые части этих
выражений на
,
получим комплексные действующие значения
тока и напряжения на индуктивности:
,
|
(6) |
Графики напряжения, тока и
мощности цепи с идеальной индуктивностью,
представлены на рис. 8 для случая, когда
начальная фаза
![]() .
.
Произведение
![]() имеет размерность сопротивления. Его
обозначают буквой
имеет размерность сопротивления. Его
обозначают буквой
![]() и называют реактивным индуктивным
сопротивлением:
и называют реактивным индуктивным
сопротивлением:
![]() (7)
(7)
Э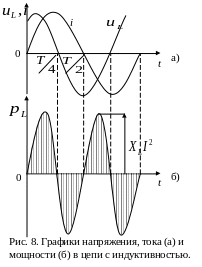 то
сопротивление учитывает реакцию
электрической цепи на изменение
магнитного потока в индуктивности.
Индуктивное сопротивление прямо
пропорционально индуктивности катушки
и частоте проходящего по ней тока,
зависимость
то
сопротивление учитывает реакцию
электрической цепи на изменение
магнитного потока в индуктивности.
Индуктивное сопротивление прямо
пропорционально индуктивности катушки
и частоте проходящего по ней тока,
зависимость
![]() от частоты
от частоты
![]() ,
называется частотной характеристикой
индуктивности, представлена на рис. 9.
,
называется частотной характеристикой
индуктивности, представлена на рис. 9.
Из уравнения (6) можно получить закон Ома в комплексной форме для цепи с индуктивностью:
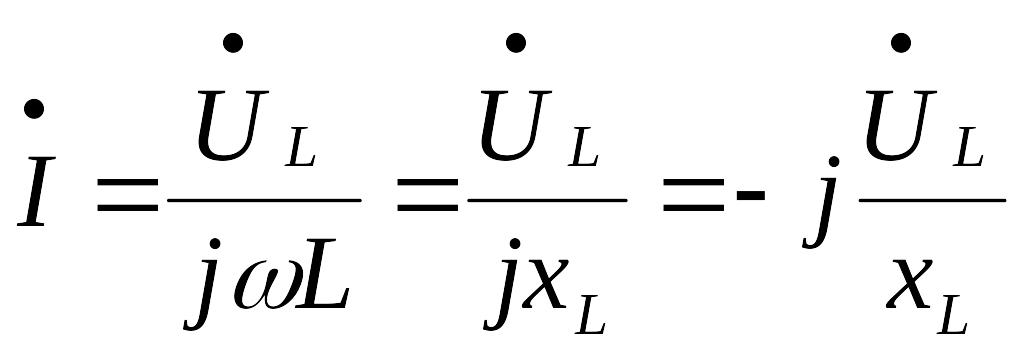 (8)
(8)
Мгновенная мощность в цепи с индуктивностью определяется формулой:
![]()
![]() (9)
(9)
Отсюда следует, что мгновенная
мощность в цепи с индуктивностью
изменяется с частотой в два раза большей,
чем частота тока (рис. 8б). В первую
четверть периода, когда ток и напряжение
положительны, мощность также положительна.
Энергия от источника переходит в
индуктивный элем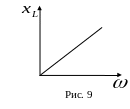 ент,
где она затрачивается на создание
магнитного поля. К концу первой четверти
периода поле имеет максимальную энергию
ент,
где она затрачивается на создание
магнитного поля. К концу первой четверти
периода поле имеет максимальную энергию
![]() ,
равную заштрихованной площади, во
вторую четверть периода ток убывает,
но остается положительным. Напряжение
,
равную заштрихованной площади, во
вторую четверть периода ток убывает,
но остается положительным. Напряжение
![]() и мощность
и мощность
![]() отрицательны. К концу второй четверти
периода весь запас энергии магнитного
поля
отрицательны. К концу второй четверти
периода весь запас энергии магнитного
поля
![]() возвращается обратно в цепь. Среднее
значение мощности в такой цепи за период
равно нулю:
возвращается обратно в цепь. Среднее
значение мощности в такой цепи за период
равно нулю:
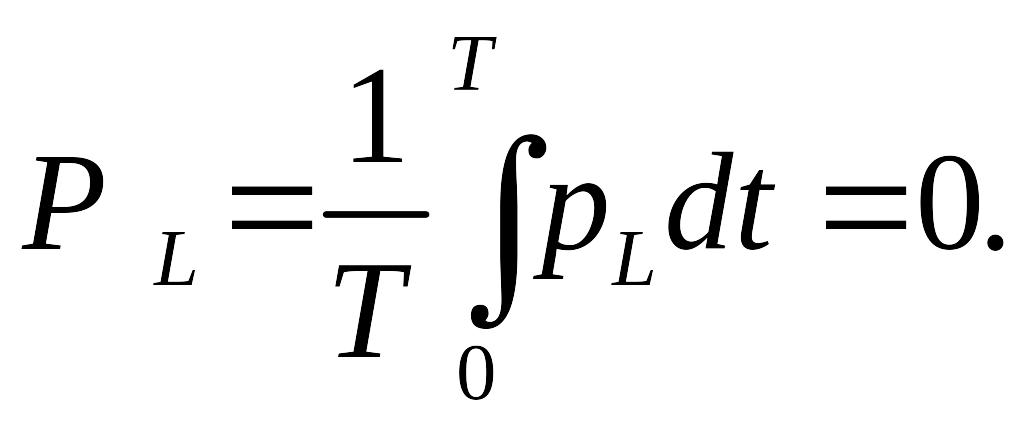
Таким образом, в течение
одного периода электроэнергия дважды
поступает от источника в катушку и
обратно. При этом вся передаваемая
энергия запасается в магнитном поле
катушки и затем вся возвращается
источнику. Такая энергия обмена между
источником и нагрузкой, которая не
преобразуется в другие виды энергии,
называется реактивной мощностью
![]() .
Реактивная мощность равна амплитуде
мгновенной мощности (9), т. е.
.
Реактивная мощность равна амплитуде
мгновенной мощности (9), т. е.
![]() .
.
Реактивная мощность имеет ту же размерность, что и активная мощность. Но для удобства для единиц измерения реактивной мощности принято другое наименование: Вольт-Ампер реактивный (ВАр).
Напряжение на элементе с
индуктивностью
![]() ,
поэтому реактивную мощность можно также
определить по формулам:
,
поэтому реактивную мощность можно также
определить по формулам:
![]() (10)
(10)
где
![]() -
индуктивная проводимость.
-
индуктивная проводимость.
