§4.4. Уравнение резонансной кривой последовательного контура.

В большинстве случаев э.д.с., воздействующая на колебательный контур, является несинусоидальной, содержащей несколько гармонических составляющих. Колебательный контур может быть настроен на частоту одной из них, но расстроен относительно других гармонических составляющих. Найдем соотношение между амплитудами тока какой-либо частоты ω и резонансной частоты ω₀ контура.

Разность между этими частотами

Δω = ω - ω₀ (или Δf = f – f₀) (1)

называется абсолютной расстройкой контура.

Будем рассматривать только такие расстройки, которые удовлетворяют соотношению: Δω<<ω₀.

Реактивное сопротивление расстроенного контура:

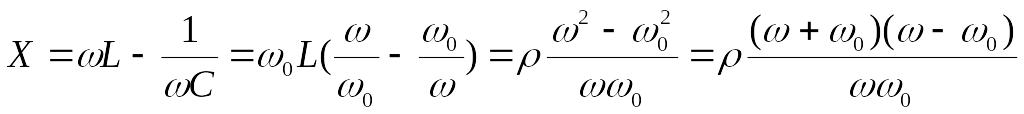(2)

Величина, определяемая отношением

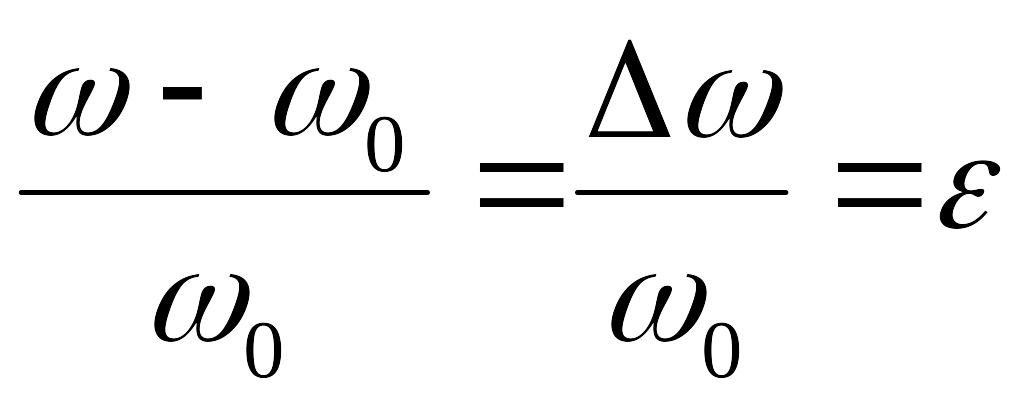, (3)

называется относительной расстройкой контура. Ток в контуре на любой частоте

.

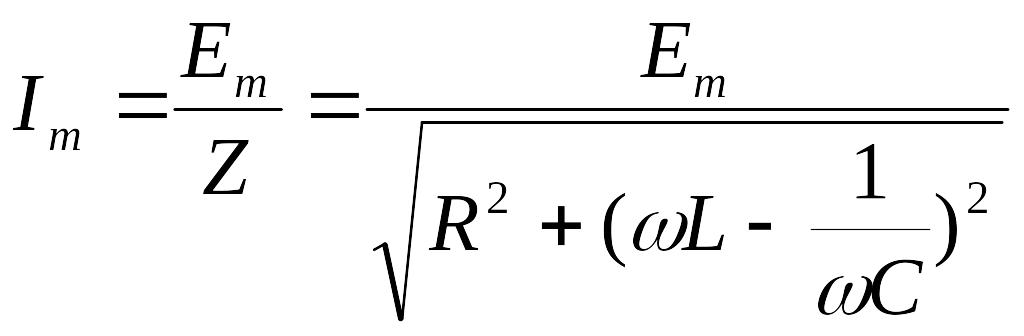При резонансе , и ток . Тогда

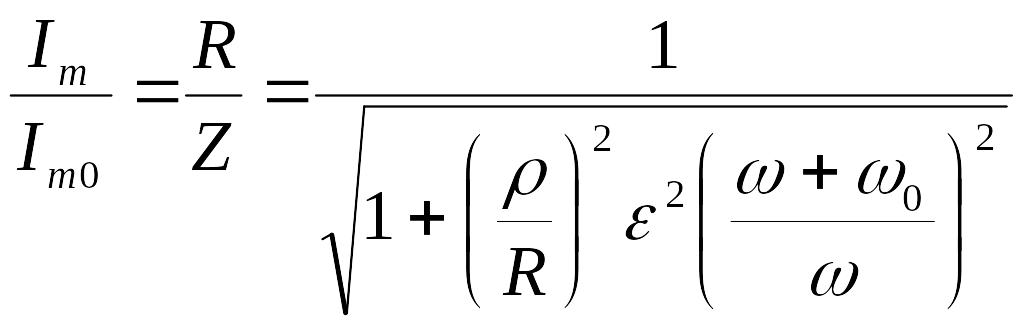(4)

Мы получили уравнение резонансной кривой (4) колебательного контура.

В близи резонанса и и уравнение резонансной кривой вблизи резонанса имеет вид:

(5)

Уравнение (4) справедливо для вершины резонансной кривой (рис. 19) или амплитудно-частотной характеристики последовательного колебательного контура. Острота резонансной характеристики контура определяется его добротностью. Чем выше добротность, тем более резко выражены резонансные свойства контура.

Среди э.д.с. одинаковых амплитуд, но различных частот, наибольший ток в контуре создает та, для которой величина расстройки наименьшая. Из всех э.д.с., воздействующих на контур, последний «избирает» те, частоты которых близки к резонансной. Это свойство контура называется частотной избирательностью, позволяет использовать его в качестве фильтра.

И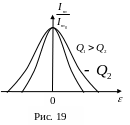 збирательные свойства контура определяет его резонансной характеристикой (рис.19). Необходимо установить, для какой ординаты производить отчет на границе полосы пропускания фильтра. Для неискаженного воспроизведения сигнала коэффициент передачи 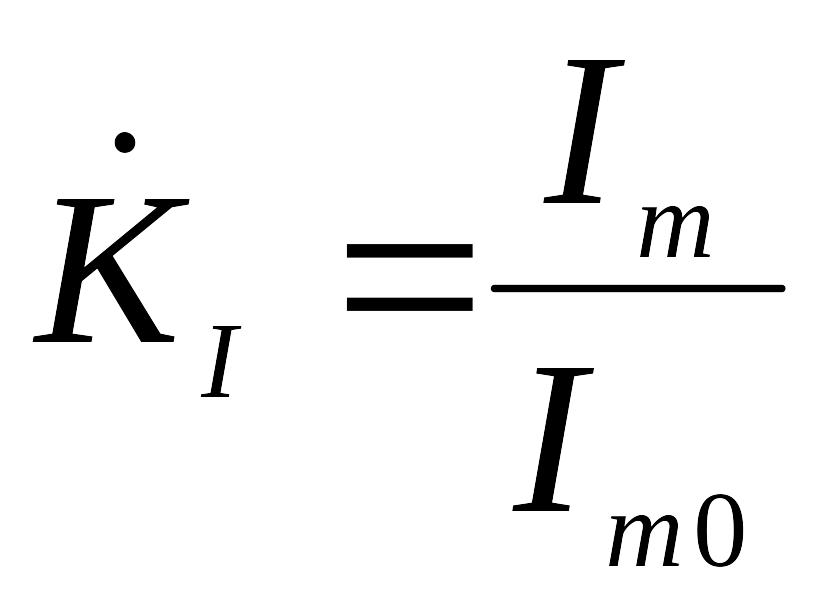должен быть одинаковым для всех передаваемых частот ( ), а аргумент представлять собой линейную функцию частот . - сдвиг фаз между выходным и входным напряжениями. Эта зависимость представлена на рис. 20. Идеальный контур должен иметь П-образную частотную характеристику, а фазо-частотная характеристика должна быть линейной.

АЧХ реального контура отличаются от П-образной. Это приводит к искажению сигнала тем большему, чем сильнее это отличие. Допустимые искажения сигнала зависят от конкретной системы передачи сигнала. В электронике принято считать контур линейным четырехполюсником в рабочей полосе частоты, в которой меняется менее чем в раз.

,

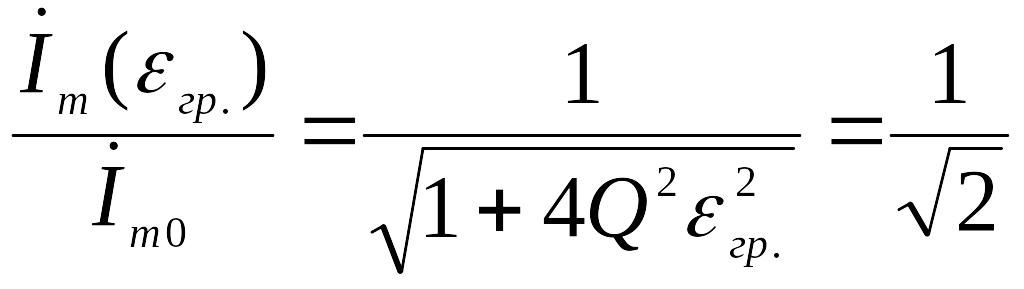где - расстройка, соответствующая граничным частотам фильтра. Тогда относительная полоса пропускания

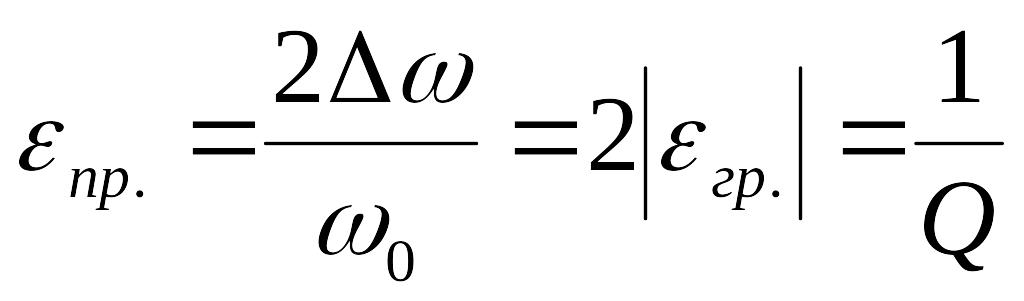
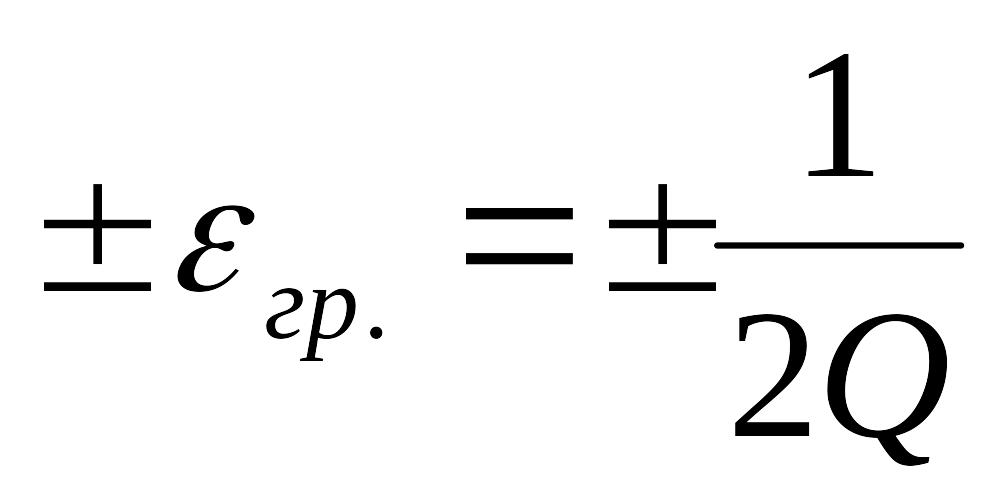(рис. 20)

Абсолютная полоса пропускания равна

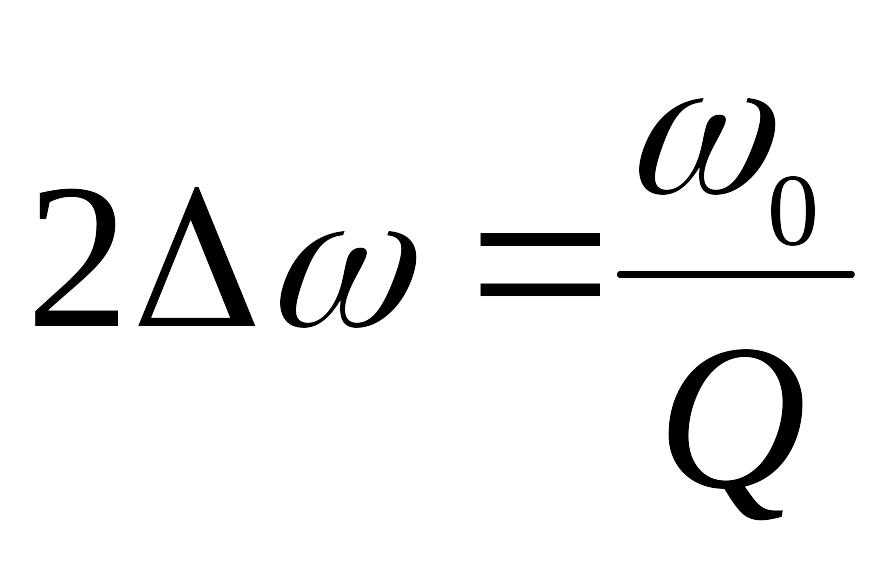или .

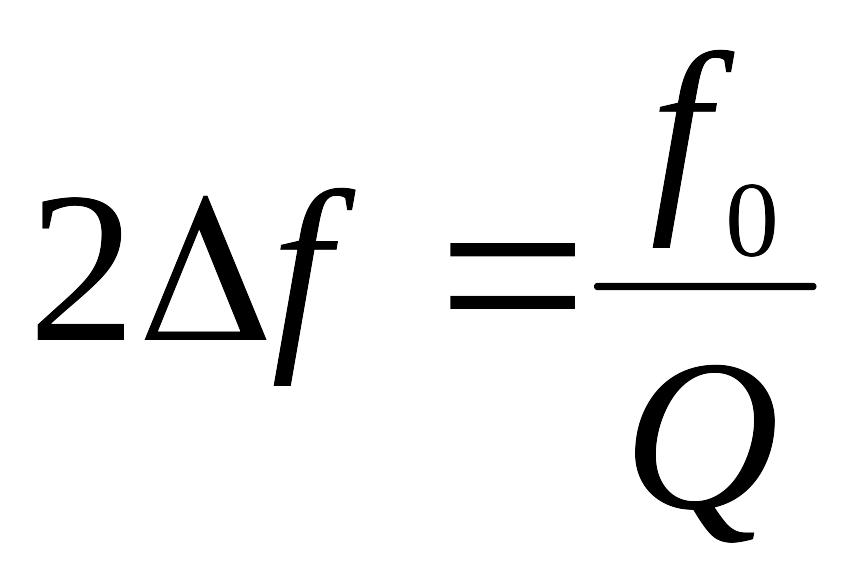Наклон графика (рис. 20) всегда отрицателен, что отражает запоздание по фазе выходного сигнала относительно входного.