1.5.4.3. Кільцевий хвилевідний міст

К

Рис. 1.147

а)

б)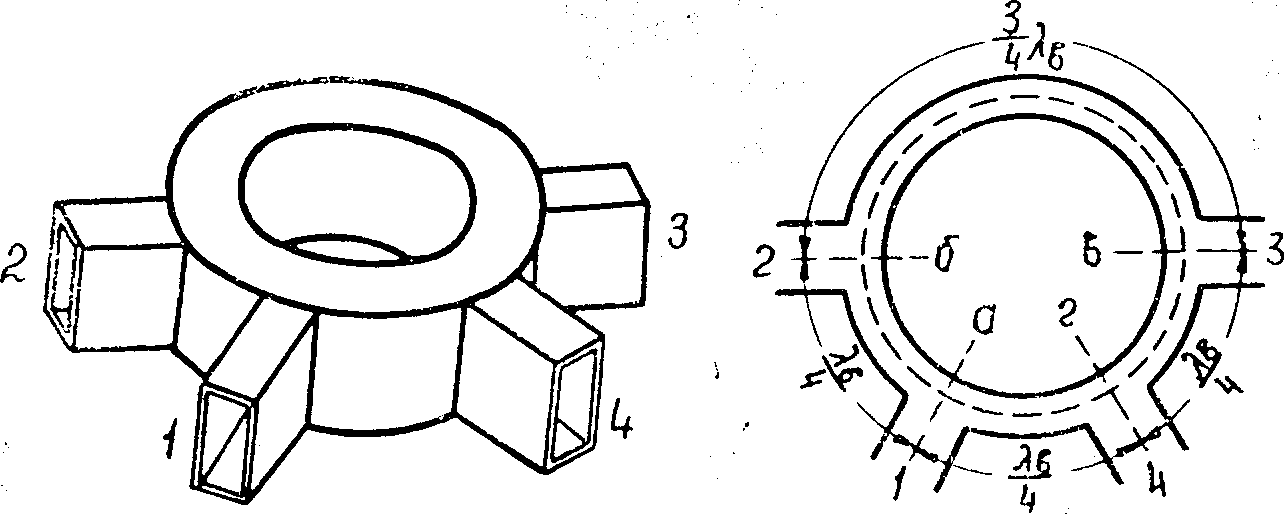

ільцевий хвилевідний міст (рис. 1.147) являє собою прямокутний хвилевід, згорнутий у кільце в площині Е. Довжина хвилеводу по осьовій лінії становить l_х. До широкої стінки хвилевідного кільця підключені чотири відгалуження, які є відрізками прямокутних хвилеводів. Таким чином, цей міст можна представити

Рис. 1.148

у вигляді послідовного з'єднання чотирьох хвилевідних Е-трійників. Схему заміщення кільцевого моста подано на рис. 1.148. Її складено на основі схеми заміщення Е-трійника, який збуджує бічні плечі в протифазі (див. рис. 1.94). Це показано на рис. 1.148 протифазними векторами Е полів, які поширюються від плеча 1 по кільцю. Хвильовий опір кільцевої лінії дорівнює Z, підключені лінії мають хвильові опори Z₀.

Схематично кільцевий міст зображений на рис. 1.147.б. Відстані між відгалуженнями підібрані так, щоб енергія, що надходить із боку будь-якого плеча, ділилася нарівно між сусідніми плечима й не надходила в протилежне плече.

Відомо, що при збудженні трійника з боку плеча Е в плечах основного хвилеводу збуджуються протифазні хвилі однакової амплітуди (рис. 1.102.а). Тому, якщо збуджувати кільцевий міст через одне із плечей, у будь-якому перетині кільцевого хвилеводу поле являє собою суперпозицію двох хвиль. Розглянемо розподіл енергії в кільцевому мосту для різних варіантів живлення за допомогою векторних діаграм. Введемо позначення: — вектор електричного поля хвилі, що поширюється в кільцевому хвилеводі по годинниковій стрілці; — вектор електричного поля хвилі, що поширюється проти годинникової стрілки.

Н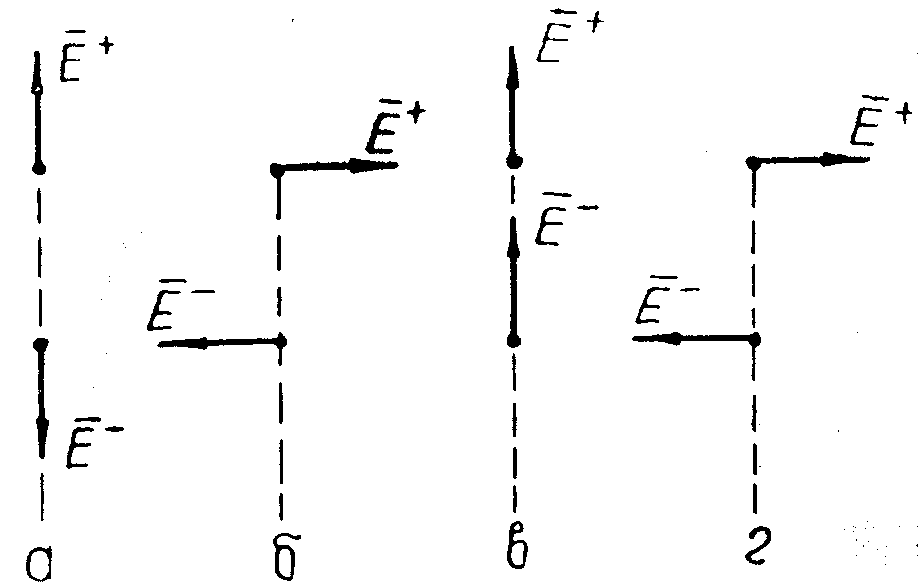 а рис. 1.149 показане розташування векторів, що характеризують фази хвиль у різних перетинах кільцевого хвилеводу при збудженні моста через плече 1. З діаграми видно, що в перетин в хвилі приходять у фазі, тому, отже, у плече 3 (рис. 1.147) кільцевого моста енергія відгалужуватися не буде.

У перетини б и г хвилі приходять у противофазі, отже, виконується умова відгалуження енергії в плечі 2 і 4 кільцевого мосту. З векторної діаграми видно, що коливання в перетинах б і г перебувають у фазі, тому плечі 2 і 4 мосту збуджуються синфазно.

Рис. 1.149 На підставі теореми взаємності можна стверджувати, що при живленні кільцевого моста одночасно з боку плечей 2 й 4 синфазними хвилями рівної амплітуди буде збуджуватися плече 1, а в плече 3 енергія не піде. Ці властивості аналогічні першій і другій властивостям подвійного трійника.

Розташування векторів, що характеризують фази хвиль в перетинах кільця при живленні моста з боку плеча 3, показане на рис. 1.150. З діаграми видно, що енергія відгалужується в п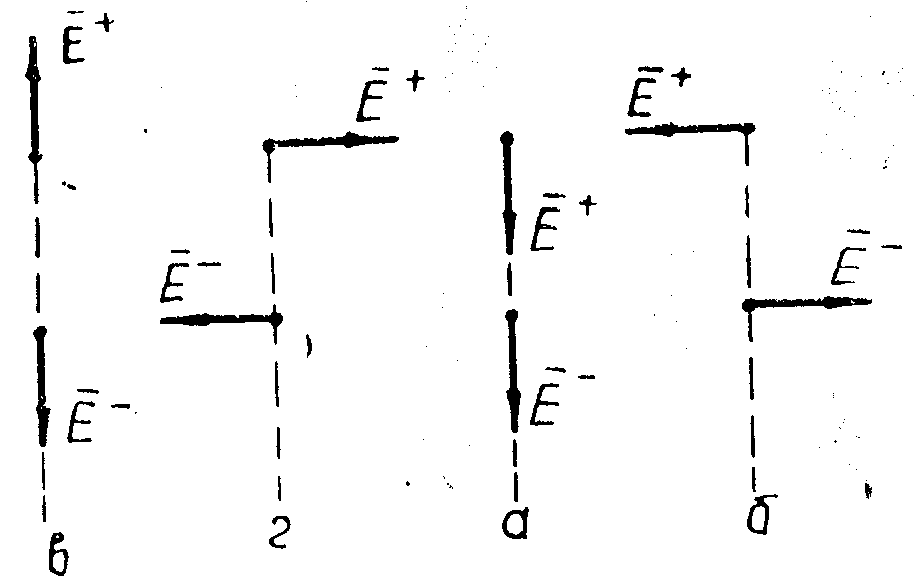 лечі 2 й 4, причому ці плечі збуджуються в противофазі. У плече 1 енергія не відгалужується. З теореми взаємності випливає, що при живленні моста одночасно через плечі 2 й 4 протифазними хвилями рівної амплітуди вся енергія піде в плече 3, а плече 1 збуджуватися не буде. Рис. 1.150

Ці властивості аналогічні третій і четвертій властивостям подвійного трійника. Кільцевому мосту властиві й інші, викладені вище, властивості подвійного трійника. При цьому передбачається, що кільцевий міст погоджений з боку будь-якого плеча.

З найдемо співвідношення між хвильовими опорами кільця Z і пліч Z₀, для яких на будь-якому вході моста, наприклад першому (рис. 1.148), немає відбиття в разі підключення до інших пліч узгоджених навантажень. Оскільки в площині третього плеча є вузол електричного поля, то можна вважати, що в цій площині міст закорочено, тому схему заміщення в разі збудження з боку плеча 1 можна подати так, як показано на рис. 1.151.

Опір лінії в перерізах 2 – 2 та 4 – 4 дорівнює хвильовому опору Z₀, оскільки до цих перерізів паралельно підключено чвертьхвильові короткозамкнені відрізки, вхідний опір яких нескінченний.

П

Рис. 1.151

ерерахувавши опір перерізу 2 – 2 до точок 1 – 1 маємо Z_вх = Z ²/Z_н = Z ²/Z₀.

Аналогічний вираз одержимо для опору перерізу 4 – 4, перерахованого до точок 1 – 1. Оскільки Е-плече включене в кільце послідовно, для узгодження моста за входом 1 – 1 потрібно, щоб виконувалась рівність Z₀ = 2Z_вх = 2Z ²/Z₀, звідки одержуємо Z₀ = Z Тому висота хвилеводу кільця – розмір b_кільця – менше розміру хвилеводів b_плеча в раз.

Застосування в кільцевих мостах трансформувальних властивостей відрізків довгих ліній зумовлює залежність їхніх характеристик від зміни частоти.

К ільцеві мости практично можуть застосовуватися для тих же цілей, що й подвійні трійники.

Н

Рис. 1.152

айбільш широке застосування кільцеві мости знайшли в схемах, виконаних на коаксіальних чи смужкових (рис. 1.152) хвилеводах, конструкції яких складається також з кільця довжиною 3/2 і чотирьох пліч, підключених до нього паралельно (рис. 1.153.а).

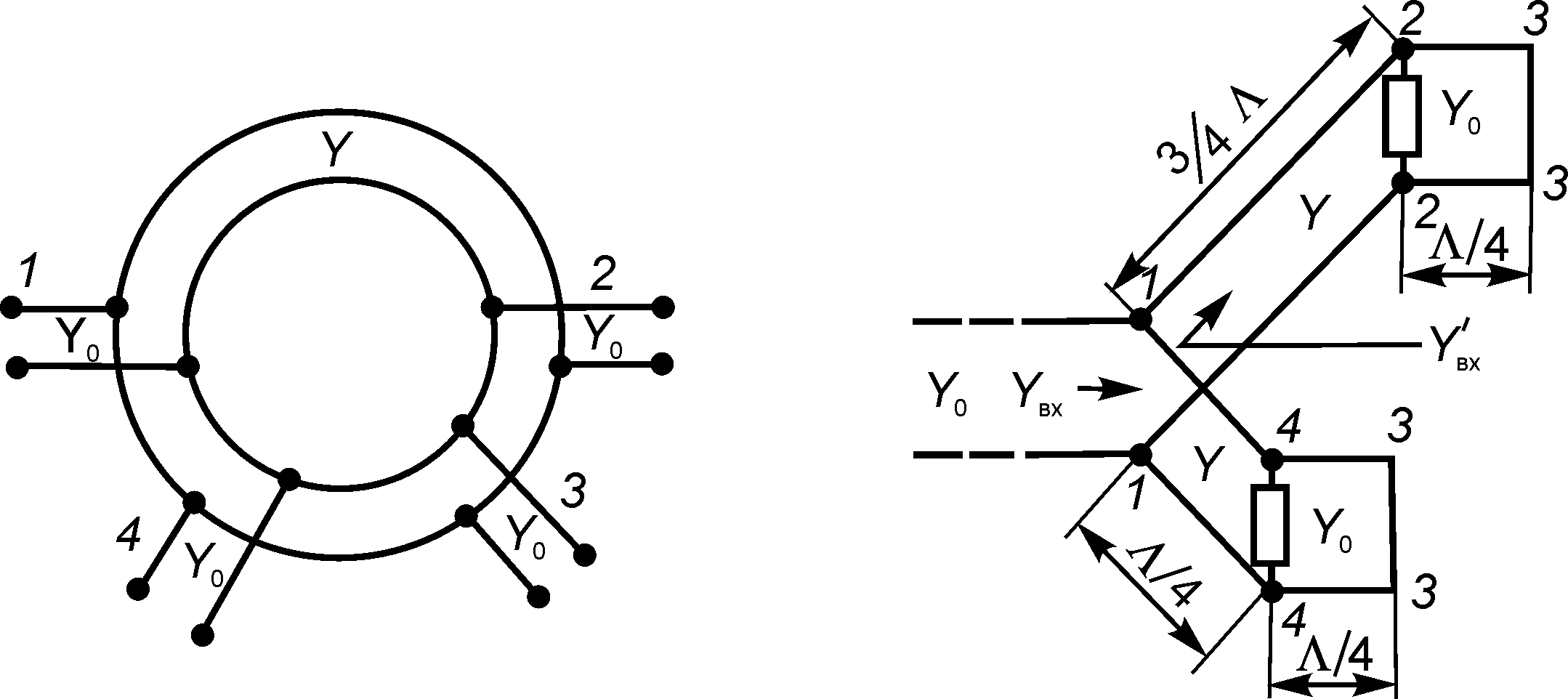Це кільцева лінія з хвильовою провідністю Y, до якої приєднані лінії з хвильовою провідністю Y₀.

a) б)

Рис. 1.153

Із плеча 1 до місць підключення ліній 2 та 4 хвилі приходять у фазі, тому потужність, що надходить із плеча 1, поділяється між ними нарівно. У плече 3 хвилі приходять двома шляхами, що відрізняються довжиною на /2 (по верхній частині кільця й по нижній). Тому в точках підключення лінії 3 виникає вузол поля, й енергія в цю лінію не передається  плечі 1 і 3 виявляються взаємно розв’язаними. Зв’язок значень хвильових провідностей вхідних ліній і кільця можна знайти, міркуючи так. Оскільки в площині плеча 3 є вузол електричного поля (вхідне плече – 1), то можна вважати, що в цій площині міст короткозамкнений, і тому схема заміщення має вигляд, показаний на рис. 1.153. б. Провідність ліній у перерізах 2 2 та 4 4 дорівнює хвильовій провідності Y₀, тому що паралельно цим перерізам підключено чвертьхвильові короткозамкнені в перерізі плеча 3 відрізки, вхідна провідність яких дорівнює нулю.

Перерахуємо провідність перерізу 2 2 до точок 1 1, використовуючи відомий з теорії довгих ліній вираз (див. модуль 1) для вхідної провідності лінії з хвильовою провідністю Y, навантаженої на провідність Y_н (у нашому випадку Y_н = Y₀):

А налогічний результат виходить для провідності перерізу 4 4, перерахованої до точок 1 – 1. Звідси випливає, що для забезпечення узгодження за входом 1 1 потрібно, щоб виконувалась рівність

а бо

Використання в кільцевих мостах властивостей трансформації опорів чвертьхвильовими відрізками довгих ліній визначає залежність їхніх характеристик від зміни частоти.

К

Рис. 1.154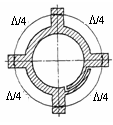

ільцевий міст із «перекиданням фази» (рис. 1.154). Загальна довжина кільця розглянутих вище мостів становить 1,5. Цей розмір може виявитися неприйнятним для ПНВЧ дециметрового діапазону хвиль. Його зменшують, замінюючи ділянку кільця довжиною 3/4 відрізком зв’язаних ліній з l = /4, що вносить такий самий фазовий зсув 3/2, оскільки зв’язок дає додатковий зсув фаз на . Відзначимо, що обидва кінці цього відрізка мають бути заземлені, що не завжди зручно.

Мости з «перекиданням фази» мають більшу широкосмуговість, бо довжина їх кільця не 1,5, а .

Мости на основі 3-децибельних спрямованих відгалужувачів компактніші, однак їх мікросмужкове виконання утруднене, тому що ширина зазору між смужками має бути лише 8...10 мкм.