2). Данное уравнение решаем, применяя общий алгоритм:
a0. Примем: z = y–n+1, где (–n+1)= –3; то есть: z= y–3.
a1. Запишем преобразованное уравнение Бернулли: z′–sinx∙z= 3sinx. (3)
a2. Решение уравнения ищем в виде функции: z=u(x)∙v(x);
a3. Вычислим интеграл: – = =–cosx → u= =e–cosx.
a4.
Вычислим функцию v: v =
=
+
С = –3
+
С =
=–3ecosx +С;
a5. Запишем общее решение уравнения для (3): z=u∙v= e–cosx (–3ecosx +С). (4)
a6. Учитывая: z= y–3, запишем общее решение для (1): y–3=Ce–cosx –3.
a4. Запишем частное решение уравнения: y–3=4e–cosx –3, так как С=4.
Ответ: y–3=Ce–cosx –3 – общее решение; частное решение: y–3=4e–cosx –3.
Пример 9–180: Найти уравнение кривой, проходящей через точку (0,1), если площадь треугольника, образуемого осью абсцисс, касательной и радиус-вектором точки касания, постоянна и равна 1.
Решение:
В Примере
1–19
получено выражение:
отрезка Т=OТ=
,
–
отсекаемого касательной
на оси абсцисс.
1). Так как площадь треугольника вычисляется по формуле: S= ah, где a–основание, h – высота треугольника, условие задачи запишем так:
▪
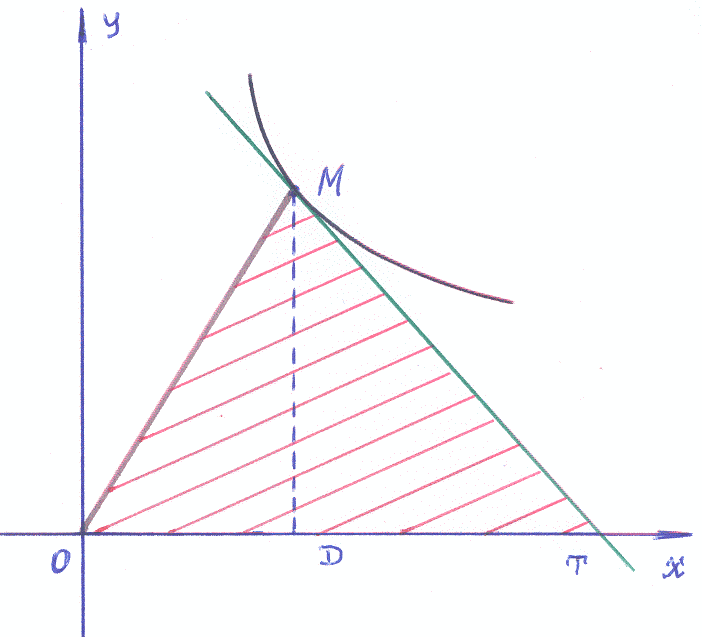ОТ∙ND=2S=2
→
∙y
=2; (1)
▪ ОT∙ND=2S=–2 → ∙y =–2 (2)
Случай-1.
2). Запишем (1),
в виде: x′–
x=–
–
«стандартная форма»
линейного уравнения.
a0. Решение уравнения ищем в виде функции: x=u∙v.
a1. Вычислим интеграл: – = =ln|y| → u=y.
a2.
Вычислим функцию v: v =
+С=–2
+С
=y–2+С.
a3. Запишем общее решение уравнения: x=u∙v=y ∙(y–2+С)= +Cy.
a4. Запишем частное решение уравнения: x= –y, при С=–1.
Случай-2.
3). Запишем (2), в виде: x′– x= – «стандартная форма» линейного уравнения.
a0. Решение уравнения ищем в виде функции: x=u∙v.
a1. Вычислим интеграл: – = =ln|y| → u=y.
a2. Вычислим функцию v: v = +С=2 +С =–y–2+С;
a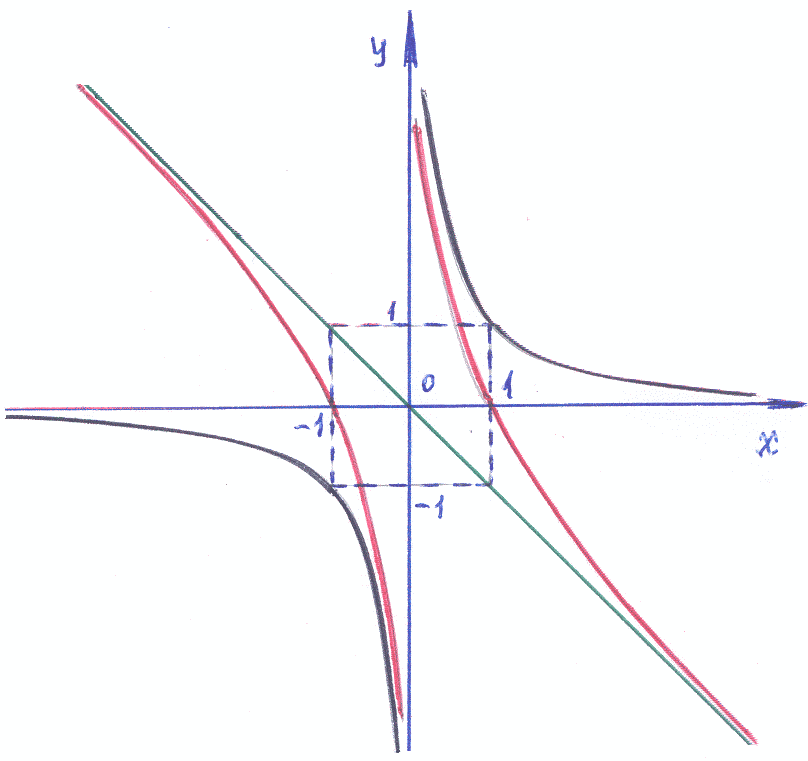
3. Запишем
общее решение уравнения: x=u∙v=y∙(С–y–2)=Cy–
.
Это решение «симметрично
относительно оси ОХ» решению, полученному
в Случае-1.
a4. Запишем частное решение уравнения: x=y– , при С=1.
4). Построим эскиз графика функции x= –y, используя известные графики для гиперболы и прямой и применяя понятие «сумма функций» (см. рисунок: выделено красным).
Ответ: для Случая-1: x= –y – частное решение ДУ; для Случая-2: x= y – – частное решение ДУ.
Замечание: Если не заметить присутствия двух различных вариантов решения рассмотренной задачи, то «зеркальное решение» будет потеряно. В задачах физики это дополнительно подсказывает важность понимания начальных условий исследуемого процесса: возможно исследователю потребуются дополнительные эксперименты для уточнения особенностей протекания процесса.
Пример
10–198:
Сила тока i в цепи с
сопротивлением R,
индуктивностью L и
напряжением u удовлетворяет
уравнению: L∙
+
R∙i
= u. Найти силу тока
i в момент времени t,
если u=
Esinωt
и i
= 0 при t
= 0 (L,
R, E,
ω –
постоянные).
Решение:
1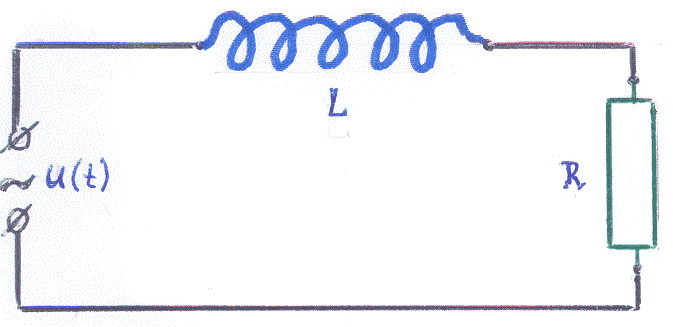
).
Приведём уравнение к «стандартной
форме»:
i′ + a∙i = b∙u: (1)
где a=
и b=
(принято для удобства записи).
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде: функцию i=z∙v.
a1.
Вычислим интеграл:
–
=–a
=–at
→ z=
=e–at.
a2.
Вычислим функцию v: v=
+С=b
+С=bE
+С.
Вычислим интеграл: J=
=[дважды
применяется «интегрирование по частям»,
затем решение алгебраического равенства
относительно символа J]=
eat∙(a∙sinωt–ω∙cosωt).
Тогда окончательно: v=bE∙J+С,
или v=bE∙J+bE∙С=bE∙(J+С).
Последнее определяется «удобством!»:
допустимо, так как bE
– постоянная величина!
a3. Запишем общее решение уравнения: i=u∙v=bE∙e–at∙(J+С). (2)
a4.
Запишем частное решение уравнения из
условия: i(0)=0 → легко вычисляется
С=
→ частное решение: i=bE∙
(a∙sinωt–ω∙cosωt+ω∙e–at).
С учетом значений a
и b получим окончательно:
i=
(R∙sinωt–Lω∙cosωt+Lω∙
).
Ответ: i= (R∙sinωt–Lω∙cosωt+Lω∙ ) – частное решение.
☻
Вопросы для самопроверки:
Как определяют линейное дифференциальное уравнение 1-го порядка?
Что значит: «стандартная форма» линейного уравнения, зачем её вводят?
Какова основная «идея» способа «подстановки» решения линейного уравнения?
Всегда ли можно «проинтегрировать» линейное ДУ?
Какие уравнения относят к уравнениям Бернулли?
В чем особенность интегрирования уравнения Бернулли?
Бывают ли уравнения Бернулли, которые невозможно «проинтегрировать»?
< * * * * * >