Домашнее задание
Дома |
Л-2 |
гл.10: № 70, 71, 72, 75, 85, 87, 89, 94, 180, 198. |
10 |
Пример 1–70: Решить дифференциальное уравнение: (1+ x2)y′= 2xy+(1+ x2)2. (1)
Решение:
1). Так как
заданное уравнение не «стандартной
формы», приводим его к стандартной
форме: y′+P(x)∙y=Q(x),
то есть: y′–
y=
x2+1. (2)
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1. Вычислим интеграл: – и запишем: u= .
a2.
Вычислим функцию v: v =
+С.
a3.
Запишем общее решение уравнения: y=u∙v=
∙
.
3). В нашем случае: уравнение линейное, имеет «стандартную форму»: y′+P(x)∙y=Q(x)!
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1.
Вычислим интеграл: –
=–
=–ln(x2+1)
→ u=
=
x2+1.
a2.
Вычислим функцию v: v =
+С=
+С
= x +С.
a3. Запишем общее решение уравнения: y=u∙v=(x2+1)∙(x +С).
Ответ: y=u∙v=(x2+1)∙(x +С) – общее решение.
Пример 2–71: Решить дифференциальное уравнение: y′ +2y =e3x.
Решение:
1). Уравнение записано в «стандартной форме».
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1.
Вычислим интеграл: –
=–
=–2x
→ u=
=
e–2x.
a2.
Вычислим функцию v: v =
+С=
+С
=
e5x
+С.
a3.
Запишем общее решение уравнения: y=u∙v=
e–2x
∙
=
e3x
+Сe–2x.
Ответ: y= e3x +Сe–2x – общее решение.
Пример 3–72: Решить дифференциальное уравнение: y′ + =2lnx +1.
Решение:
1). Приведём уравнение к «стандартной форме»: y′ + y =2lnx +1.
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1.
Вычислим интеграл: –
=–
=–
lnx → u=
=
.
a2.
Вычислим функцию v: v=
+С=
+С
=2
+
+С.
Если учесть «табличный» интеграл (легко
получить интегрированием по частям!):
=
=
lnx–
,
то: v=x2lnx+
–
+С
=x2lnx+С.
a3.
Запишем общее решение уравнения: y=u∙v=
∙
=
xlnx +
.
Ответ: y= xlnx + – общее решение.
Пример 4–75: Решить дифференциальное уравнение: (1+ x2)dx=(arctgy–x)dy.
Решение:
1). Видим, что
по y и y′
уравнение не приводится
к линейному уравнению. Приведём уравнение
к «стандартной форме» линейного по по
x и x′:
x′ +
x
=
.
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1.
Вычислим интеграл: –
=–
=–
arctgy → u=
=
.
a2. Вычислим
функцию v: v=
+С=
+С=[Примем:
arctgy=t]= =
+С=[см.
таблицу интегралов!]=tet–et+С=
arctgy
–
+С.
a3.
Запишем общее решение уравнения: y=u∙v=
∙
=
=arctgy–1+C
Ответ: y= arctgy–1+C – общее решение.
Пример
5–85:
Решить дифференциальное уравнение: y′
=
,
y(1)=1.
Решение:
1). Видим, что по y и y′ уравнение не приводится к линейному уравнению. Приведём уравнение к «стандартной форме» линейного по по x и x′: x′ + x =2lny+1.
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: x=u∙v.
a1.
Вычислим интеграл: –
=–
=–
lny → u=
=
.
a2.
Вычислим функцию v: v=
+С=
+С
=2
+
+С.
Если учесть результат Примера
3–72,
то: v= y2lny+С.
a3.
Запишем общее решение уравнения: x=u∙v=
∙(y2lny+С)
= ylny
+
.
a4. Запишем частное решение уравнения: x = ylny + , так как С=1.
Ответ: x = ylny + – общее решение; частное решение: x = ylny + .
Пример 6–87: Решить дифференциальное уравнение: dy =(y2ex–y)dx. (1)
Решение:
1). Из исходного уравнения: y=0–решение. Перепишем (1): y′+y =ex∙y2. (2)
2). Получили уравнение (2) Бернулли в «стандартной форме», для n=2.
a0. Примем: z = y–n+1, где (–n+1)= –1; то есть: z= y–1.
a1. Запишем преобразованное уравнение Бернулли: z′–z= – ex. (3)
a2. Решение уравнения ищем в виде функции: z=u(x)∙v(x);
a3.
Вычислим интеграл: –
=
=x
→ u=
=
ex.
a4.
Вычислим функцию v: v =
=
+С=
– x
+С;
a5. Запишем общее решение уравнения для (3): z=u∙v= ex ∙( С–x). (4)
a6. Учитывая: z= y–1, запишем общее решение для (1): y–1=ex ∙( С–x).
Ответ: yex ∙( С–x)=1 – общее решение уравнения, также y=0.
Пример
7–89:
Решить дифференциальное уравнение: y′
=
yctgx+
. (1)
Решение:
1). Из исходного
уравнения: y=0–решение.
Перепишем (1):
y′–ctgxy
=
∙y3. (2)
2). Получили уравнение (2) Бернулли в «стандартной форме», для n=3.
a0. Примем: z = y–n+1, где (–n+1)= –2; то есть: z= y–2.
a1. Запишем преобразованное уравнение Бернулли: z′+ctgx∙z= –2 . (3)
a2. Решение уравнения ищем в виде функции: z=u(x)∙v(x);
a3.
Вычислим интеграл: –
=–2
=–2ln|sinx|
→ u=
=
.
a4.
Вычислим функцию v: v =
=
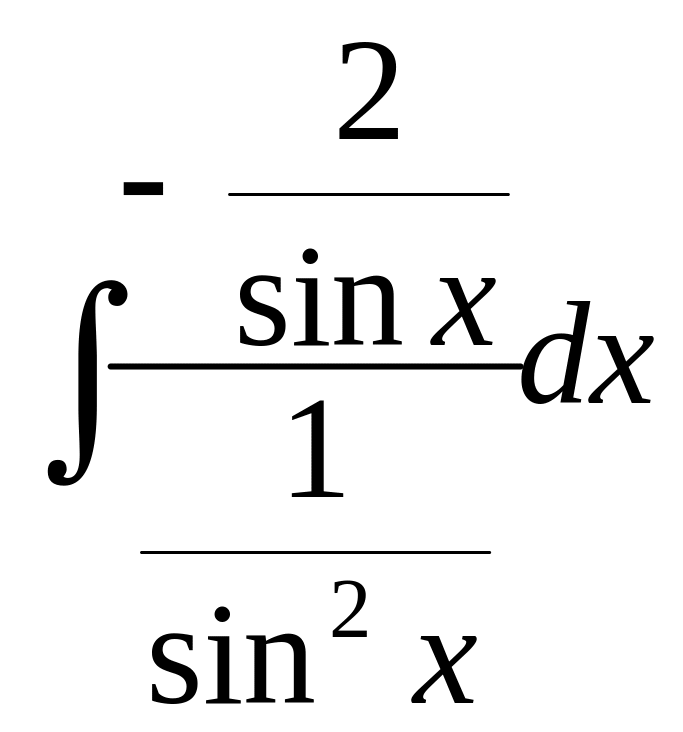+С=–2
+С=2cosx+C;
a5. Запишем общее решение уравнения для (3): z=u∙v= (2cosx+C). (4)
a6. Учитывая: z= y–2, запишем общее решение для (1): y–2= (2cosx+C).
Ответ: sin2x= y2(2cosx+C) – общее решение уравнения, также y=0.
Пример
8–94:
Решить дифференциальное уравнение:
3dy=
–(1+3y3)y∙sinxdx,
y
=1. (1)
Решение:
1). Из исходного
уравнения: y=0–решение.
Перепишем (1):
y′+
sinx∙y
=
–sinx∙y4. (2)