
- •Кинематика
- •Кинематика точки
- •Способы задания движения точки
- •Векторный способ задания движения точки
- •Координатный способ задания движения точки
- •Частный случай задания движения точки в полярной системе координат
- •1.1.3. Траекторный (естественный) способ задания движения точки
- •Определение пути s(t), пройденного точкой по траектории
- •Скорость точки при различных способах задания ее движения
- •1.2.1. Скорость точки при векторном способе задания ее движения
- •1.2.2. Скорость точки при координатном способе задания ее движения
- •1.2.3 Скорость точки при траекторном способе задания ее движения
- •1.3.2. Ускорение точки при координатном способе задания ее движения
- •Понятие о сопровождающем (естественном) трехграннике
- •1.3.3. Ускорение точки при естественном способе задания ее движения
- •Кинематические уравнения движения точки по траектории (закон скоростей и закон траекторных координат)
- •Способы задания движения точки и кинематические характеристики
- •Расчетно-графическая работа к 1 Кинематика точки
- •Простейшие движения твердого тела
- •2.1. Степени свободы
- •2.2. Поступательное движение твердого тела
- •2.3. Вращение твердого тела вокруг неподвижной оси
- •2.3.1 Угловая скорость и угловое ускорение тела
- •2.3.2 Скорость и ускорение любой точки твердого тела при его вращении вокруг неподвижной оси
- •Плоское движение твердого тела
- •3.1. Уравнения движения, угловая скорость и угловое ускорение твердого тела при плоском движении
- •3.2. Скорости точек твердого тела при плоском движении
- •3.2.1. Метод полюса
- •3.2.2. Метод мгновенного центра скоростей
- •3.2.3. Определение положения мгновенного центра скоростей
- •3.4. Расчетно-графическая работа к2 Кинематика плоского движения
- •3.4.1. Схемы конструкций и исходные данные
- •Продолжение табл.3.4.1
- •Окончание табл. 3.1.1
- •3.4.2. Указания и план выполнения
- •3.4.3. Пример выполнения расчетно-графической работы к2 Кинематика плоского движения
- •4.2. Углы Эйлера
- •4.2.1.Формулы преобразования координат. Поворотные матрицы
- •4.2.2. Мгновенная угловая скорость и угловое ускорение. Кинематические уравнения Эйлера
- •4.2.3. Скорость и ускорение точек тела. Формула Ривальса
- •4.3. Расчетно-графическая работа к3 Кинематика вращательного движения твердого тела вокруг неподвижной точки (случай регулярной прецессии).
- •4.3.1.Схемы конструкций и исходные данные
- •4.3.2. Указания и план выполнения
- •4.3.3. Примеры выполнения расчетно-графической работы к3 (регулярная прецессия)
- •4.4. Общий случай движения твердого тела
- •6. Сложное движение точки
- •6.1. Относительное, переносное и абсолютное движения точки
- •6.2. Зависимости между скоростями и ускорениями точек в относительном, переносном и абсолютном движениях
- •6.3. Расчетно-графическая работа к4 Кинематика сложного движения точки при переносном вращательном движении
- •6.3.1. Схемы конструкций и исходные данные
- •6.3.2. Указания и план выполнения
- •6.3.3. Пример выполнения расчетно-графической работы к4 сложное движение точки при переносном вращательном движении
- •1. Кинематические характеристики точки м в относительном движении
- •2. Кинематические характеристики точки м в переносном вращательном движении
- •Литература Основная
- •Дополнительная
- •Образец оформления титульного листа
- •Кинематика Расчетно-графическая (курсовая) работа
- •1. Кинематика точки……………………………………………..2
- •1.1. Способы задания движения точки…………………………………3
- •1.4. Кинематические уравнения движения точки по траектории (закон скоростей и закон траекторных координат) ……………15
- •6.2. Зависимости между скоростями и ускорениями точек в относительном, переносном и абсолютном движениях……
6. Сложное движение точки
6.1. Относительное, переносное и абсолютное движения точки
В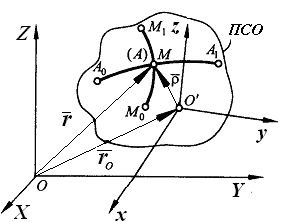 ряде задач механики требуется рассмотрение
движения точки одно
ряде задач механики требуется рассмотрение
движения точки одно
временно в нескольких системах отсчета, из которых одна условно принимается за неподвижную (АСО), а связанную с ней систему координат
Рис.6.1.
OXYZ
с единичными
ортами
![]() ,
а другая определенным образом движется
относительно принятой неподвижной
системы отсчета и
,
а другая определенным образом движется
относительно принятой неподвижной
системы отсчета и
ее принимают за подвижную систему
отсчета(ПСО),
а связанную с ней систему
координат О’
xyz
с единичными ортами
![]() .
Движение точки М называется сложным,
если точка перемещается относительно
подвижной системыО’xyz,
неизменно
связанной с некоторым телом,
принятым за
(ПСО),
которое в свою очередь движется
относительно неподвижной
системы отсчета (АСО) и связанной
с ней системы координат
OXYZ
(рис. 6.1)
.
Движение точки М называется сложным,
если точка перемещается относительно
подвижной системыО’xyz,
неизменно
связанной с некоторым телом,
принятым за
(ПСО),
которое в свою очередь движется
относительно неподвижной
системы отсчета (АСО) и связанной
с ней системы координат
OXYZ
(рис. 6.1)
Несколько примеров сложного движения точки:
движение человека, идущего по эскалатору метро относительно стены туннеля (относительно неподвижной системы отсчета (АСО) OXYZ является сложным, так как человек движется относительно эскалатора подвижной системы отсчета (ПСО) О’xyz и вместе с эскалатором относительно неподвижной стены неподвижной системы отсчета (АСО) OXYZ;
аналогичным образом могут быть представлены движение человека, корабля, плывущего по реке, относительно неподвижного берега;
движение снаряда в канале ствола орудия при одновременном вращении ствола в процессе слежения за целью и т.д.
1. Движение
точки М относительно подвижной
системы отсчета (ПСО)
О’xyz
называется относительным,
а скорость и ускорение точки в этом
движенииотносительной
скоростью (![]() )
и
относительным ускорением (
)
и
относительным ускорением (![]() ),
которые определяются по формулам
раздела1 «Кинематика точки» в зависимости
от способов задания движения точки (см.
табл.1.1).
),
которые определяются по формулам
раздела1 «Кинематика точки» в зависимости
от способов задания движения точки (см.
табл.1.1).
2. Движение
подвижной
системы отсчета (ПСО)
О’xyz
относительно неподвижной
системы отсчета (АСО)
OXYZ
называется переносным, а
скорость и ускорение той неизменно
связанной с подвижной системой отсчета
точки (А), с которой в данный момент
совпадает движущаяся точка М,
называются
скоростью (![]() )
и ускорением
(
)
и ускорением
(![]() )
точки М
в переносным
движении, которые
определяются по формулам раздела
«Кинематика твердого тела» в зависимости
от вида движения твердого тела
поступательное, вращательное вокруг
неподвижной оси или неподвижной точки,
плоскопараллельное, общий случай
движения (разд.2-5).
)
точки М
в переносным
движении, которые
определяются по формулам раздела
«Кинематика твердого тела» в зависимости
от вида движения твердого тела
поступательное, вращательное вокруг
неподвижной оси или неподвижной точки,
плоскопараллельное, общий случай
движения (разд.2-5).
Так, в примере движения человека, идущего по эскалатору метро, скоростью ( ) человека в переносном движении будет скорость ступеньки, на которой он находится в данный момент времени.
3. Движение
точки М относительно неподвижной
системы отсчета (АСО)
OXYZ
называется
абсолютным (сложным), а
скорость и ускорение точки в этом
движении
абсолютной
скоростью (![]() )
и абсолютным
ускорением (
)
и абсолютным
ускорением (![]() ).
).
6.2. Зависимости между скоростями и ускорениями точек в относительном, переносном и абсолютном движениях
В задачах кинематики сложного движения точки требуется установить зависимости между скоростями и ускорениями точки в относительном, переносном и абсолютном движениях.
Для этого необходимо установить связь между изменениями вектора в подвижной и неподвижной системах отсчета.
Положение точки М относительно
неподвижной
системы отсчета (АСО)
OXYZ
задано вектором
![]() с началом в точке О,
тогда абсолютная
траектория точки М
с началом в точке О,
тогда абсолютная
траектория точки М
![]() является
годографом радиус-вектора
(рис.6.1),
а абсолютные скорость и ускорения точки
М определяются выражениями
является
годографом радиус-вектора
(рис.6.1),
а абсолютные скорость и ускорения точки
М определяются выражениями
![]()
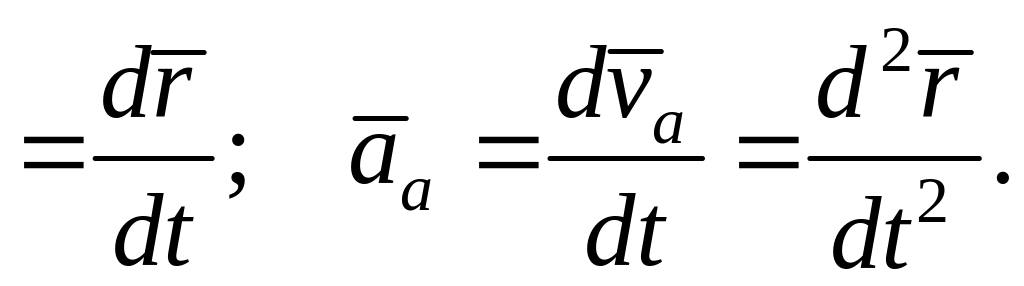 (6.1)
(6.1)
Положение точки М относительно
подвижной
системы отсчета (ПСО)
О’xyz
задано радиус-вектором
![]() с началом в точке О’,
тогда
относительная траектория точки М
с началом в точке О’,
тогда
относительная траектория точки М
![]() является
годографом радиус-вектора
(рис.6.1), а относительные скорость и
ускорения точки М определяются
по формулам (см. табл.1.1) раздела (глава1)
«Кинематика точки» следующими
выражениями:
является
годографом радиус-вектора
(рис.6.1), а относительные скорость и
ускорения точки М определяются
по формулам (см. табл.1.1) раздела (глава1)
«Кинематика точки» следующими
выражениями:
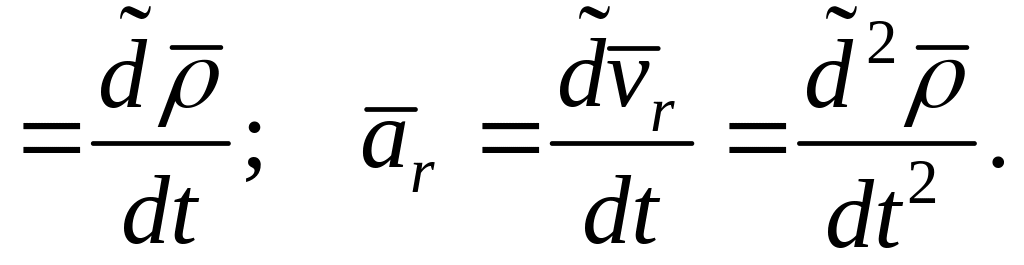 (6.2)
(6.2)
Скорость ( ) и ускорение ( ) точки М в переносная движении определяются по формулам раздела «Кинематика твердого тела» в зависимости от его вида движения поступательное, вращательное вокруг неподвижной оси или неподвижной точки, плоскопараллельное, общий случай движения (главы 2-5).
Сформулируем теоремы о сложении скоростей и ускорений точки в сложном ее движении (без вывода).
Абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей:
![]() (6.3)
(6.3)
Абсолютное ускорение точки является векторной суммой трех ускорений: относительного, ускорения точки в переносном движении и ускорения Кориоли’са:
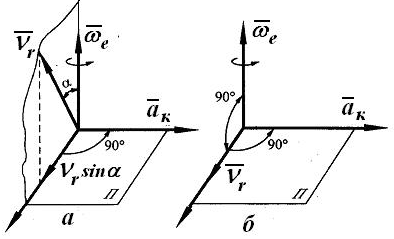 Рис.6.2
Рис.6.2
![]() ,
где (6.4)
,
где (6.4)
ускорение Кориолиса
![]() .
(6.5)
.
(6.5)
Ускорение Кориолиса
есть векторная физическая величина,
равная удвоенному
векторному произведению угловой скорости
![]()
переносного движения, перенесенной в
рассматриваемую точку М, на вектор
переносного движения, перенесенной в
рассматриваемую точку М, на вектор
![]()
относительной скорости точки.
относительной скорости точки.
Согласно общему
правилу векторного произведения, вектор
![]() направлен перпендикулярно плоскости,
в которой
лежат векторы
и
(рис.6.2,а), в
ту сторону,
откуда поворот от
к
на
наименьший угол кажется против хода
часовой стрелки. Если угол между векторами
и
обозначить
направлен перпендикулярно плоскости,
в которой
лежат векторы
и
(рис.6.2,а), в
ту сторону,
откуда поворот от
к
на
наименьший угол кажется против хода
часовой стрелки. Если угол между векторами
и
обозначить
![]() ,
то по модулю ускорение Кориолиса равно
,
то по модулю ускорение Кориолиса равно
![]() (6.6)
(6.6)
Остановимся на частных случаях, когда ускорение Кориолиса
максимальное:
![]() (6.7)
(6.7)
обращается в нуль:
1)
![]() т.е. переносное движение
поступательное;
т.е. переносное движение
поступательное;
2)
![]() ,
т.е. в те моменты
времени, когда в относительном движении
точка остановилась, например, при
изменении направления относительного
движения;
,
т.е. в те моменты
времени, когда в относительном движении
точка остановилась, например, при
изменении направления относительного
движения;
3)
![]() когда вектор скорости
относительного движения
параллелен вектору угловой скорости
переносного вращения
когда вектор скорости
относительного движения
параллелен вектору угловой скорости
переносного вращения
![]() (
).
(
).
