4.3.2. Указания и план выполнения

Случай регулярной прецессии – это такое вращение твердого тела вокруг неподвижной точки, при котором (рис.4.3.2) во все время движения остаются постоянными:

• угол нутации 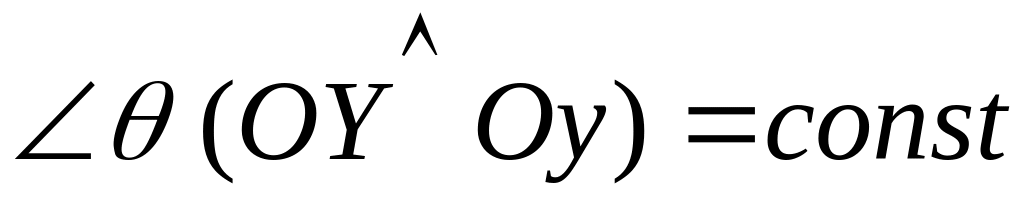, поэтому ;

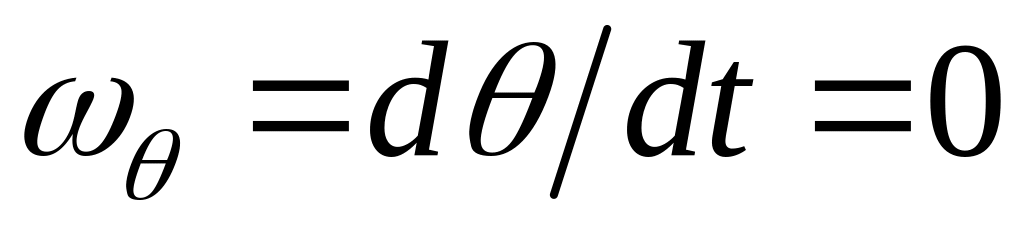 угловые скорости прецессии, ротации и мгновенная угловая скорость

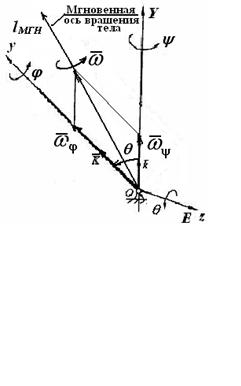
Рис.4.3.2

 угловое ускорение .

1. Найти неподвижную точку О вращающегося тела, выбираемую за начало отсчета неподвижной и связанной координатных систем. Выбрать оси прецессии , ротации , нутации (   или  ).

2. Определить угловые скорости нутации , прецессии , ротации и мгновенную угловую скорость и мгновенную ось вращения .

В зависимости от задания движения твердого тела вектор можно определять двумя способами:

1) по ее составляющим ;

2) использовать мгновенную ось вращения , которую в дальнейшем будем для краткости обозначать . По известной скорости какой-либо точки М твердого тела и положению оси = находят величину : , где –перпендикуляр, опущенный из точки М на ось = .

3. Определить угловое ускорение твердого тела. В случае регулярной прецессии и является закрепленным в точке О вектором, положительное направление которого определяется как результат векторного произведения.

4. Определить скорости произвольных точек твердого тела по формуле Эйлера , величина которой .

5. Определить ускорения произвольных точек твердого тела по формуле , где  вектор осестремительного ускорения, величина которого  вектор вращательного ускорения, величина которого .

Так как всегда направлено от точки по радиусу к оси , можно не пользоваться векторной формой для . Что же касается , то его следует находить только по векторной форме.

Поскольку при вращении тела около полюса вектор неколлинеарен , то и , вообще говоря, не являются перпендикулярными векторами, поэтому определение должно производиться после построения векторов на чертеже, и величина ускорения будет равна

.

. Для точек, лежащих на оси ротации твердого тела, справедливы также следующие зависимости:

и , где – нормальное ускорение; – касательное ускорение; при регулярной прецессии .

Все векторы, лежащие в плоскости OXY (плоскости чертежа), должны быть изображены в этой плоскости; направление же других векторов должно быть указано в тексте.

4.3.3. Примеры выполнения расчетно-графической работы к3 (регулярная прецессия)

Пример 1. Дано. Конус 1 с углом 2 = 60 при вершине (рис.4.6.3) катится по неподвижному конусу 2 с углом 2=120 при вершине без скольжения, обегая последний 120 раз в минуту, при этом вершина О конуса 1 остается неподвижной, а центр С его основания движется по окружности, расположенной в горизонтальной плоскости. Высота конуса 1 ОС=10 см.

Определить. 1. Угол нутации , угловые скорости нутации , прецессии , ротации и мгновенную угловую скорость .

2. Угловое ускорение конуса .

3. Скорости точек А, В, С

4. Ускорения точек А, В, С  (найти осестремительное  и вращательное  ускорения точки С).

Решение. Введем неподвижную систему координат OXYZ с началом в точке О конуса 1 (рис.4.3.3) . Поскольку конус 1 катится по неподвижному конусу 2 без скольжения, то скорости всех его точек, лежащих на образующей ОА, равны в данный момент времени нулю. Следовательно, мгновенная ось вращения конуса 1 совпадает с образующей ОА.

1.Угол нутации , поскольку с конца оси нутации

ОЕ поворот от оси прецессии OY к оси ротации Oy кажется по часовой

стрелке;

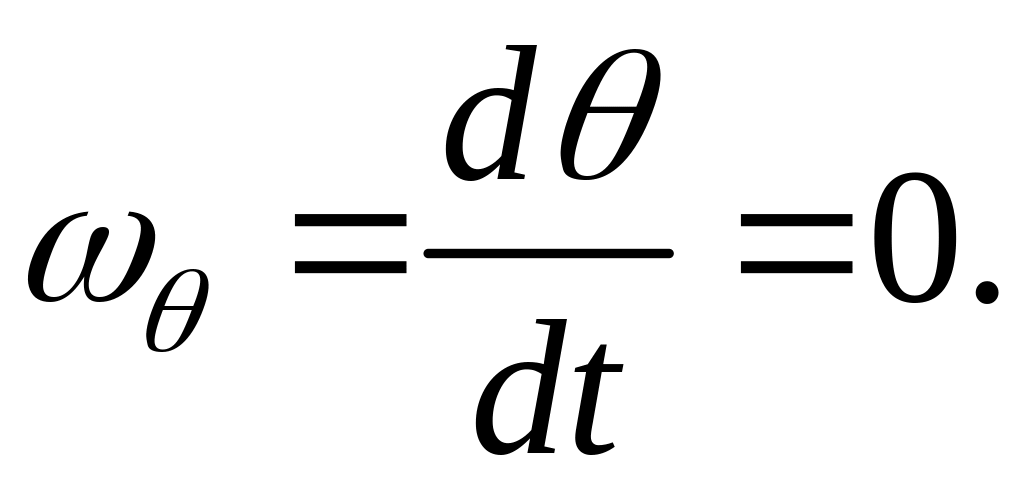
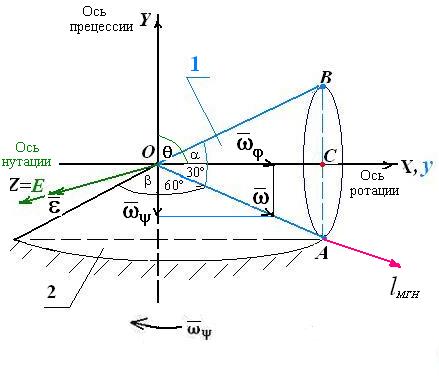Рис.4.3.3.

2. Величина угловой скорости прецессии .

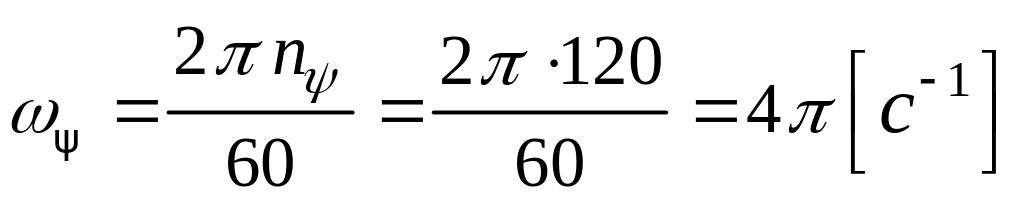
Направление вектора определим в зависимости от задания движения конуса 1, в данном случае вращение конуса 1 вокруг оси прецессии происходит по часовой стрелке, поэтому  (оси прецессии).

3. Векторное равенство , в котором линии действия всех его составляющих известны, позволяет определить как направление векторов всех составляющих угловых скоростей, так и их величины а именно: линией действия вектора является мгновенная ось вращения ; линией действия вектора   ось прецессии OY, линией действия вектора  ось ротации Оy (рис.4.3.3). Таким образом, величина мгновенной угловой скорости 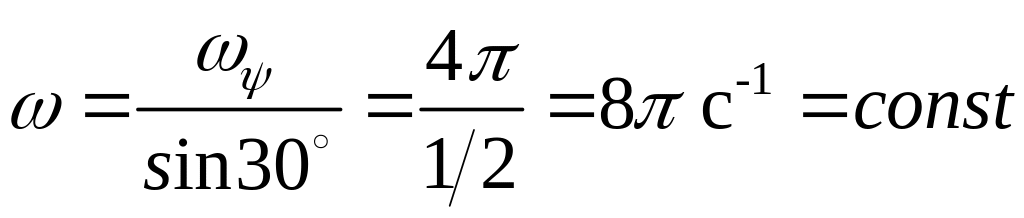, а величина угловой скорости ротации

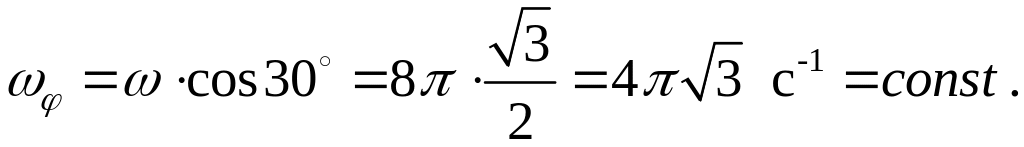
4. Угловое ускорение в случае регулярной прецессии определяется векторным произведением , т.е. вектор  , так как с конца оси OZ=ОЕ поворот от вектора к вектору кажется против хода часовой стрелки. Величина углового ускорения

рад/с² .

5. Скорости точек конуса 1 (рис.4.3.4)

5.1) точка А , так как в данный момент времени эта точка принадлежит мгновенной оси вращения конуса 1;

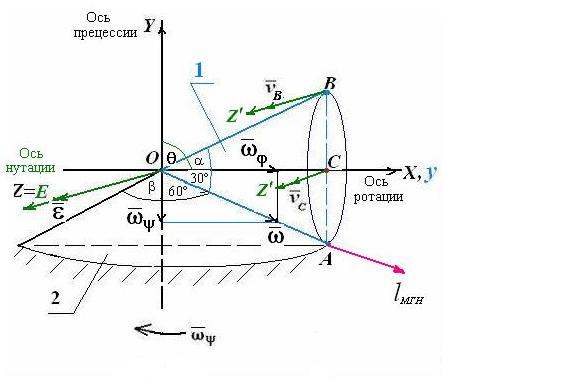Рис.4.3.4

5.2) точка В  , где ,

и вектор  .

5.3) точка С I Траекторией точки С, с одной стороны, является окружность, плоскость которой перпендикулярна мгновенной оси вращения и центр которой лежит на , с другой стороны, – окружность, плоскость которой перпендикулярна оси прецессии ОY и центр которой лежит на этой оси. Поэтому

, (I)

где – кратчайшее расстояние от точки С до мгновенной оси ; =

. Вектор , так как направление вектора совпадает с направлением мгновенной оси = ОА и вектор направлен таким образом, чтобы с конца этой оси = вращение конуса 1 казалось против хода часовой стрелки (рис.4.3.4).

II С другой стороны, поскольку точка С- центр основания конуса 1 движется по окружности, расположенной в горизонтальной плоскости, то

, (II)

где – кратчайшее расстояние от точки С до оси ОY, равное

,

6. Ускорение какой-либо точки конуса 1 определим как геометрическую сумму осестремительного и вращательного ускорений (рис.4.3.5) .

6.1) точка А: ; так как ,

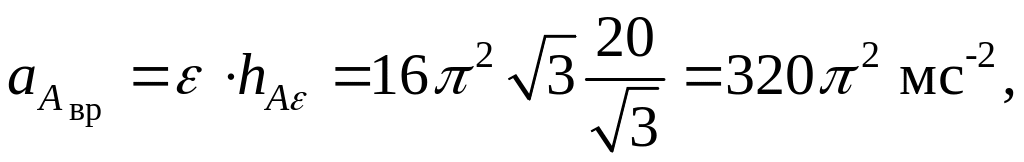где; м.

Вектор направлен перпендикулярно плоскости, в которой лежат векторы и , т.е. перпендикулярно ОА в сторону .

Таким образом, ;

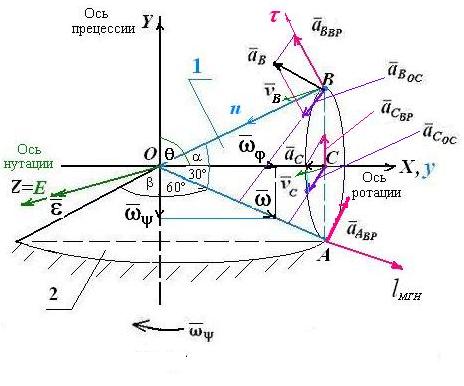 6.2) точка В: ;

Рис.4.3.5

;

Вектор направлен от точки B радиусу к мгновенной оси вращения конуса 1 (рис.4.3.5).

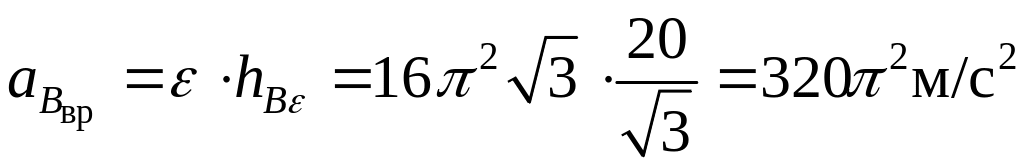, где м.

Вектор перпендикулярен плоскости, в которой лежат векторы и , принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОB в сторону .

Полное ускорение точки B найдем как диагональ прямоугольника, построенного на векторах :

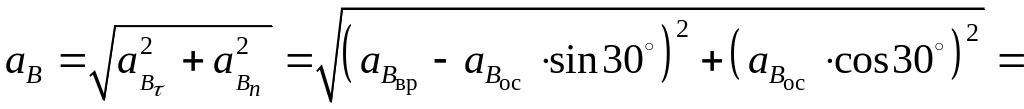
6.3) точка С: I  ;

.

Вектор направлен от точки С по радиусу к мгновенной оси вращения кoнуса 1. Вектор перпендикулярен плоскости, в которой лежат векторы и , принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОС в сторону (рис.4.3.5);

II ;

Ответ. 1).  =- /2; =0; 1/с; 1/с; 1/с.

2) 1/с².

3). .

4) ;

; .

Пример 2 выполнения расчетно-графической работы К3

Дано. Конус 1 с углом 2=60 при вершине (рис. 4.3.6) катится без скольжения по неподвижному конусу 2 с углом 2=120 при вершине, при этом вершина О конуса 1 остается неподвижной, а центр С его основания движется по окружности, расположенной в горизонтальной плоскости, с постоянной скоростью , причем =3 м/с, ОА=ОВ=2м.

Определить. 1. Угол нутации, угловую скорость нутации , прецессии , ротации , мгновенную угловую скорость . 2. Угловое ускорение конуса 3. Скорости точек А и В , 4. Ускорения точек А, В, С , , , а также (найти осестремительное и вращательное ускорения точки С).

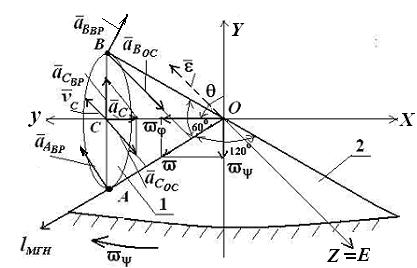
Рис. 4.3.6

Решение. Введем неподвижную систему координат OXYZ с началом в точке О конуса 1. Поскольку конус 1 катится по неподвижному конусу 2 без скольжения, то скорости всех его точек, лежащих на образующей ОА, равны в данный момент времени нулю. Следовательно, мгновенная ось вращения конуса 1 совпадает с образующей ОА.

2.1. Угол нутации , поскольку с конца оси нутации ОЕ поворот от оси прецессии OY к оси ротации Oy кажется против часовой стрелки; .

2.2. Траекторией точки С, с одной стороны, является окружность, плоскость которой перпендикулярна мгновенной оси вращения и центр которой лежит на , с другой стороны, – окружность, плоскость которой перпендикулярна оси прецессии ОY и центр которой лежит на этой оси.

Установив положение мгновенной оси вращения, найдем модуль мгновенной угловой скорости конуса. Поскольку

(I)

где – кратчайшее расстояние от точки С до мгновенной оси ;

, то

3, . Учитывая заданное направление вектора , , отложим от точки О вдоль мгновенной оси = ОА вектор так, чтобы видеть с его конца вращение конуса вокруг этой оси в направлении, противоположном направлению движения часовой стрелки (рис. 4.3.6).

С другой стороны, поскольку центр С основания конуса 1 движется по окружности, расположенной в горизонтальной плоскости, то

(II)

где – кратчайшее расстояние от точки С до оси ОY, равное .

Отсюда находим величину угловой скорости прецессии :

.

Направление вектора определим в зависимости от задания движения конуса 1, в данном случае вращение конуса 1 вокруг оси прецессии происходит по часовой стрелке, поэтому  (оси прецессии).

2.3. Векторное равенство , в котором линии действия всех его составляющих известны, позволяет определить как направление векторов всех составляющих угловых скоростей, так и величину угловой скорости ротации, а именно: ; линией действия вектора является мгновенная ось вращения ; линией действия вектора   ось прецессии OY, линией действия вектора  ось ротации Оy (рис. 4.6). Таким образом, величина угловой скорости ротации

.

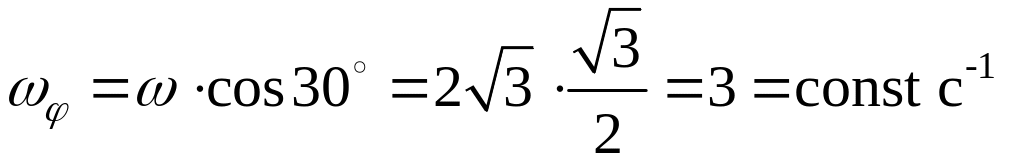2.4. Угловое ускорение в случае регулярной прецессии определяется векторным произведением , т.е. вектор  , так как с конца оси OZ поворот от вектора к вектору кажется по ходу часовой стрелки; величина углового ускорения

рад/с² .

2.5. Скорости точек конуса 1:

2.5.1) точка А , так как в данный момент времени эта точка принадлежит мгновенной оси вращения конуса 1;

2.5.2)точка В , где , и вектор  .

2.6. Ускорение какой-либо точки конуса 1 определим как геометрическую сумму осестремительного и вращательного ускорений.

2.6.1) точки А: ; ; ;

; ,

где ; м.

Вектор направлен перпендикулярно плоскости, в которой лежат векторы и , т.е. перпендикулярно ОА в сторону .

Таким образом, ; .

2.6.2) точка В: ; ;

Вектор направлен от точки B к мгновенной оси вращения конуса 1 (рис. 4 3.6). Вектор перпендикулярен плоскости, в которой лежат векторы и , принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОB в сторону . Величины этих векторов: ; , где м.

Полное ускорение точки B найдем как диагональ прямоугольника, построенного на векторах :

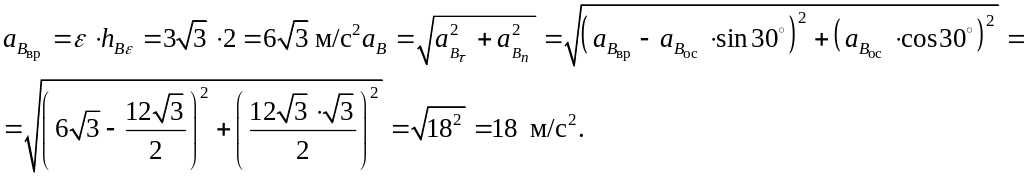2.6.3) точка С:

I) ; ; ;

.

Вектор направлен от точки С по радиусу к мгновенной оси вращения кoнуса 1.

Вектор перпендикулярен плоскости, в которой лежат векторы и , принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОС в сторону (рис. 4.3.6);

II) ;

Ответ. 1. Угол нутации  = /2; угловая скорость нутации ; прецессии 1/с; ротации 1/с; мгновенная угловая скорость 1/с.

2. Угловое ускорение конуса 1/с².

3. Скорости точек А и В  м/с. 4.Ускорения точек А, В, С /c²;

осестремительное ускорение точки С : м/с²;

вращательное ускорение точки С :  м/с².

Пример 3 выполнения расчетно-графической работы К3

Дано. Конус 1 с углом 2 при вершине катится без скольжения по неподвижному конусу 2 с углом 2 при вершине в направлении, указанном стрелкой (рис.4.3.7). Высота конуса OC = h. Вращательное ускорение центра С основания конуса =0,48 м/с², h=0,12 м, 2α = 120°,

2β = 60°.

Определить. 1. Угол нутации , угловую скорость нутации , прецессии , ротации и мгновенную угловую скорость . 2. Угловое ускорение конуса . 3. Скорости точек А, В, С: 4. Ускорения точек А, В, С: .

Решение. Введем неподвижную систему координат OXYZ с началом в точке О конуса 1. Поскольку конус 1 катится по неподвижному конусу 2 без скольжения, то скорости всех его точек, лежащих на образующей ОА, равны в данный момент времени нулю. Следовательно, мгновенная ось вращения конус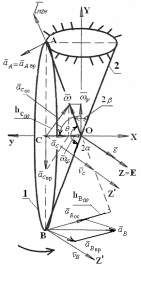 а 1 совпадает с образующей ОА.

3.1.Угол нутации: , так как с конца оси нутации ОZ=OE поворот от оси прецессии OY к оси ротации Оy кажется против часовой стрелки, .

Рис.4.3.7

3.2. Направление вектора определяется в зависимости от задания движения конуса 1 вокруг оси прецессии OY, в данном случае – против часовой стрелки, поэтому ↑↑ .

3.3. Векторное равенство , в котором линии действия всех его составляющих известны, позволяет определить как направление векторов всех составляющих угловых скоростей, так и величины угловых скоростей прецессии и ротации через мгновенную угловую скорость вращения . Так как линия действия вектора – ось прецессии OY, причем ↑↑ , линией действия вектора является мгновенная ось вращения ; линией действия вектора – ось ротации Оy, то из векторного равенства следует, что ↑↑ , а ↑↑ , а величины угловых скоростей прецессии и ротации равны 1/с = const, 1/с = const.

3.4.Угловое ускорение в случае регулярной прецессии определяется векторным произведением , т.е. вектор  , так как с конца оси OZ поворот вектора к вектору кажется против хода часовой стрелки; величина углового ускорения

1/с² .

С другой стороны, по условию задачи , где, , находим величину углового ускорения 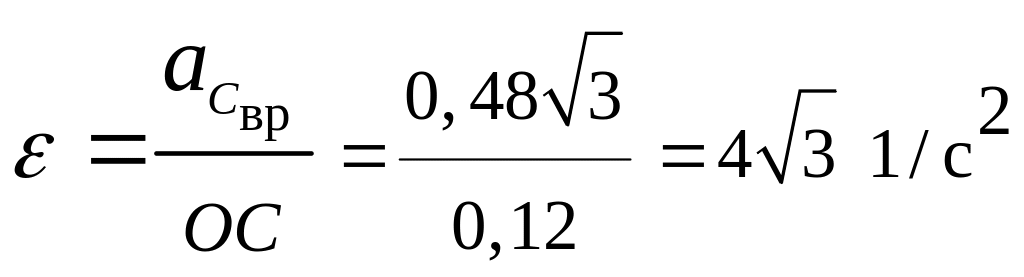. Направление вектора указано в условии. Вектор лежит в плоскости (ВОА), перпендикулярен плоскости, в которой лежат векторы и , принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОС в сторону .

Таким образом, используя полученные равенства , , , находим величины 1/с, 1/с,  1/с.

3.5. Скорости точек конуса 1:

3.5.1)точка А: , так как в данный момент времени эта точка принадлежит мгновенной оси вращения конуса 1;

3.5.2) точка В: , где (рис. 4.7), и вектор  ;

3.5.3) точка С. Траекторией точки С, с одной стороны, является окружность, плоскость которой перпендикулярна мгновенной оси вращения и центр которой лежит на , с другой стороны, – окружность, плоскость которой перпендикулярна оси прецессии ОY и центр которой лежит на этой оси. Поэтому скорость точки С конуса 1 можно определить по двум формулам:

I) , где – кратчайшее расстояние от точки С до мгновенной оси вращения , ; ,  .

С другой стороны, поскольку точка С  центр основания конуса 1 движется по окружности, расположенной в горизонтальной плоскости, то

II) , где – кратчайшее расстояние от точки С до оси ОY , ; = .

3.6. Ускорение какой-либо точки конуса 1 определим как геометрическую сумму осестремительного и вращательного ускорений.

3.6.1) точка А:

а) ; ; ;

так   как ;

;

.

Вектор направлен перпендикулярно плоскости, в которой лежат векторы и , т.е. перпендикулярно ОА в сторону . Таким образом, м/с².

3.6.2) точка В: ; ; .

Вектор направлен от точки B по радиусу к мгновенной оси вращения конуса 1. Вектор перпендикулярен плоскости, в которой лежат векторы и , принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОB в сторону .

.

Полное ускорение точки B найдем через его проекции на оси дополнительной системы координат , лежащей в плоскости (BOA), как

:

м/с²;

м/с².

3.6.3) точка С:

I) ; ; ;

м/с²;

.

Вектор направлен от точки С по радиусу к мгновенной оси вращения конуса. Направление вектора указано в условии задачи. Вектор направлен перпендикулярно ОС в сторону ;

II)

Так как в данной задаче для контроля правильности решения величину вектора можно получить как

м/с².

Ответ. 1. Угол нутации  = /2; угловая скорость нутации ; угловые скорости прецессии рад /с; ротации рад /с; мгновенная угловая скорость = 4 рад/с.

2. Угловое ускорение конуса рад/с².

3. Скорости точек А, В, С: =0; ;  м/с.

4. Ускорения точек А, В, С: = 0,96 м/с²; = 4,4 м/с²;

= 1,44 м/с².

5. Осестремительное ускорение точки С: = 0,96 м/с² ,

вращательное ускорение задано.