4.2.1.Формулы преобразования координат. Поворотные матрицы
Для любой точки М тела с координатами
x, y, z в подвижной системе
координат Оxyz, жестко связанной с
ним, и с ее же координатами X, Y,
Z в неподвижной системе координат
ОXYZ в соответствии
с (4.10), взаимосвязь проекций вектора
точки
на
оси двух систем координат
и
имеет вид
(4.14)
или в матричном виде
или
,
(4.15)
где
матрица, транспонированная к матрице
направляющих косинусов
,
задающей преобразование поворота от
осей неподвижной системы OXYZ (с
базисом
)
к осям подвижной системы Оxyz (с
базисом
),
неизменно связанной с телом.
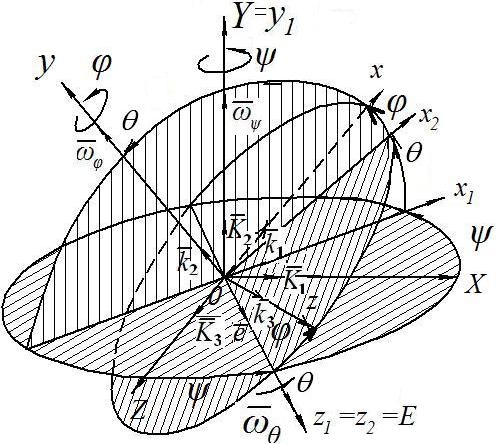
Рис.4.14.
Транспонированная матрица получается путем замены в матрице строк на столбцы. Выражение находим из формул преобразований координат при переходе от одной системы к другой:
,
(4.16)
из которых две системы
и
промежуточные.
1 Переход
от осей системы OXYZ
к осям системы
осуществляется поворотом на угол
прецессии
вокруг второй из координатных
осей (неподвижной)
–
оси прецессии системы
,
причем
.
2 Переход
от осей системы
к
осям системы
осуществляется поворотом на угол
нутации θ вокруг третьей
из координатных осей оси
-
оси нутации системы
,
причем
.
а б в
Рис.4.15
3 Переход
от осей системы
к осям системы
осуществляется поворотом на угол
ротации (собственного вращения)
вокруг второй из координатных
осей оси
системы
,
причем
.
Формулы преобразования координат получаем, рассмотрев переход от системы ОXYZ ( ) к системе Оxyz ( ), выполненный с помощью трех поворотов:
1 Первый
поворот системы ОXYZ
вокруг второй из координатных осей ОY
оси прецессии на угол прецессии
,
в результате чего получим систему
,
причем
(рис. 4.12;4.15.а; 4.16; 4.17).
1.1) Формулы преобразования координат от ОXYZ ( ) к связаны соотношениями (рис.4.16.)
X = x1 cos + 0 + z1 sin ,
Y = 0 + y1 + 0 , (4.17)
Z = x1 sin + 0 + z1 cos .
Рис.4.16.
1.2) Формулы преобразования координат от ОXYZ к в матричной форме (рис.4.17):
или
, (4.18)
где поворотная матрица
(4.19)
описывает поворот вокруг второй из
координатных осей – неподвижной оси
ОY на угол прецессии
ψ. Следует отметить, что по
структуре поворотная матрица
совершенно аналогична матрице
(4.9),
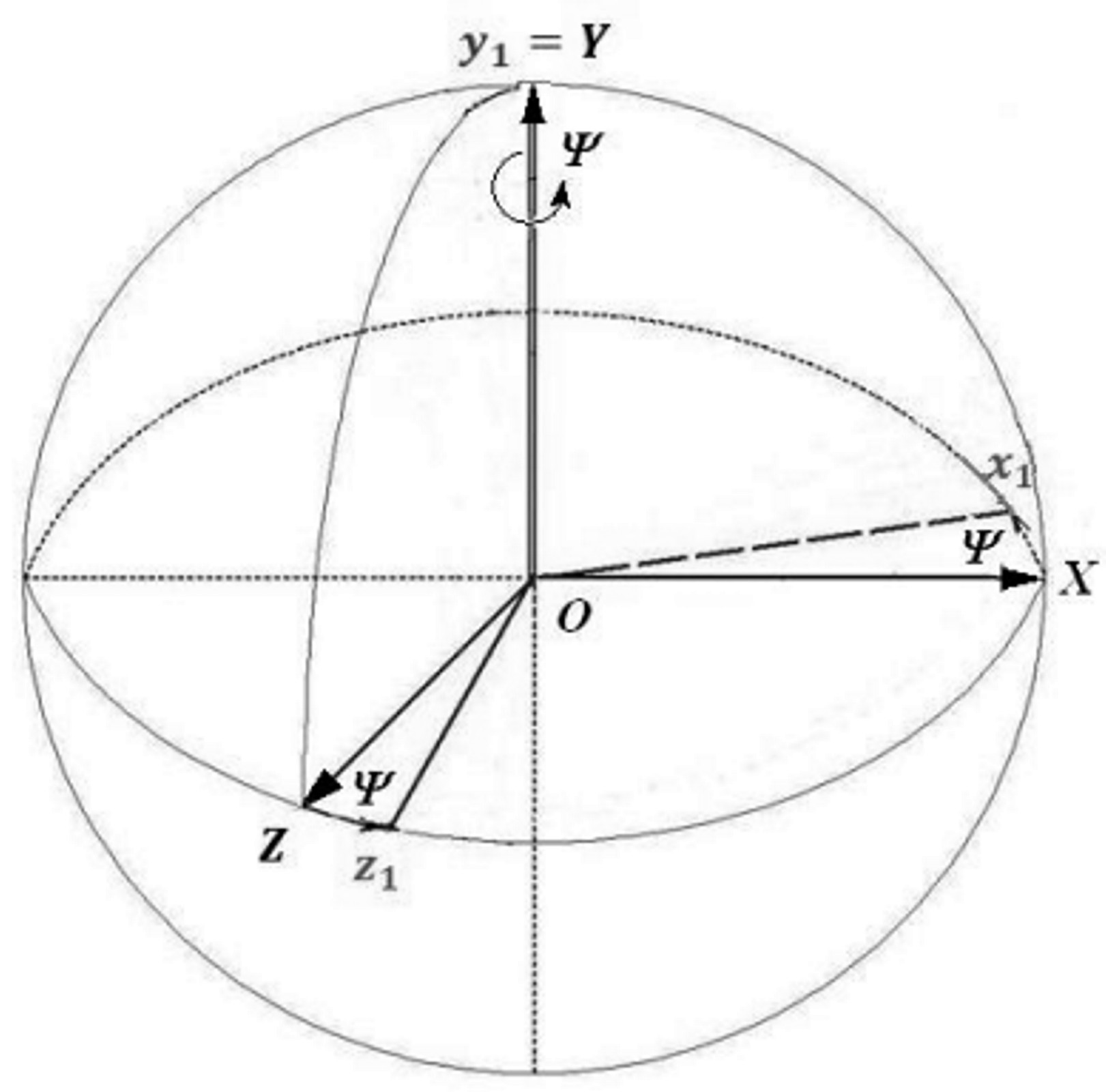
Рис.4.17.
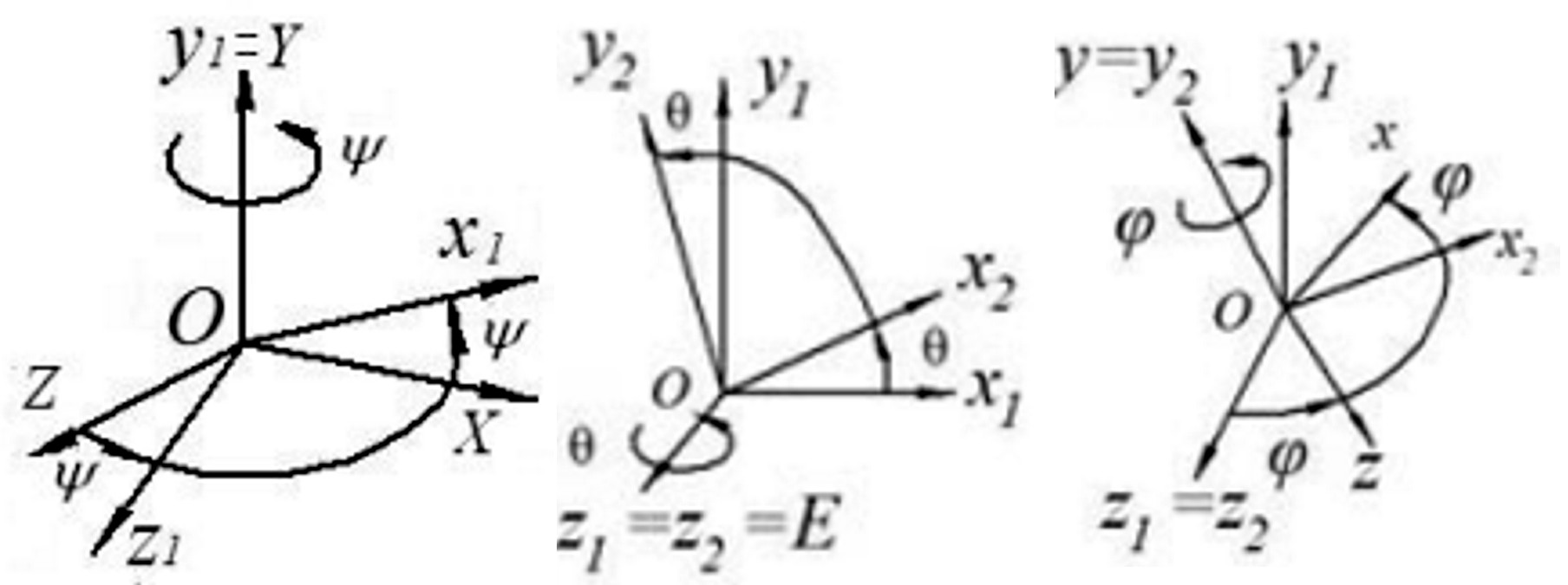
2
Второй поворот системы
вокруг третьей из координатных
осей оси нутации
на угол нутации
,
т.е.
,
при этом
(рис. 4.18; 4.19).
2.1) Формулы преобразования координат
от
к
, как видно из рис. 4.18, связаны следующими
соотношениями:
x1 = x2 cos y2 sin + 0,
y1 = x2 sin + y2 cos + 0, (4.20)
z1 = 0 + 0 + z 2,
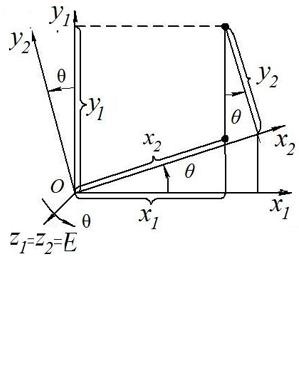Рис.4.18.
2.2) Формулы преобразования координат от к в матричной форме (рис.4.19):
или
, (4.21)
где поворотная матрица
(4.22)
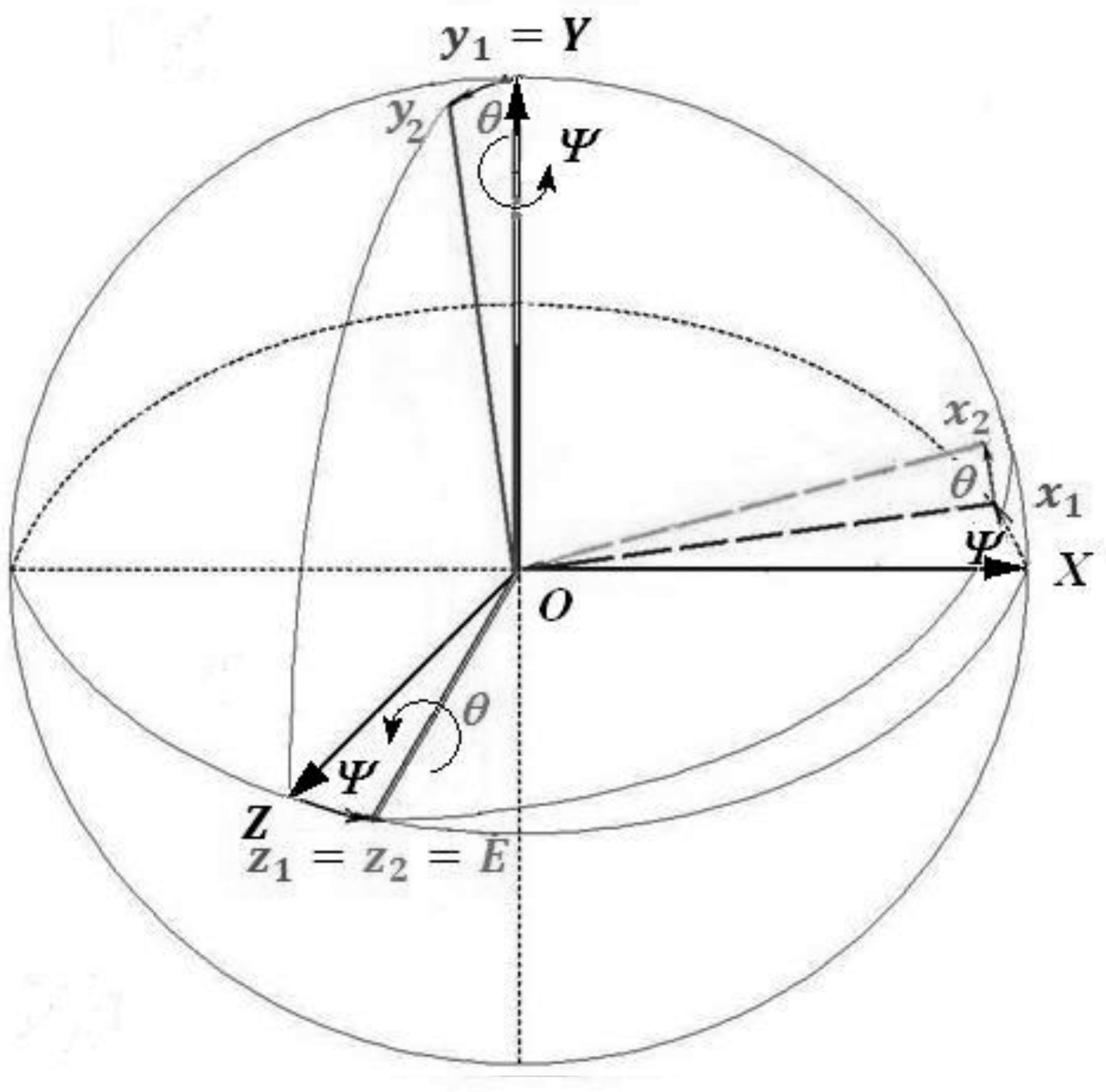
Рис. 4.19.
описывает поворот вокруг третьей
из координатных осей – оси
на угол нутации
,
при этом
.
Следует отметить, что по структуре
поворотная матрица
совершенно аналогична матрице
(4.3).
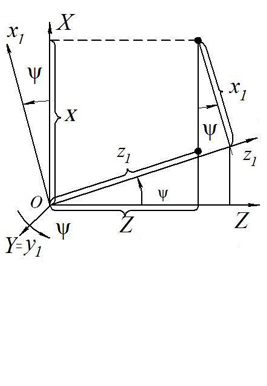
3
Третий поворот системы
вокруг опять второй из координатных
осей оси ротации
на угол
ротации (собственного вращения),
т.е.
,
при этом
(рис. 4.15,в; 4.20).
3.1) Формулы преобразования координат от к , как видно из рис. 4.15,в, связаны следующими соотношениями:
(4.23)
3.1) Формулы преобразования координат от к в матричной форме: (рис.4.12; 4.20 *)
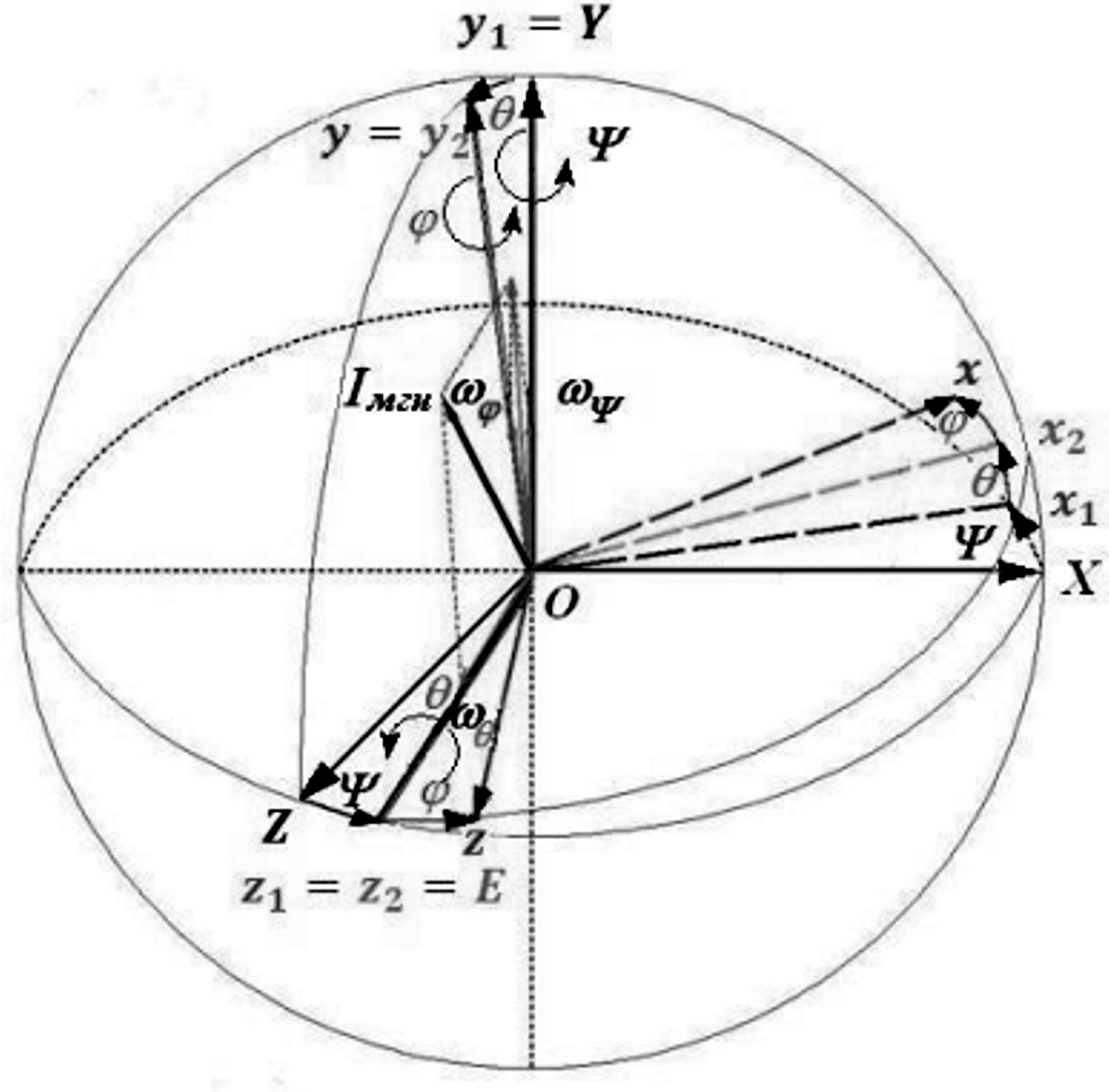
Рис.4.20*
или
,
(4.24)
где поворотная матрица
(4.25)
описывает поворот вокруг опять второй из координатных осей – оси ротации на угол ротации (собственного вращения), т.е. , при этом (рис. 4.15,в; 4.20). . Следует отметить, что по структуре поворотная матрица (4.25) аналогична матрице (4.19).
Подставляя в (4.8) соотношение (4.21), получаем промежуточную формулу преобразования координат, которая может понадобиться в дальнейшем
,
(4.26)
где промежуточная поворотная матрица
находится
как произведение двух матриц поворота,
=
(4.27)
Подставляя в (4.8) формулы (4.21) и (4.24), получаем
(4.28)
Сравнивая выражения (4.15) и (4.2), находим, что искомая поворотная матрица является произведением трех матриц поворота (4.19), (4.22), (4.25):
или (4.29)
При заданном законе сферического движения выражения (4.15) и (4.29) позволяют определить искомый закон движения и траекторию выбранной точки твердого тела.