4.2. Углы Эйлера

В тех случаях, когда угловая скорость вращения твердого тела в одном направлении значительно больше, чем в двух других (генераторы,

Рис.4.10

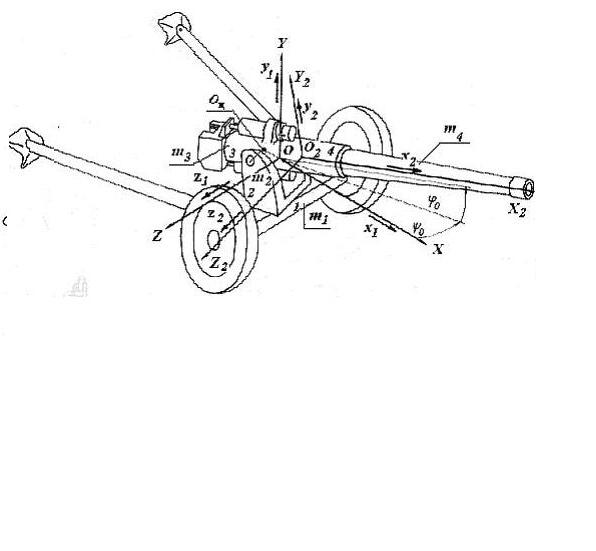
Рис.4.11

моторы, турбины, гироскопы, снаряды), для определения положения тела в качестве трех независимых параметров выбирают три угла Эйлера: угол прецессии  (t), угол нутации  (t) и угол ротации (собственного вращения)  (t). Их названия заимствованы из астрономии.

Чтобы задать эти углы, рассмотрим вращение твердого тела вокруг неподвижной точки О. Пусть даны некоторая система отсчета и связанная с ней неподвижная система координат ОXYZ, относительно которой движется твердое тело, и связанная с твердым телом система координат

Оxyz, которая движется относительно первой (рис.4.10 4.13). Это означает, что первая и вторая системы координат имеют общее начало O. Так, рассматривая кинематику частей лафета орудия (рис.4.11), за начало выбирают точку О пересечения оси вращения боевого штыря с горизонтальной плоскостью, перпендикулярной плоскости симметрии орудия, на

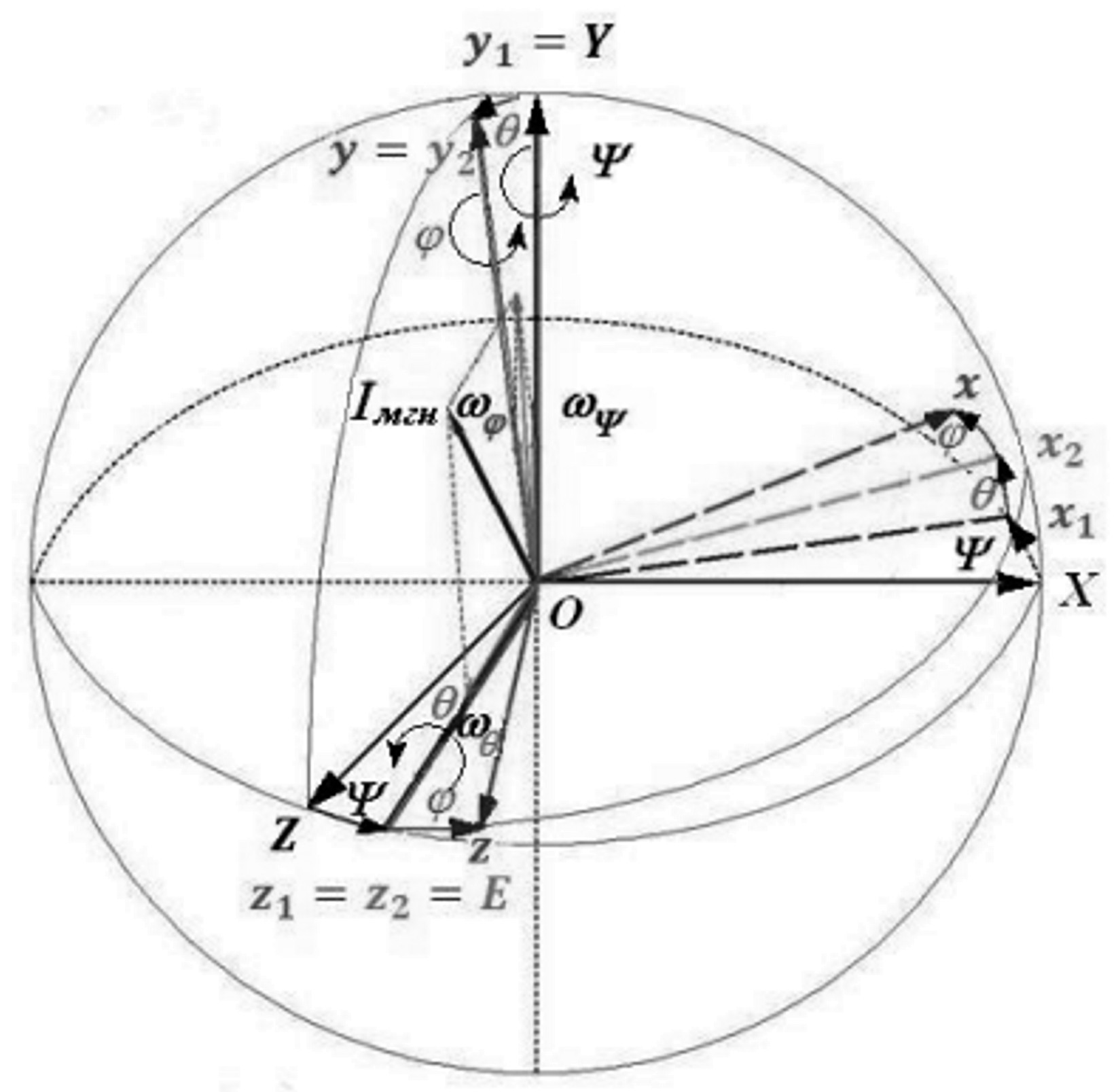
Рис.4.12

высоте оси цапф до выстрела. Ось ОX –направляем горизонтально, ее ориентацию целесообразно связывать с направлением полета снаряда, когда плоскость стрельбы совпадает с плоскостью симметрии орудия, т.е. это продольная ось в плоскости симметрии (ракеты, орудия, танка при нулевом угле возвышения); ось OY- будет ориентировать вертикально положительное направление вверх. Ось OZ –вправо для наблюдателя, смотрящего вдоль оси ОX. (рис.4.10, рис.4.12). Углы, образуемые осями Оxyz с осями ОXYZ, изменяются, т.е. система Оxyz поворачивается вместе с твердым телом вокруг неподвижной точки О (рис.4.10, рис.4.12).

П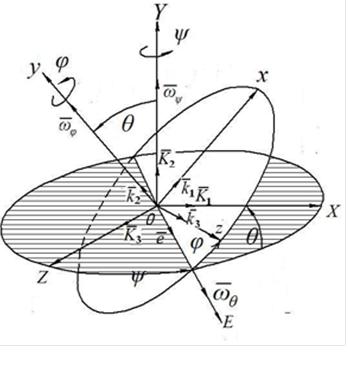 лоскость ОXZ (заштрихованный овал) пересекает плоскость Оxz (белый овал) по некоторой (рис.4.13) прямой Оz₁ =Оz₂ = OE, образующей угол с неподвижной осью ОZ, и угол с подвижной осью Оz, которая называется «линией узлов» ОЕ с единичным ортом .

Рис.4.13

Кроме того, плоскость Оxz образует с плоскостью ОXZ угол , равный углу между осями ОY и Оy.

Неподвижная ось ОY, вокруг которой поворачивается твердое тело на угол прецессии , называется осью прецессии с единичным ортом .

Изменение угла нутации  сопровождается вращением твердого тела вокруг линии узлов Оz₂ , называемой осью нутации с единичным ортом (рис.4.12; 4.13).

Наконец, угол ротации (собственного вращения)  характеризует вращение тела вокруг оси Oy = Oy₂, называемой осью ротации (собственного вращения) с единичным ортом .

На рис (4.10 - 4.13) все углы положительные, т.е. против хода часовой стрелки, если смотреть на поворот тела с положительных направлений осей вращения OY, OE и O y.

Движение твердого тела в любой момент времени полностью определяется положением подвижной связанной с твердым телом системы координат Оxyz относительно неподвижной системы координат ОXYZ, т.е. заданием кинематических уравнений вращения тела вокруг неподвижной точки О: угла прецессии , угла нутации и угла ротации (собственного вращении).