
- •Кинематика
- •Кинематика точки
- •Способы задания движения точки
- •Векторный способ задания движения точки
- •Координатный способ задания движения точки
- •Частный случай задания движения точки в полярной системе координат
- •1.1.3. Траекторный (естественный) способ задания движения точки
- •Определение пути s(t), пройденного точкой по траектории
- •Скорость точки при различных способах задания ее движения
- •1.2.1. Скорость точки при векторном способе задания ее движения
- •1.2.2. Скорость точки при координатном способе задания ее движения
- •1.2.3 Скорость точки при траекторном способе задания ее движения
- •1.3.2. Ускорение точки при координатном способе задания ее движения
- •Понятие о сопровождающем (естественном) трехграннике
- •1.3.3. Ускорение точки при естественном способе задания ее движения
- •Кинематические уравнения движения точки по траектории (закон скоростей и закон траекторных координат)
- •Способы задания движения точки и кинематические характеристики
- •Расчетно-графическая работа к 1 Кинематика точки
- •Простейшие движения твердого тела
- •2.1. Степени свободы
- •2.2. Поступательное движение твердого тела
- •2.3. Вращение твердого тела вокруг неподвижной оси
- •2.3.1 Угловая скорость и угловое ускорение тела
- •2.3.2 Скорость и ускорение любой точки твердого тела при его вращении вокруг неподвижной оси
- •Плоское движение твердого тела
- •3.1. Уравнения движения, угловая скорость и угловое ускорение твердого тела при плоском движении
- •3.2. Скорости точек твердого тела при плоском движении
- •3.2.1. Метод полюса
- •3.2.2. Метод мгновенного центра скоростей
- •3.2.3. Определение положения мгновенного центра скоростей
- •3.4. Расчетно-графическая работа к2 Кинематика плоского движения
- •3.4.1. Схемы конструкций и исходные данные
- •Продолжение табл.3.4.1
- •Окончание табл. 3.1.1
- •3.4.2. Указания и план выполнения
- •3.4.3. Пример выполнения расчетно-графической работы к2 Кинематика плоского движения
- •4.2. Углы Эйлера
- •4.2.1.Формулы преобразования координат. Поворотные матрицы
- •4.2.2. Мгновенная угловая скорость и угловое ускорение. Кинематические уравнения Эйлера
- •4.2.3. Скорость и ускорение точек тела. Формула Ривальса
- •4.3. Расчетно-графическая работа к3 Кинематика вращательного движения твердого тела вокруг неподвижной точки (случай регулярной прецессии).
- •4.3.1.Схемы конструкций и исходные данные
- •4.3.2. Указания и план выполнения
- •4.3.3. Примеры выполнения расчетно-графической работы к3 (регулярная прецессия)
- •4.4. Общий случай движения твердого тела
- •6. Сложное движение точки
- •6.1. Относительное, переносное и абсолютное движения точки
- •6.2. Зависимости между скоростями и ускорениями точек в относительном, переносном и абсолютном движениях
- •6.3. Расчетно-графическая работа к4 Кинематика сложного движения точки при переносном вращательном движении
- •6.3.1. Схемы конструкций и исходные данные
- •6.3.2. Указания и план выполнения
- •6.3.3. Пример выполнения расчетно-графической работы к4 сложное движение точки при переносном вращательном движении
- •1. Кинематические характеристики точки м в относительном движении
- •2. Кинематические характеристики точки м в переносном вращательном движении
- •Литература Основная
- •Дополнительная
- •Образец оформления титульного листа
- •Кинематика Расчетно-графическая (курсовая) работа
- •1. Кинематика точки……………………………………………..2
- •1.1. Способы задания движения точки…………………………………3
- •1.4. Кинематические уравнения движения точки по траектории (закон скоростей и закон траекторных координат) ……………15
- •6.2. Зависимости между скоростями и ускорениями точек в относительном, переносном и абсолютном движениях……
3.2.3. Определение положения мгновенного центра скоростей
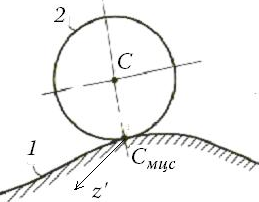
1.Положение МЦС плоской фигуры в некоторых случаях, исходя из
ф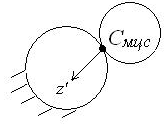 изических
соображений, удается сразу определить,
когда например, качение без скольжения
колеса по неподвижной прямой (рис.
3.6.1,а) или колеса по другому неподвижному
колесу (рис. 3.6.1,б).
изических
соображений, удается сразу определить,
когда например, качение без скольжения
колеса по неподвижной прямой (рис.
3.6.1,а) или колеса по другому неподвижному
колесу (рис. 3.6.1,б).
 а Рис.
3.6.1 б
а Рис.
3.6.1 б
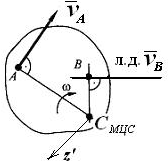 2.Положение
МЦС может быть установлено с помощью
геометрических построений. Если известны
линии действия скоростей двух точек
А и В фигуры (рис.3.6.2) и они не
параллельны, то МЦС находится в точке
2.Положение
МЦС может быть установлено с помощью
геометрических построений. Если известны
линии действия скоростей двух точек
А и В фигуры (рис.3.6.2) и они не
параллельны, то МЦС находится в точке
Рис.3.6.2
п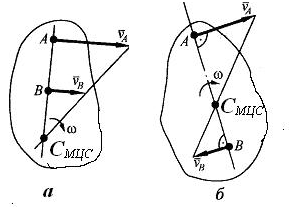 ересечения
перпендикуляров к линиям действия
скоростей двух точек А и В
ересечения
перпендикуляров к линиям действия
скоростей двух точек А и В
![]() ,
восстановленных из этих точек.
,
восстановленных из этих точек.
Рис.3.6.3.
3.Если точки А и В фигуры лежат на общем перпендикуляре и линии
действия скоростей этих точек параллельны
![]() (рис.3.6.3,а), или
(рис.3.6.3,а), или
![]() (рис.3.6.3,б), но по модулю не равны, то МЦС
находится в точке пересечения
перпендикуляра с прямой, соединяющей
концы векторов скоростей этих точек.
(рис.3.6.3,б), но по модулю не равны, то МЦС
находится в точке пересечения
перпендикуляра с прямой, соединяющей
концы векторов скоростей этих точек.
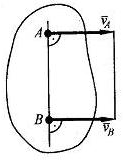 Рис.3.6.4.
Рис.3.6.4.
4. Если скорости двух точек А и В
плоской фигуры параллельны,
направлены в одну сторону
и равны между собой
![]() (рис.3.6.4) , то МЦС лежит в бесконечности,
а угловая скорость плоской фигуры равна
нулю
(рис.3.6.4) , то МЦС лежит в бесконечности,
а угловая скорость плоской фигуры равна
нулю
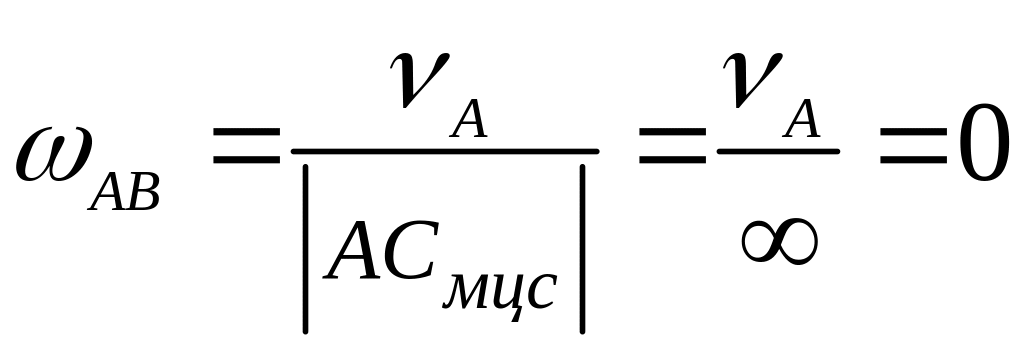 ,
так как
,
так как
![]() ,
то.
,
то.
![]() .
.
Такое движение тела называют случаем мгновенно-поступательного движения. При этом скорости всех точек плоской фигуры одинаковы как по направлению, так и по модулю. Однако ускорения точек будут различны.
Пример 3.1. Колесо радиуса R (рис. 3.7) катится без скольжения по
неподвижной прямой; скорость центра
![]() .
Определить скорости точек A
и B обода
колеса методом мгновенного центра
скоростей МЦС.
.
Определить скорости точек A
и B обода
колеса методом мгновенного центра
скоростей МЦС.
Решение. Поскольку колесо
катится без скольжения, то точка
находится в точке контакта обода с
неподвижной прямой. Тогда, в соответствии
с (3.7), угловая скорость колеса
![]() ,
а направление его вращения
определяется направлением вектора
относительно оси
z’
(
,
а направление его вращения
определяется направлением вектора
относительно оси
z’
(![]() ,
т.е. по ходу часовой стрелки). Поскольку
мгновенные радиусы ВСмцс=
,
т.е. по ходу часовой стрелки). Поскольку
мгновенные радиусы ВСмцс=![]() и АСмцс = 2R,
то
и АСмцс = 2R,
то
![]() Векторы
ско
Векторы
ско
ростей точек B и A обода колеса перпендикулярны мгновенным радиусам и направлены в сторону вращения колеса вокруг z’.
 Рис.3.7
Рис.3.7
3.3.Ускорения точек тела при плоском движении методом полюса
Самый рациональный способ при определении ускорений точек плоской фигуры метод полюса. В разд.3.2.1 было получено соотношение
(3.4) между скоростями двух точек плоской фигуры методом полюса
(за полюс принята точка P)
Продифференцировав его по времени,
получим
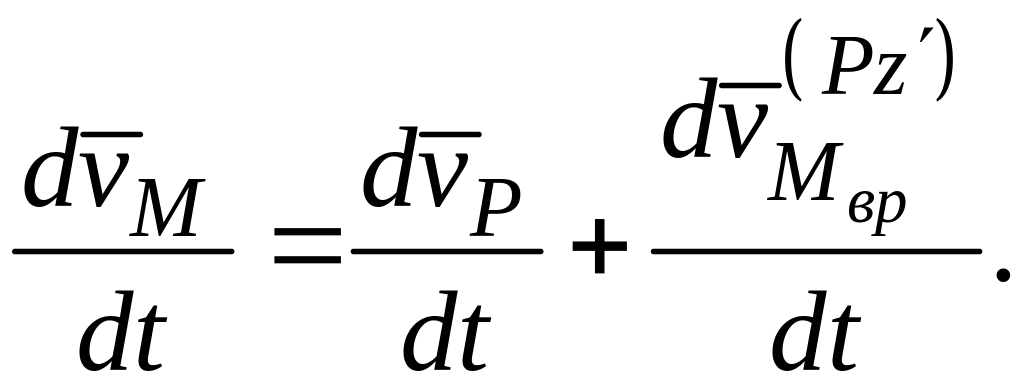
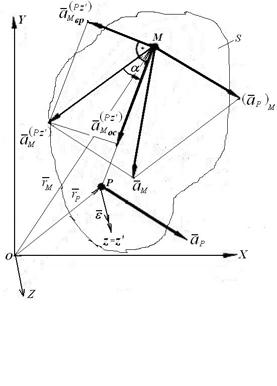
Рис.3.8
Здесь
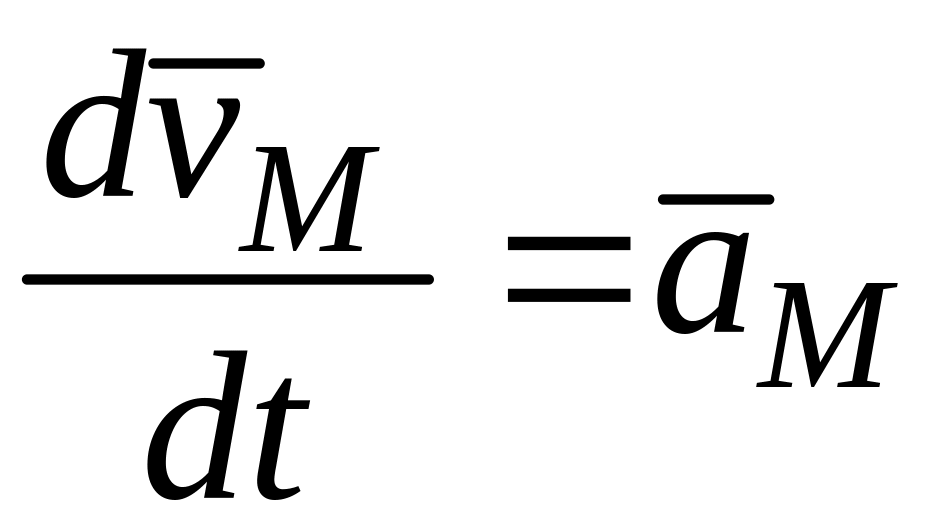 ,
,
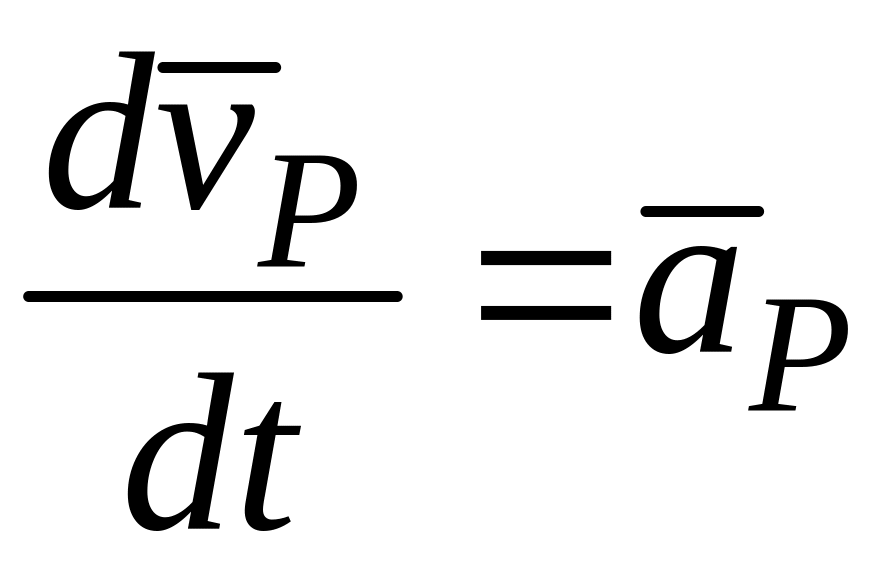
ускорения точек P и M
относительно неподвижной системы
координат;
ускорения точек P и M
относительно неподвижной системы
координат;
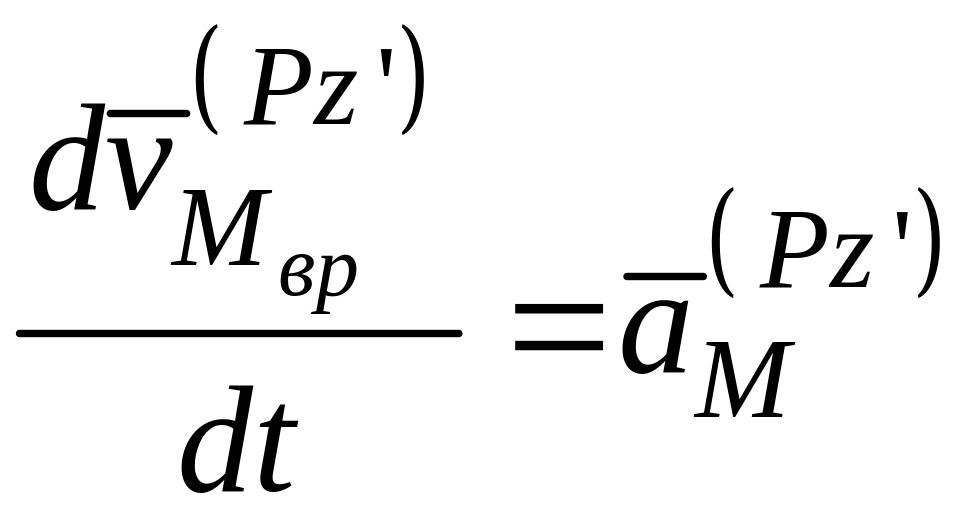
ускорение точки M при
вращательном движении плоской фигуры
вокруг подвижной оси z’,
проходящей через полюс P
P
z’ перпендикулярно
плоскости плоской фигуры, или просто
вокруг полюса P.
Таким образом,
ускорение точки M при
вращательном движении плоской фигуры
вокруг подвижной оси z’,
проходящей через полюс P
P
z’ перпендикулярно
плоскости плоской фигуры, или просто
вокруг полюса P.
Таким образом,
![]() ,
(3.8)
,
(3.8)
т.е. ускорение какой-либо точки
плоской фигуры при плоском движении
равно векторной сумме ускорения полюса,
построенного при рассматриваемой точке,
и ускорения этой точки при вращательном
движении плоской фигуры вокруг оси z’,
проходящей через полюс![]() ,
перпендикулярно плоскости плоской
фигуры.
,
перпендикулярно плоскости плоской
фигуры.
Ускорение точки
![]() при вращательном движении плоской
фигуры вокруг оси Pz’,
как и в случае вращения тела вокруг
неподвижной оси, состоит из вращательной
касательной
(тангенциальной)
при вращательном движении плоской
фигуры вокруг оси Pz’,
как и в случае вращения тела вокруг
неподвижной оси, состоит из вращательной
касательной
(тангенциальной)
![]() (3.9)
(3.9)
и осестремительной нормальной составляющих:
![]() , (3.10)
, (3.10)
величины которых
![]()
![]() (3.11)
(3.11)
Вращательное
касательное ускорение
![]() направлено
перпендикулярно отрезку PM
в сторону
(рис.3.8).
направлено
перпендикулярно отрезку PM
в сторону
(рис.3.8).
Осестремительное
нормальное
![]() направлено
от точки M по
радиусу PM к оси
вращения
.
Таким образом,
направлено
от точки M по
радиусу PM к оси
вращения
.
Таким образом,
![]() =
=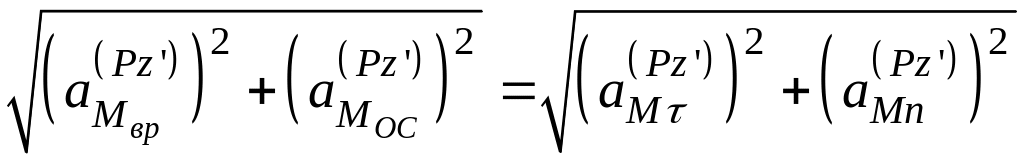 =
=
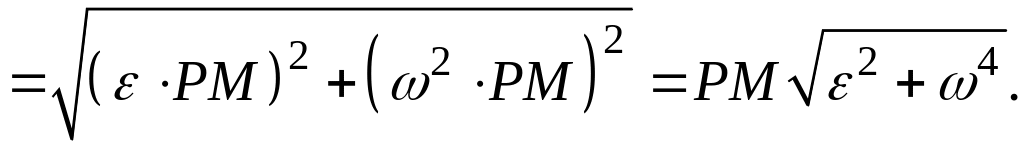 (3.12)
(3.12)
Обозначив угол между ускорением
и
отрезком PM через
![]() ,
,
найдем 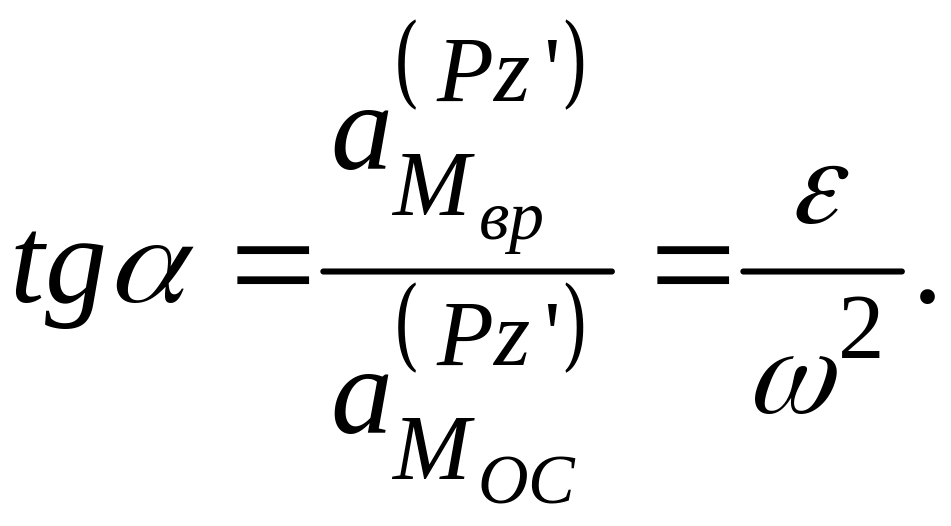 (3.13)
(3.13)
Пример 3.2. Центр колеса
радиуса R, катящегося
без скольжения по неподвижной прямой
(рис.3.9) движется в данный момент времени,
имея ускорение
![]() .
Угловая скорость и угловое ускорение
колеса
,
.
.
Угловая скорость и угловое ускорение
колеса
,
.
О пределить:
ускорения точек А, В и
,
расположенных на концах
вертикального и горизонтального
диаметров обода колеса.
пределить:
ускорения точек А, В и
,
расположенных на концах
вертикального и горизонтального
диаметров обода колеса.
Рис.3.9
Решение. За полюс примем точку С, ускорение которой задано. Тогда,
согласно (3.8 3.10), ускорение точки А
![]() ,
где
,
где
![]() =
=
![]() =
=
![]() ;
;
![]() =
=
![]() =
=![]() .
.
Ускорение
![]() перпендикулярно
отрезку СА и направлено в сторону
углового ускорения
;
а ускорение
перпендикулярно
отрезку СА и направлено в сторону
углового ускорения
;
а ускорение
![]() направлено от точки А к полюсу С.
Составляющие искомого вектора
направлено от точки А к полюсу С.
Составляющие искомого вектора
![]() показаны на (рис.3.9). Его величина
показаны на (рис.3.9). Его величина
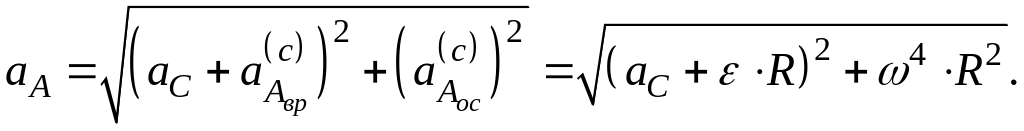
Аналогично рассуждая, находим ускорения для точек В и
соответственно:
![]() =
=
![]() ;
; ![]() =
=![]() ;
;
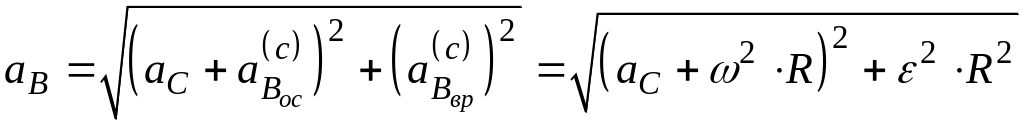 и
и
![]() =
=
![]() ;
; ![]() =
=![]() ;
;
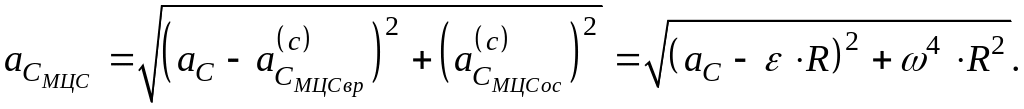
Таким образом, ускорение точки
колеса при его качении по неподвижному
основанию не может быть равно нулю,
поскольку осе-стремительная
нормальная составляющая ускорения
=![]() имеет не нулевое значение.
имеет не нулевое значение.
Пример 3.3. Определить
угловое ускорение
![]() линейки АВ эллипсографа (рис.3.10),
если заданы ее угловая скорость
линейки АВ эллипсографа (рис.3.10),
если заданы ее угловая скорость
![]() и ускорение шарнира С кривошипа ОС
и ускорение шарнира С кривошипа ОС
![]() .
Заданы также размеры звеньев и положение
механизма в рассматриваемый момент
времени.
.
Заданы также размеры звеньев и положение
механизма в рассматриваемый момент
времени.
Решение. За полюс линейки АВ примем шарнир С, ускорение которого задано. Тогда, согласно (3.8 3.10),
![]() .
(3.14*)
.
(3.14*)
В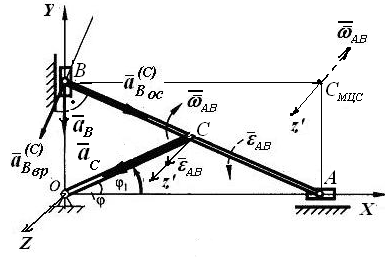 этом векторном уравнении векторы
этом векторном уравнении векторы
![]() и
и
![]() известны по мо
известны по мо
Рис.3.10
дулю и направлению: (![]() задано
условием задачи, а
задано
условием задачи, а
![]()
направлен от точки В к полюсу С).
Что касается векторов
![]() и
и
![]() ,
величины их не известны, известны лишь
их линии действия: (рис.3.10), а именно:
,
величины их не известны, известны лишь
их линии действия: (рис.3.10), а именно:
(
перпендикулярен
ВС, а линия действия
-
ось OY). Такое векторное
уравнение (3,14*) решается методом
проецирования на такие оси координат,
например, 1на
ось ОХ, перпендикулярную неизвестному
вектору
,
тогда находим величину вектора
,
которая должна быть положительной,
т.е.
![]() >
0 ,
>
0 ,
2 на ось OY,
находим величину вектора
,
которая должна быть положительной, т.е.
![]() >0,
тогда направление вектора
выбрано верно.
>0,
тогда направление вектора
выбрано верно.
1 Проекция векторное
уравнения (3,14*) на ось OX,
полагая, что угловое ускорение линейки![]() ,
т.е. против хода часовой стрелки,
,
т.е. против хода часовой стрелки,
![]()
В этом уравнении в силу принятого
предварительно направления
проекция вектора
на ось Ox будет
отрицательная. Отсюда находим
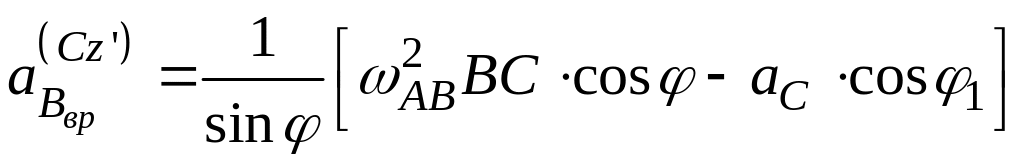 или
или
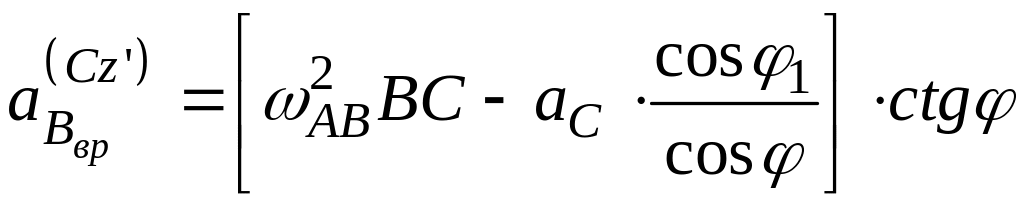 .
.
Направление углового ускорения линейки
эллипсографа определяется знаком![]() .
Если
0, то направление
.
Если
0, то направление
![]() (рис.3.10) выбрано правильно, т.е.
.
При
0, наоборот,
(рис.3.10) выбрано правильно, т.е.
.
При
0, наоборот,
![]() .
.
На рис.3.10
![]() и
и
![]() .=
0, т.к.
.=
0, т.к.
![]() ,
,
а
![]() и ОС = ВС. Таким образом
=
0 и
и ОС = ВС. Таким образом
=
0 и
![]() =
=
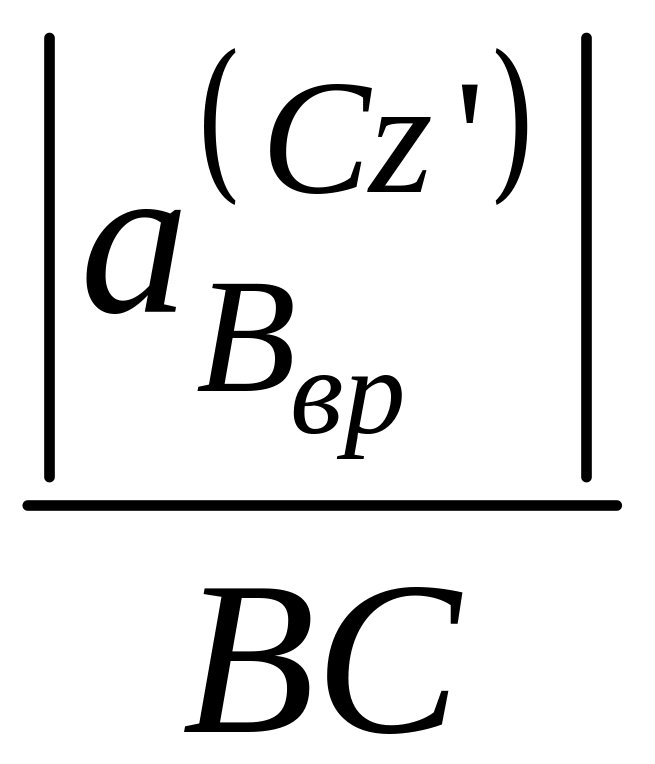 = 0
= 0
2 Проекция векторное уравнения (3,14*) на ось OY, полагая, что угловое ускорение линейки , т.е. против хода часовой стрелки,
![]()
Из последнего уравнения находим величину вектора , которая как видно из последнего уравнения положительная, т.е. >0, т.е. направление вектора выбрано верно. Но в связи с названными комментариями к п. 1), величина =0.
