
- •Кинематика
- •Кинематика точки
- •Способы задания движения точки
- •Векторный способ задания движения точки
- •Координатный способ задания движения точки
- •Частный случай задания движения точки в полярной системе координат
- •1.1.3. Траекторный (естественный) способ задания движения точки
- •Определение пути s(t), пройденного точкой по траектории
- •Скорость точки при различных способах задания ее движения
- •1.2.1. Скорость точки при векторном способе задания ее движения
- •1.2.2. Скорость точки при координатном способе задания ее движения
- •1.2.3 Скорость точки при траекторном способе задания ее движения
- •1.3.2. Ускорение точки при координатном способе задания ее движения
- •Понятие о сопровождающем (естественном) трехграннике
- •1.3.3. Ускорение точки при естественном способе задания ее движения
- •Кинематические уравнения движения точки по траектории (закон скоростей и закон траекторных координат)
- •Способы задания движения точки и кинематические характеристики
- •Расчетно-графическая работа к 1 Кинематика точки
- •Простейшие движения твердого тела
- •2.1. Степени свободы
- •2.2. Поступательное движение твердого тела
- •2.3. Вращение твердого тела вокруг неподвижной оси
- •2.3.1 Угловая скорость и угловое ускорение тела
- •2.3.2 Скорость и ускорение любой точки твердого тела при его вращении вокруг неподвижной оси
- •Плоское движение твердого тела
- •3.1. Уравнения движения, угловая скорость и угловое ускорение твердого тела при плоском движении
- •3.2. Скорости точек твердого тела при плоском движении
- •3.2.1. Метод полюса
- •3.2.2. Метод мгновенного центра скоростей
- •3.2.3. Определение положения мгновенного центра скоростей
- •3.4. Расчетно-графическая работа к2 Кинематика плоского движения
- •3.4.1. Схемы конструкций и исходные данные
- •Продолжение табл.3.4.1
- •Окончание табл. 3.1.1
- •3.4.2. Указания и план выполнения
- •3.4.3. Пример выполнения расчетно-графической работы к2 Кинематика плоского движения
- •4.2. Углы Эйлера
- •4.2.1.Формулы преобразования координат. Поворотные матрицы
- •4.2.2. Мгновенная угловая скорость и угловое ускорение. Кинематические уравнения Эйлера
- •4.2.3. Скорость и ускорение точек тела. Формула Ривальса
- •4.3. Расчетно-графическая работа к3 Кинематика вращательного движения твердого тела вокруг неподвижной точки (случай регулярной прецессии).
- •4.3.1.Схемы конструкций и исходные данные
- •4.3.2. Указания и план выполнения
- •4.3.3. Примеры выполнения расчетно-графической работы к3 (регулярная прецессия)
- •4.4. Общий случай движения твердого тела
- •6. Сложное движение точки
- •6.1. Относительное, переносное и абсолютное движения точки
- •6.2. Зависимости между скоростями и ускорениями точек в относительном, переносном и абсолютном движениях
- •6.3. Расчетно-графическая работа к4 Кинематика сложного движения точки при переносном вращательном движении
- •6.3.1. Схемы конструкций и исходные данные
- •6.3.2. Указания и план выполнения
- •6.3.3. Пример выполнения расчетно-графической работы к4 сложное движение точки при переносном вращательном движении
- •1. Кинематические характеристики точки м в относительном движении
- •2. Кинематические характеристики точки м в переносном вращательном движении
- •Литература Основная
- •Дополнительная
- •Образец оформления титульного листа
- •Кинематика Расчетно-графическая (курсовая) работа
- •1. Кинематика точки……………………………………………..2
- •1.1. Способы задания движения точки…………………………………3
- •1.4. Кинематические уравнения движения точки по траектории (закон скоростей и закон траекторных координат) ……………15
- •6.2. Зависимости между скоростями и ускорениями точек в относительном, переносном и абсолютном движениях……
2.3.2 Скорость и ускорение любой точки твердого тела при его вращении вокруг неподвижной оси
Свойством вращательного движения твердого тела считается то, что траектории всех точек этого тела являются окружностями, лежащими
Р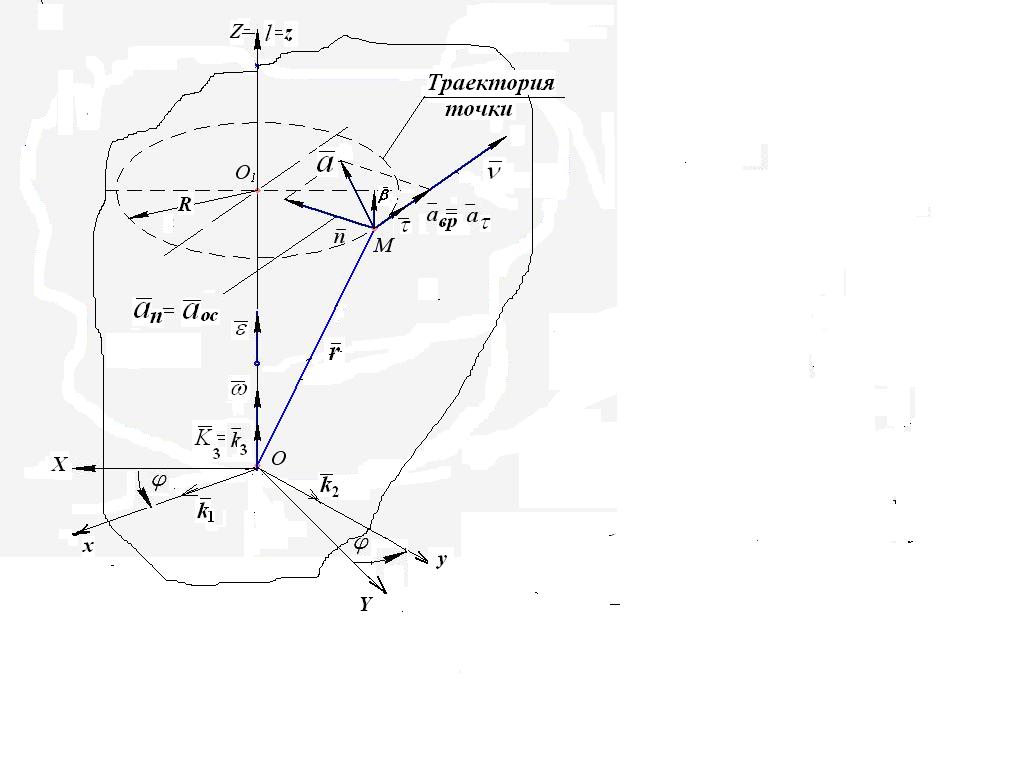 ис.2.4
ис.2.4
в плоскостях, перпендикулярных оси
вращения. Центры всех этих окруж-ностей
лежат на оси вращения, а радиусы равны
кратчайшему расстоянию от этих точек
до оси вращения. На рис.2.4 для точки M
тела, вращающегося вокруг неподвижной
оси OZ показана ее
траектория - окружность радиусом R
, а также единичные векторы![]() ,
,
![]() ,
,
![]() системы координат сопровождающего
трехгранника, причем вектор бинормали
напра-влен так же, как единичный вектор
системы координат сопровождающего
трехгранника, причем вектор бинормали
напра-влен так же, как единичный вектор
![]() на оси Oz см. (1.28):
=
[
].
на оси Oz см. (1.28):
=
[
].
Как видно из рис.2.4 и 2.5
![]() .
.
 или
или
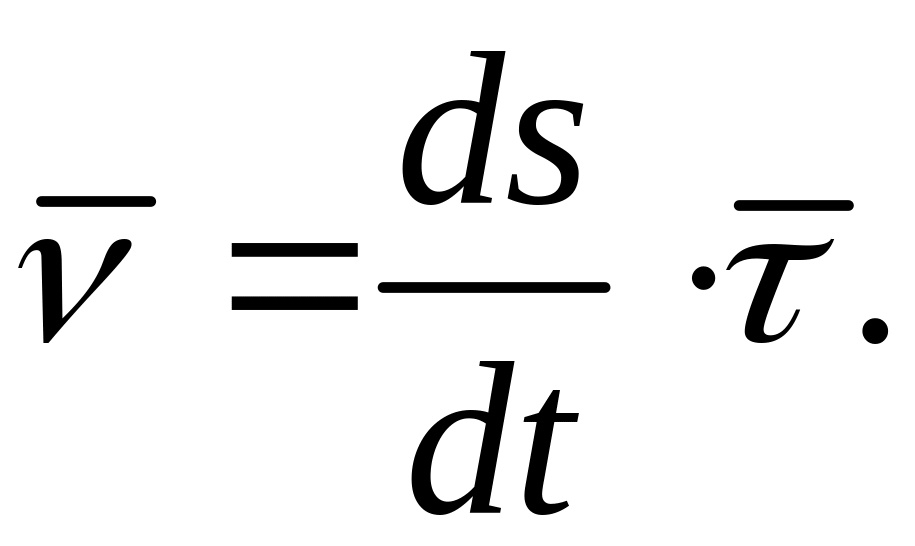
R = hz= МО1 – радиус окружности траектории точки М;
![]()
 -
траекторная координата точки М, где
= const,
-
траекторная координата точки М, где
= const,
hz = const.
Рис.2.5

 .
Таким образом
.
Таким образом
![]() (2.13)
(2.13)
Причем:
![]() если
если
![]()
![]() если
если
![]()
Скорости точек при вращении вокруг неподвижной оси направлены по касательной к окружности радиусом h = R в соответствии с направлением угловой скорости тела.
Скорость точки твердого тела можно
определить по векторной формуле
Эйлера:
![]() или
или
 .
(2.14)
.
(2.14)
Вектор скорости точки М тела, вращающегося вокруг неподвижной
оси, определяется векторным произведением вектора угловой скорости тела на радиус-вектор точки М относительно какой-либо точки О, лежащей на оси вращения тела:
Положение точки М относительно
неподвижной точки О на оси вращения
определяется с помощью радиус-вектора
![]() :
:
=
![]() где
где
![]()
причем
![]()
Направление вектора
![]() можно
также определить, исходя из свойств
векторного произведения (2.14).
можно
также определить, исходя из свойств
векторного произведения (2.14).
Численное значение (модуль) скорости точки тела при этом определяется как модуль соответствующего векторного произведения, т.е.
![]() (2.15)
(2.15)
Ускорение точки М тела

В последнем выражении
![]() вектор углового
ускорения тела, а
вектор углового
ускорения тела, а
![]() скорость точки
М (рис.2.4); поэтому
скорость точки
М (рис.2.4); поэтому
![]() (2.16)
(2.16)
Слагаемые в правой части выражения
(2.16) представляют собой вращательную
![]() и осестремительную
и осестремительную
![]() составляющие ускорения точки.
составляющие ускорения точки.
Направление
![]() ,
исходя из векторного произведения
,
исходя из векторного произведения
![]() ,
будет определено как направление
вектора, касательного к окружности
радиусом h = R
в точке М. На рис.2.4 видно, что
это направление также соответствует
направлению углового ускорения точки.
Модуль вращательного ускорения точки
в данном случае равен
,
будет определено как направление
вектора, касательного к окружности
радиусом h = R
в точке М. На рис.2.4 видно, что
это направление также соответствует
направлению углового ускорения точки.
Модуль вращательного ускорения точки
в данном случае равен
![]() (2.17)
(2.17)
Вектор
![]() всегда
направлен по нормали к траектории точки
М в сторону ее вогнутости (к оси
вращения тела). Модуль осестремительного
ускорения точки
всегда
направлен по нормали к траектории точки
М в сторону ее вогнутости (к оси
вращения тела). Модуль осестремительного
ускорения точки
![]() (2.18)
(2.18)
Таким образом, видно, что модули скоростей и ускорений точек тела, вращающегося вокруг неподвижной оси, прямо пропорциональны кратчайшему расстоянию от них до оси вращения (h=R) , причем, чем дальше находится точка от оси вращения, тем больше ее скорость и ускорения.
Следует заметить, что только для частного случая движения точки при траекторном способе задания ее движения, когда ее траекторией является окружность
нормальное ускорение
совпадает с осестремительным
![]()
по величине и направлению, а именно
по величине и направлению, а именно
 ; (2.19)
; (2.19)
касательное (тангенциальное) ускорение совпадает с вращательным
![]()
по величине и направлению, а именно
по величине и направлению, а именно
 . (2.20)
. (2.20)
Полное ускорение точки тела, вращающегося
вокруг неподвижной оси,
![]() Численное значение (модуль) его
определяется по формуле
Численное значение (модуль) его
определяется по формуле
![]() (2.21)
(2.21)
Пример 2.3.1. Груз 3 подвешен
на нерастяжимом тросе, намотанном на
барабан лебедки (рис.2.6) . Барабан радиусом
r1=
0,2 м жестко скреплен с шестерней 1
радиусом R1=
0,3 м и имеет общую с ней неподвижную
ось вращения![]() .
Шестерня 1 находится в зацеплении
с шестерней 2 радиусом r2=
0,15 м, которая приводится во вращение
(вокруг неподвижной оси
.
Шестерня 1 находится в зацеплении
с шестерней 2 радиусом r2=
0,15 м, которая приводится во вращение
(вокруг неподвижной оси
![]() ),
жестко связанной с ней рукояткой
),
жестко связанной с ней рукояткой
![]() длиной
=
0,25 м
длиной
=
0,25 м

Рис.2.6
Определить: Угловые скорости
и угловые ускорения шестеренок 1 и
2, т.е.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
а также скорость и ускорение
конца М рукоятки О2М
в момент, когда груз 3 опустится
на высоту h = 0,9 м,
если он движется по закону x
= 1+0,4t2 (x
в метрах, t
в секундах).
,
а также скорость и ускорение
конца М рукоятки О2М
в момент, когда груз 3 опустится
на высоту h = 0,9 м,
если он движется по закону x
= 1+0,4t2 (x
в метрах, t
в секундах).
Решение. В рассматриваемом механизме шестерни 1 и 2 совершают вращательное движение, а груз 3 совершает поступательное движение.
В начале движения при t = 0 координата груза была равна xo = 1 м. Когда он опустился на высоту h = 0,9 м, она стала xА = x1= 1+ 0,9 = 1,9 м. Зная, что xА= x1, найдем время, соответствующее этому перемещению груза:
xА = 1+0,4t2
= 1,9 м, или
![]()
По закону движения груза найдем его
скорость:![]() ,
,
причем вектор
![]() направлен
вниз.
направлен
вниз.
Так как трос нерастяжим, все его точки
имеют скорости, равные скорости груза
3. Следовательно, и точки обода барабана
имеют ту же скорость:
![]() .
При опускании груза барабан и шестерня
1 вращаются вокруг оси
с
угловой скоростью
.
При опускании груза барабан и шестерня
1 вращаются вокруг оси
с
угловой скоростью
![]() .
.
Скорость точек обода барабана равна![]() ,
откуда
,
откуда
![]() ,
О1 z1;
,
О1 z1;
![]() >0,т.е.
.
>0,т.е.
.
Если два тела в процессе движения
имеют общую контакта, в которой отсутствует
проскальзывание, то эти точки контакта
имеют одинаковые скорости: т.к точка
К( шестерни1и
шестерни 2. При вращении шестерни 1
с угловой скоростью
шестерня 2 будет вращаться в
противоположную сторону вокруг оси
с угловой скоростью
![]() .
При этом скорость точки К можно
представить в виде
.
При этом скорость точки К можно
представить в виде
![]() ,
,
откуда

![]() .
.
Угловая скорость рукоятки равна угловой скорости шестерни 2, т.е. ,
Поэтому скорость конца рукоятки составляет

В момент времени
![]() она равна
она равна
 Чтобы найти ускорение точки М,
надо найти предварительно угловое
Чтобы найти ускорение точки М,
надо найти предварительно угловое
ускорение шестерни 2 и рукоятки :
![]() =
=![]() т.е.
>0
и
т.е.
>0
и
![]() ,
,
а затем воспользоваться формулой (2.21)
 =
2
=
2![]() м /с2.
м /с2.
В момент времени
это ускорение равно
![]()
Ответ:
![]() =
6 рад/с;
=
12 рад/с ;
=
6 рад/с;
=
12 рад/с ;
![]() =
4 рад/с2;
=8
рад/с2;
=
4 рад/с2;
=8
рад/с2;
vМ
![]() ;
aМ
36
м /с2.
;
aМ
36
м /с2.
