Аддитивная модель

Вначале находят для каждой точки временного ряда сезонные отклонения от предполагаемой тенденции, для этого:

- находятся скользящие средние с периодом усреднения равным L;

- в случае если период сезонных колебаний представляет собой четное число, то полученные скользящие средние являются межинтервальными и для получения центрированных скользящих средних осуществляется усреднение полученных средних еще раз, но на этот раз с периодом усреднения равным двум;

- для каждого интервала времени находят сезонное отклонение СК_t как разность между фактическими значениями и соответствующими средними, т.е.:

.

Полученные сезонные отклонения являются базой для вычисления нормированных сезонных составляющих S_l для каждого интервала из периода сезонных колебаний L. Для этого полученные отклонения группируются по одинаковым номерам точек в периоде сезонных колебаний и в каждой из полученных L групп находятся средние значения сезонных отклонений . Для того чтобы сезонные составляющие не приводили к искажению тенденции при их исключении из исходного временного ряда необходимо, чтобы выполнялось условие:

.

Как правило, это условие никогда не выполняется, по этому вводится поправочный коэффициент k, равный:

;

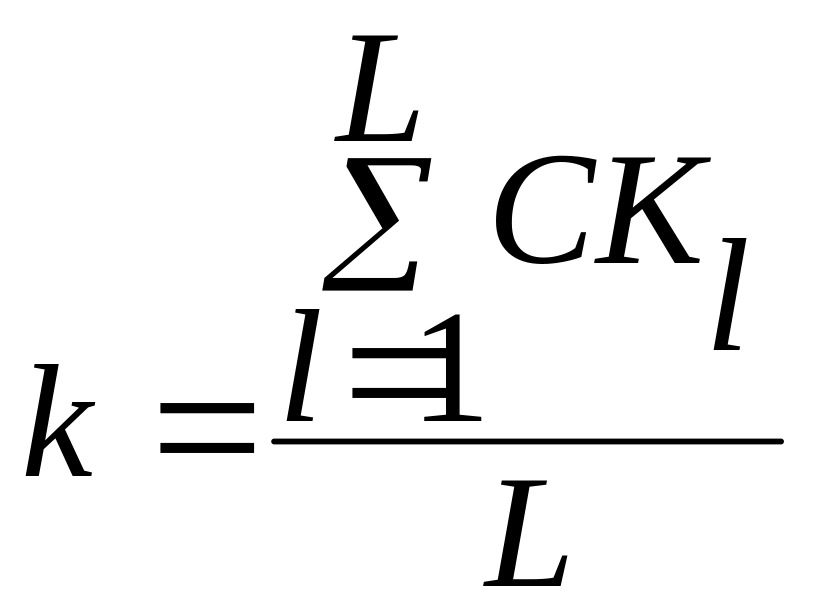Сезонная составляющая для каждой точки периода сезонных колебаний с учетом поправочного коэффициента будет равна:

В таблицах 2 - 3 приведен пример иллюстрирующий определение сезонной составляющей по аддитивной модели.

Таблица 2. Расчет сезонных отклонений от тенденции.

N	Y(t)	Скользящая средняя, L=4	Центрирован-ная скользящая средняя	Сезонные отклонения	L
1	6.0				1
2	4.4				2
3	5.0	6.10	6.250	-1.250	3
4	9.0	6.40	6.450	2.550	4
5	7.2	6.50	6.625	0.575	1
6	4.8	6.75	6.875	-2.075	2
7	6.0	7.00	7.100	-1.100	3
8	10.0	7.20	7.300	2.700	4
9	8.0	7.40	7.450	0.550	1
10	5.6	7.50	7.625	-2.025	2
11	6.4	7.75	7.875	-1.475	3
12	11.0	8.00	8.125	2.875	4
13	9.0	8.25	8.325	0.675	1
14	6.6	8.40	8.375	-1.775	2
15	7.0	8.35			3
16	10.8				4

Таблица 3. Расчет сезонной составляющей.

Показатель	Номер квартала l
	1	2	3		4
1 год	-	-	-1.250		2.550
2 год	0.575	-2.075	-1.100		2.700
3 год	0.550	-2.025	-1.475		2.875
4 год	0.675	-1.775	-		-
Среднее сезонное отклонение	0.600	-1.958	-1.275		2.708
Сумма средних сезонных отклонений	0.075
Корректирующий коэффициент k	0.075 / 4 = 0.01875
Сезонная составляющая	0.581	-1.977	-1.275	2.708

Для вычленения сезонной составляющей из исходного ряда y_t необходимо вычесть из каждой точки этого ряда соответствующую сезонную компоненту, т.е. найти разность которая будет представлять собой сумму тенденции и свободного члена . Полученный таким образом временной ряд без сезонных колебаний используется для нахождения уравнения описывающего тенденцию.