Определение сезонной составляющей временного ряда

В зависимости от характера сезонных колебаний различают два вида моделей – аддитивная и мультипликативная.

По аддитивной модели временной ряд с сезонными колебаниями представляется в виде:

где: - значение прогнозируемой переменной для -го момента времени;

- трендовая составляющая ;

- сезонная составляющая ;

- случайная ошибка.

По мультипликативной модели временной ряд с сезонными колебаниями имеет в вид:

Для решения вопроса о том какая из рассматриваемых моделей должна быть выбрана для конкретного временного ряда, необходимо построить график изменения прогнозируемой величины во времени и проанализировать изменение амплитуды сезонных колебаний (Рис.16.). В случае если амплитуда сезонных колебаний не имеет ярко выраженной тенденции к изменению во времени, то тогда может быть выбрана аддитивная модель (a), в противном случае предпочтительна мультипликативная (б).

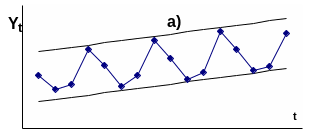
Рис 16. Временные ряды, характерные для аддитивной (а) и мультипликативной(б)моделей.

Наиболее просто сезонная составляющая может быть определена с помощью скользящих средних с периодом осреднения равным периоду сезонных колебаний L.

Скользящая средняя – это переменная значения которой равны среднему арифметическому значения исследуемой величины в точке для которой она вычисляется и значений всех точек, отстоящих от нее на 0.5*(L - 1) слева и справа в случае если L нечетное и 0.5L – если L четное. При вычислении значения скользящей средней для следующей точки временного ряда номера точек, участвующих в вычислении смещаются на единицу. Длинна периода сезонных колебаний – это число временных интервалов, через которые характер изменения временного ряда повторяется.

Таким образом для их вычисления скользящей средней вначале необходимо определить длину периода сезонных колебаний L. В простейшем случае найти ее можно на основании визуального анализа данных. Затем для каждой точки исходного временного ряда необходимо вычислить средние значения переменной . В случае если L четное, полученный ряд скользящих средних СС_t оказывается смещенным относительно на величину равную половине временного интервала. Значения скользящей средней при этом соответствуют уже не конкретным интервалам, например первому или второму интервалу, а второй половине интервала 1 и первой половине интервала 2 (рис. 17). Следующее значение скользящей средней соответствует половинам интервалов 2 и 3 и т.д. Смещенная на пол интервала скользящая средняя называется межинтервальной скользящей средняй. Для устранения возникшего смещения полученные скользящие средние с любым четным периодом осреднения необходимо еще раз усреднить с периодом усреднения, равным двум. Полученная в результате повторного осреднения скользящая средняя называется центрированной скользящей средней.

Рис. 17. Получение центрированных скользящих средних с периодом осреднения равным двум. Где:

- значения yt;

- межинтервальные скользящие средние для точек 1-2 и 2-3 соответственно;

- интервальная скользящая средняя для точки 2.

Как видно из схемы расчетов в результате усреднения число значений скользящей средней оказывается меньше числа точек исходного временного ряда на величину равную периоду осреднения L так как на краях временного ряда отсутствуют точки необходимые для нахождения скользящей средней. Потеря L точек приводит к тому, что минимальная длительность временного ряда должна быть равной хотя бы трем периодам колебаний.

Схема расчета скользящих средних для периода осреднения равного четырем (ежеквартальные данные за несколько лет) представлена в таблице 1.

Таблица 1.

номер перио-да t	фактические значения ряда	межинтервальные скользящие средние ССt	интервальные (центрированные) скользящие средние ЦССt
1
2
3
4
5
6
7

Дальнейшая схема определения сезонных колебаний различна для аддитивной и мультипликативной моделей, по этому рассмотрим их по отдельности.