
- •Содержание
- •Тема 1. Планирование, программирование и прогнозирование как формы государственного регулирования 6
- •Тема 2. Методологические основы планирования и прогнозирования 36
- •Тема 1. Планирование, программирование и прогнозирование как формы государственного регулирования Лекция 1
- •Понятие, сущность и виды общегосударственного планирования
- •Программирование как форма государственного регулирования экономики
- •Прогнозирование в системе государственного регулирования экономики
- •Система программных и прогнозных документов, используемых в государственном регулировании экономики Республики Беларусь
- •Контрольные вопросы
- •Тема 2. Методологические основы планирования и прогнозирования Лекция 2
- •Понятие и основные элементы методологии планирования и прогнозирования
- •Основные методологические принципы планирования
- •Основополагающие подходы и принципы прогнозирования
- •Система показателей, используемых в планировании и прогнозировании
- •Информационное обеспечение процессов прогнозирования и планирования
- •Экономический анализ, его содержание и место в системе планирования и прогнозирования
- •Контрольные вопросы
- •Тема 3. Экспертные (интуитивные) методы прогнозирования Лекция 3
- •Области применения и общая схема работ по разработке экспертного прогноза
- •Поиск и отбор экспертов
- •Опрос экспертов
- •Обработка количественных ответов экспертов
- •Методы экспертного прогнозирования
- •Контрольные вопросы
- •Тема 4. Прогнозирование случайной величины по выборке значений. Лекция 4
- •Случайная переменная и общая схема прогнозирования по выборке
- •Предварительный анализ данных.
- •Прогнозирование ожидаемого значения случайной величины.
- •Оценка точности прогнозирования случайной величины.
- •Контрольные вопросы
- •Тема 5. Прогнозирование с использованием регрессионной зависимости Лекция 5
- •Общая схема прогнозирования с использованием регрессионной зависимости
- •Оценка параметров уравнения регрессии
- •Проверка значимости уравнения регрессии
- •Контрольные вопросы
- •Тема 6. Прогнозирование временных рядов Лекция 6
- •Определение сезонной составляющей временного ряда
- •Аддитивная модель
- •Мультипликативная модель
- •Определение тенденции временного ряда
- •Прогнозирование случайной составляющей
- •Контрольные вопросы
- •Тема 7. Методы планирования Лекция 7
- •Балансовый метод в планировании
- •Нормативный метод планирования
- •Программно-целевой метод
- •Планирование с использованием оптимизационных моделей
- •Контрольные вопросы
- •Тема 8. Практика планирования и прогнозирования Важнейших сфер экономики Лекция 8
- •Планирование и прогнозирование экономического развития и экономического роста
- •Планирование и прогнозирование инвестиционной деятельности
- •Планирование и прогнозирование малого предпринимательства
- •Планирование и прогнозирование отраслей промышленности
- •Планирование и прогнозирование апк
- •Контрольные вопросы
- •Экзаменационные вопросы
- •Литература
- •220007, Г. Минск, ул. Московская, 17.
Оценка параметров уравнения регрессии
Для прогнозирования
с помощью уравнения регрессии необходимо
вычислить коэффициенты
![]() и
и
![]() уравнения регрессии. И здесь существует
еще одна проблема сказывающаяся на
точности прогнозирования. Она заключается
в том, что обычно нет всех возможных
значений переменных Х и У, т.е. генеральная
совокупность совместного распределения
в задачах прогнозирования не известна,
известна только выборка из этой
генеральной совокупности. В результате
этого при прогнозировании помимо
случайной составляющей возникает еще
один источник ошибок – ошибки, вызванные
не полным соответствием выборки
генеральной совокупности и порождаемыми
этим погрешностями в определении
коэффициентов уравнения регрессии.
уравнения регрессии. И здесь существует
еще одна проблема сказывающаяся на
точности прогнозирования. Она заключается
в том, что обычно нет всех возможных
значений переменных Х и У, т.е. генеральная
совокупность совместного распределения
в задачах прогнозирования не известна,
известна только выборка из этой
генеральной совокупности. В результате
этого при прогнозировании помимо
случайной составляющей возникает еще
один источник ошибок – ошибки, вызванные
не полным соответствием выборки
генеральной совокупности и порождаемыми
этим погрешностями в определении
коэффициентов уравнения регрессии.
Иными словами
вследствие того, что генеральная
совокупность не известна, точные значения
коэффициентов
и
уравнения регрессии определить не
возможно. Используя выборку из этой
неизвестной генеральной совокупности
можно лишь получить оценки
![]() и
истинных коэффициентов
и
.
и
истинных коэффициентов
и
.
Для того чтобы
ошибки прогнозирования в результате
такой замены были минимальными, оценку
необходимо осуществлять методом который
гарантирует несмещенность и эффективность
полученных значений. Метод обеспечивает
несмещенные оценки, если при
неоднократном его повторении с новыми
выборками из одной и той же генеральной
совокупности обеспечивается выполнение
условия
![]() и
и
![]() .
Метод обеспечивает эффективные оценки,
если при неоднократном его повторении
с новыми выборками из одной и той же
генеральной совокупности обеспечивается
минимальная дисперсия коэффициентов
a и b, т.е.
выполняются условия
.
Метод обеспечивает эффективные оценки,
если при неоднократном его повторении
с новыми выборками из одной и той же
генеральной совокупности обеспечивается
минимальная дисперсия коэффициентов
a и b, т.е.
выполняются условия
![]() и
и
![]() .
.
В теории вероятности доказана теорема согласно которой эффективность и несмещенность оценок коэффициентов уравнения линейной регрессии по данным выборки обеспечивается при применении метода наименьших квадратов.
Суть метода
наименьших квадратов заключается в
следующем. Для каждой из
точек выборки записываются уравнение
вида
![]() .
Затем находятся ошибка
.
Затем находятся ошибка
![]() между расчетным и фактическим значениями
между расчетным и фактическим значениями
![]() .
Решение оптимизационной задачи по
нахождению таких значений
и
которые обеспечивают минимальную сумму
квадратов ошибок для всех n
точек, т.е. решение задачи поиска
.
Решение оптимизационной задачи по
нахождению таких значений
и
которые обеспечивают минимальную сумму
квадратов ошибок для всех n
точек, т.е. решение задачи поиска
![]() ,
дает несмещенные и эффективные оценки
коэффициентов
и
.
Для случая парной линейной регрессии
это решение имеет вид:
,
дает несмещенные и эффективные оценки
коэффициентов
и
.
Для случая парной линейной регрессии
это решение имеет вид:
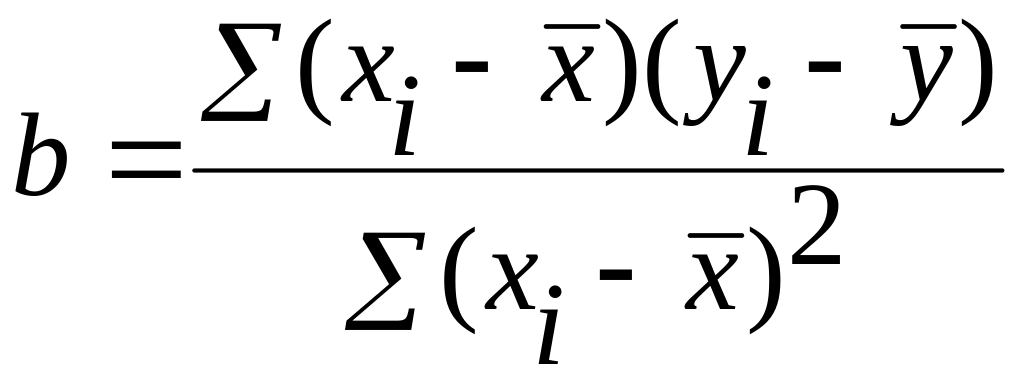
![]()
Следует отметить, что полученные таким образом по выборке несмещенные и эффективные оценки истинных значений коэффициентов регрессии для генеральной совокупности вовсе не гарантируют от ошибки при однократном применении. Гарантия заключается в том, что, в итоге многократного повторения этой операции с другими выборками из той же генеральной совокупности, гарантирована меньшая сумма ошибок по сравнению любым другим способом и разброс этих ошибок будет минимален.
Полученные
коэффициенты уравнения регрессии
определяют положение регрессионной
прямой, она является главной осью облака
образованного точками исходной выборки.
Оба коэффициента имеют вполне определенный
смысл. Коэффициент
показывает значение
![]() при
при
![]() ,
но в многих случаях
не имеет смысла, кроме того часто
,
но в многих случаях
не имеет смысла, кроме того часто
![]() также не имеет смысла, по этому приведенной
трактовкой коэффициента
нужно пользоваться осторожно. Более
универсальная трактовка смысла
также не имеет смысла, по этому приведенной
трактовкой коэффициента
нужно пользоваться осторожно. Более
универсальная трактовка смысла
![]() заключается в следующем. Если
,
то относительное изменение независимой
переменной (изменение в процентах)
всегда меньше чем относительное изменение
зависимой переменной.
заключается в следующем. Если
,
то относительное изменение независимой
переменной (изменение в процентах)
всегда меньше чем относительное изменение
зависимой переменной.
Коэффициент
показывает насколько единиц изменится
зависимая переменная при изменении
независимой переменной на одну единицу.
Коэффициент
часто называют коэффициентом регрессии
подчеркивая этим, что он важнее чем
.
В частности, если вместо значений
зависимой и независимой переменных
взять их отклонения от своих средних
значений, то уравнение регрессии
преобразуется к виду
![]() .
Иными словами в системе преобразованных
координат любая линия регрессии проходит
через начало координат (рис 13) и коэффициент
отсутствует.
.
Иными словами в системе преобразованных
координат любая линия регрессии проходит
через начало координат (рис 13) и коэффициент
отсутствует.

Рис 13. Положение регрессионной зависимости в системе преобразованных координат.
Параметры уравнения регрессии говорят нам о том, как связаны между собой зависимая и независимая переменная, но ничего не говорят о степени тесноты связи, т.е. показывают положение главной оси облака данных, но не ничего не говорит о степени тесноты связи (насколько узко или широко облако).
О степени тесноты
связи можно судить по линейному
коэффициенту корреляции
![]() :
:
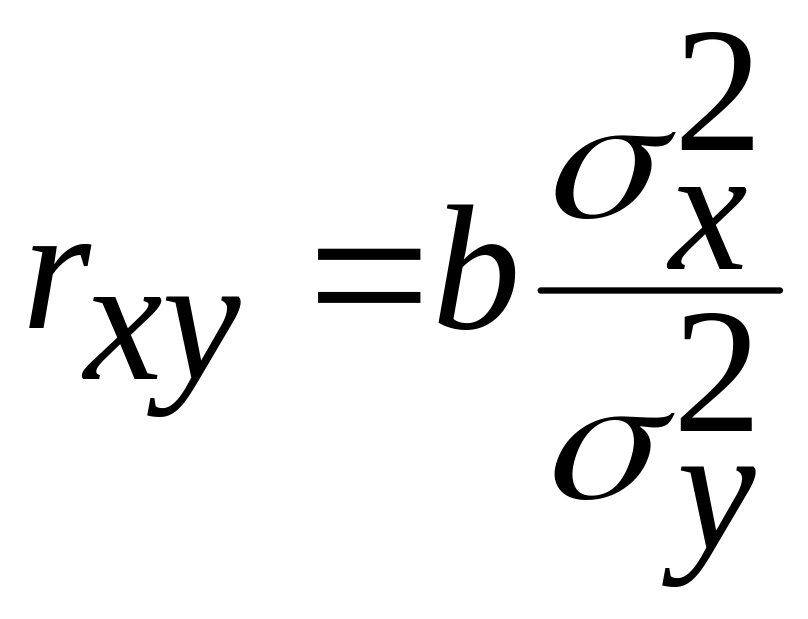
Коэффициент
корреляции меняется в пределах от –1
до +1. Чем он ближе по абсолютному значению
к единице, тем сильнее зависимость (тем
сильнее облако данных прижато к своей
главной оси). Если
![]() то наклон линии регрессии отрицателен,
чем ближе он к 0 тем слабее связь, при
то наклон линии регрессии отрицателен,
чем ближе он к 0 тем слабее связь, при
![]() линейной связи между переменными нет,
а при
линейной связи между переменными нет,
а при
![]() связь переменных является функциональной.
Влияние коэффициента корреляции на
форму и положения облака данных
проиллюстрировано на рис 14.
связь переменных является функциональной.
Влияние коэффициента корреляции на
форму и положения облака данных
проиллюстрировано на рис 14.

Рис 14. Влияние формы и положения облака данных на парный линейный коэффициент корреляции.
Коэффициент
корреляции позволяет получить оценку
точности уравнения регрессии - коэффициент
детерминации
![]() .
Для парной линейной регрессии он равен
квадрату коэффициента корреляции, для
многомерной или нелинейной регрессии
его определение сложнее. Коэффициент
детерминации
показывает, сколько процентов дисперсии
зависимой переменной объясняется
уравнением регрессии, а
.
Для парной линейной регрессии он равен
квадрату коэффициента корреляции, для
многомерной или нелинейной регрессии
его определение сложнее. Коэффициент
детерминации
показывает, сколько процентов дисперсии
зависимой переменной объясняется
уравнением регрессии, а
![]() - сколько процентов дисперсии осталась
необъясненной (зависит от неконтролируемого
нами случайного члена
).
- сколько процентов дисперсии осталась
необъясненной (зависит от неконтролируемого
нами случайного члена
).
