
- •Математические методы исследований в экономике
- •Себестоимость изделия. Оценка прибыльности и окупаемости.
- •Адаптивное назначение цены продукции на конкурентном рынке
- •Поведение производственного объекта в рыночных условиях.
- •Численные вычисления:
- •Решение по второму варианту. Изменение доли затрат на приобретение основных производственных фондов.
- •Многопродуктовый простой производственный объект.
- •Решение задачи.
Многопродуктовый простой производственный объект.
Цель работы: изучение математических моделей многопродуктового производственного объекта; закрепление теоретического материала расчетом примеров определения возможностей объекта по выпуску продукции различного вида.
Вариант №1
Компонент |
Изделие |
|||
|
А1 |
А2 |
А3 |
А4 |
a1 |
2,5 |
1 |
0 |
3 |
а2 |
0 |
2 |
1 |
3 |
а3 |
1,5 |
4 |
0 |
0 |
а4 |
0,7 |
2 |
2 |
3 |
а5 |
1 |
0 |
3 |
4 |
Данные |
N1 |
N2 |
N3 |
N4 |
V10 |
V20 |
V30 |
V40 |
V50 |
L0 |
mL1 |
mL2 |
mL3 |
mL4 |
Значения |
0.12 |
0.28 |
0.2 |
0.4 |
15 |
10 |
23 |
20 |
22 |
7 |
0.3 |
1.5 |
1.5 |
1.1 |
Дано:
Количество видов изделий n и нормы затрат компонентов на изготовление единицы изделия. Доли выпуска каждого вида изделия в общем объеме выпуска Nj. Ограничения на наличии компонентов Vi0. Ограничение на наличие персонала L0. Нормативы трудозатрат на изготовление изделия каждого вида mLj.
Определить: количество изделий каждого вида xj, которое предприятие сможет выпустить, исходя из наличия компонентов. Ннеобходимую численность персонала для выпуска каждого вида изделий.
Порядок решения задачи:
Записать систему неравенств (**)
Определить из (**) с учетом (***) и (****) ограничения на Х
Вычислить из (3*)
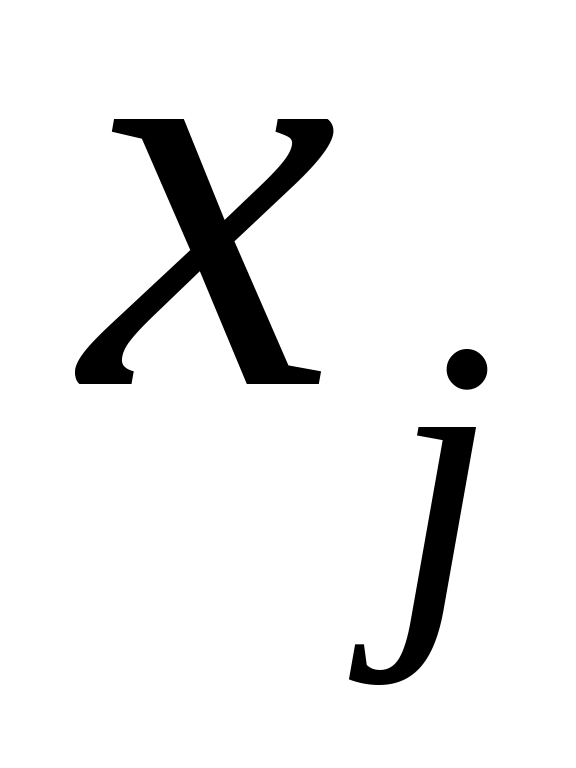
Вычислить из (1*)
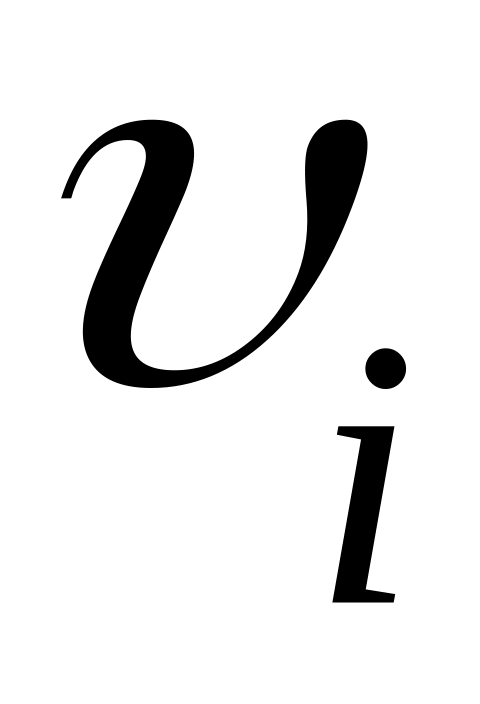
Вычислить из (1*)
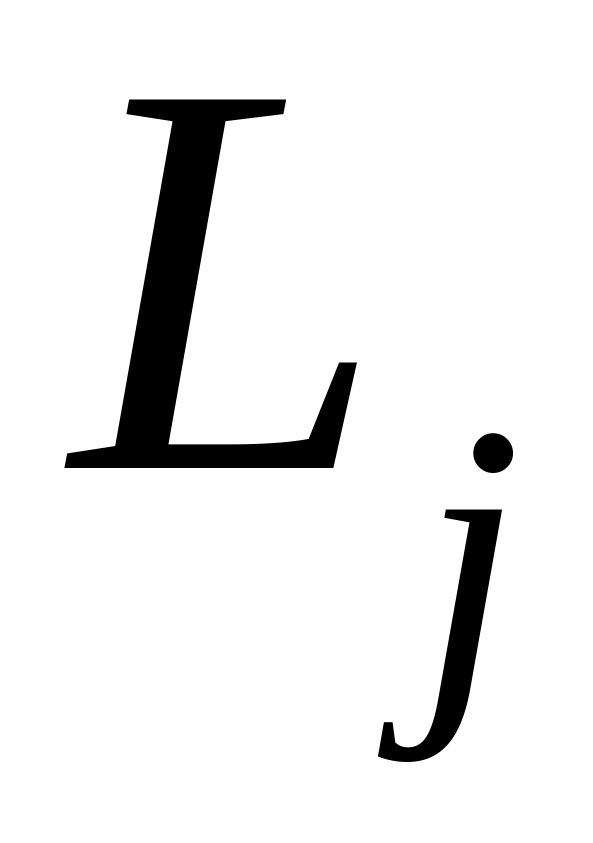
Произвести сравнение потребного и наличного
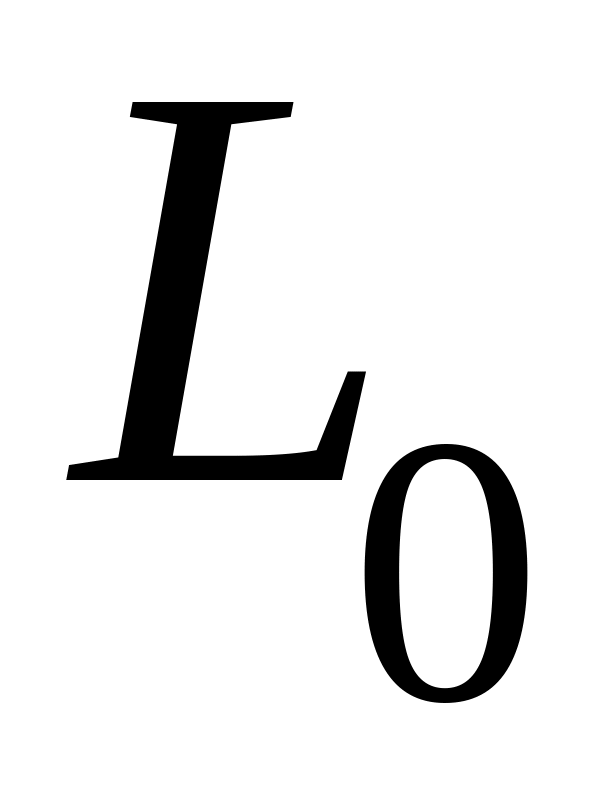 количества персонала.
количества персонала.
Решение задачи.
На производственном
участке производится сборка четырех
видов изделий:
![]() Максимально возможное количество
персонала – 7 рабочих одинаковой
специальности, т. е L0=7.
Для производства изделий используются
5 видов компонентов.
Максимально возможное количество
персонала – 7 рабочих одинаковой
специальности, т. е L0=7.
Для производства изделий используются
5 видов компонентов.
Следующая система уравнений описывает, сколько компонентов требуется для производства каждого изделия.
|
|
|
|
|
|
---------- |
|
----------- |
|
|
|
|
|
----------- |
------------ |
|
|
|
|
|
--------- |
|
|
![]() -
количество деталей вида
-
количество деталей вида
![]() ,
необходимых для выпуска продукции
,
необходимых для выпуска продукции
![]() .
.
Зададим ограничения на общее количество деталей по их видам.
![]()
![]()
![]() (1*)
(1*)
![]()
![]()
![]() -
общее количество деталей
-
общее количество деталей
![]() -го
вида.
-го
вида.
Зададим ограничения на численность рабочего персонала.
![]()
где
![]() -
численность персонала, работающего над
изготовлением j
– го вида изделия.
-
численность персонала, работающего над
изготовлением j
– го вида изделия.
![]() (2*)
(2*)
![]() -
количество деталей j-го
вида небходимое для производства.
-
количество деталей j-го
вида небходимое для производства.
![]() -
норматив трудовых затрат на изделие
j-го
вида.
-
норматив трудовых затрат на изделие
j-го
вида.
Уравнения из таблицы и система (*), определяют взаимосвязь элементов производства на участке.
![]()
![]()
![]() (3*)
(3*)
![]()
![]()
![]() - общее количество
деталей различных видов, которые имеются
на складе и могут быть доставлены на
склад за единицу времени.
- общее количество
деталей различных видов, которые имеются
на складе и могут быть доставлены на
склад за единицу времени.
Определим
![]() из уравнения
из уравнения
![]() (4*)
(4*)
где Х - суммарный выпуск предприятия с учетом всех видов изделий. Определяется следующим образом.
![]()
=>
![]() (5*)
(5*)
Определим, какое количество деталей различных видов необходимо для производства продукции.
![]()
![]()
![]()
![]()
Проверим:
![]()
Определим общее
количество деталей
![]()
![]() -го
вида необходимых для выпуска продукции.
-го
вида необходимых для выпуска продукции.
![]()
![]()
![]()
![]()
![]()
Вычислим численность персонала, работающего над изготовлением j – го вида изделия.
![]()
![]()
![]()
![]()
Пусть численные значения долей и ограничения на количество деталей равны следующим величинам
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() (*6)
(*6)
Определим программу выпуска каждого вида изделия, расход деталей на каждый вид, потребное количество персонала. Подставляя выражение (5*) в систему уравнений (3*) получим:
![]()
![]()
![]()
![]()
![]()
Подставляя численные значения величин из (6*) в полученную систему неравенства, получим.
![]()
![]()
![]() (7*)
(7*)
![]()
![]()
Из системы уравнений (7*) получим неравенства.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Таким образом,
имеем решение
системы неравенств (7*), т.е возможность
выпуска предприятием указанных изделий
в сумме ограничена числом 5 и это
ограничение определено наличием на
складе деталей второго вида (![]() ).
Пусть
).
Пусть
![]() .
Тогда из уравнения (4*) получим программу
выпуска.
.
Тогда из уравнения (4*) получим программу
выпуска.
![]()
![]()
![]()
![]()
Дробность программы
выпуска означает, что за рассматриваемую
единицу времени изготавливается не
целое число изделий. Некоторые из них
изготовлены частично. Расход каждого
вида компонентов получим из (3*), подставляя
туда найденные значения
![]() :
:
![]()
![]()
![]()
![]()
![]()
Пусть нормативы
трудозатрат равны
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Тогда потребная численность персонала по каждому виду изделия определится из соотношения
![]()
![]()
![]()
![]()
Таким образом, необходимое количество персонала на участке составляет 10 человек, а всего работают 7 человек, что недостаточно для стабильного выпуска продукции.
Выводы.
Возможность выпуска предприятием указанных изделий в сумме ограничена числом 5 и это ограничение определено наличием на складе деталей второго вида ( ). Наличное количество персонала недостаточно для стабильной работы предприятия, т.к его значение существенно отличается от необходимого количества.
