
- •1. Расчет режима трехфазного короткого замыкания в сложной электрической сети
- •Исходные параметры оборудования
- •Принимаем базисные единицы:
- •1.1. Расчет параметров схемы замещения
- •6. Система
- •7. Воздушные линии
- •1.2. Преобразование схемы замещения
- •1.3. Расчет коэффициентов токораспределения
- •1.3.1. Расчет коэффициентов токораспределения ветвей
- •1.3.2. Расчет коэффициентов токораспределения ветвей фрагмента схемы, представленного на рис. 1.3
- •1.3.3. Расчет коэффициентов токораспределения ветвей источников питания
- •1.4.1. Параметры тока кз в месте кз
- •1.4.2. Параметры тока кз, протекающего через генераторный выключатель
- •1.4.3. Периодические слагаемые токов источников питания, приведенные к ступеням напряжения этих источников
- •1.4.5. Расчет токов короткого замыкания для времени t
- •2. Расчет режима несимметричного короткого замыкания в сложной электрической сети
- •2.1. Схема замещения прямой последовательности
- •2.2. Расчет коэффициентов токораспределения схемы прямой последовательности
- •2.3. Схема замещения обратной последовательности
- •2.4. Схема замещения нулевой последовательности
- •2.5. Преобразование схемы нулевой последовательности и расчет
- •2.6. Расчет параметров аварийного режима для начального момента времени
- •2.6.1. Параметры режима несимметричного кз в точке кз
- •Значения дополнительного сопротивления и коэффициента
- •2.6.2. Расчет фазных токов, протекающих в л1
- •2.6.3. Расчет остаточных напряжений
- •Литература
- •Оглавление
- •Владимир Иванович Готман электромагнитные переходные процессы в электроэнергетических системах
2.6. Расчет параметров аварийного режима для начального момента времени
2.6.1. Параметры режима несимметричного кз в точке кз
Согласно
методу симметричных составляющих расчет
несимметричных КЗ осуществляется по
правилу эквивалентности тока прямой
последовательности, в соответствии с
которым ток прямой последовательности
любого несимметричного КЗ в реальной
точке K численно равен
току трехфазного КЗ в некоторой фиктивной
точке, удаленной от реальной точки на
дополнительный реактанс
![]() :
:
 ,
,
где
![]() для различных видов КЗ определяется по
табл. 2.2.
для различных видов КЗ определяется по
табл. 2.2.
Таблица 2.2
Значения дополнительного сопротивления и коэффициента
Вид замыкания |
|
|
|
Трехфазное |
3 |
0 |
1 |
Двухфазное |
2 |
|
|
Однофазное |
1 |
|
3 |
Двухфазное на землю |
1.1 |
// |
|
Модуль периодической слагаемой тока поврежденной фазы (фаз) в точке любого несимметричного КЗ (n) определяется по выражению
![]() ,
,
где
![]() – коэффициент пропорциональности,
зависит от вида КЗ согласно табл. 2.2.
– коэффициент пропорциональности,
зависит от вида КЗ согласно табл. 2.2.
Отметим,
что токи обратной (![]() )
и нулевой (
)
и нулевой (![]() )
последовательностей по месту КЗ
пропорциональны току прямой
последовательности. Симметричные
составляющие напряжения по месту КЗ
определяются выражениями (см. табл.
2.3):
)
последовательностей по месту КЗ
пропорциональны току прямой
последовательности. Симметричные
составляющие напряжения по месту КЗ
определяются выражениями (см. табл.
2.3):
![]() ;
;
![]() ;
;
![]() .
.
Проведем расчет
интересующих параметров по месту![]() .
.
Имеем:
![]() ;
;
![]() ;
;
![]() .
.
Примем фазу ЭДС
![]()
Действующее значение периодической слагаемой тока прямой последовательности особой фазы А
 ,
,
где
![]() //
//
![]() //
//
![]() .
.
Симметричные составляющие токов обратной и нулевой последовательностей:
 ;
;
 .
.
Модуль
периодической слагаемой тока короткого
замыкания поврежденных фаз
![]()
![]() кА,
кА,
где
 .
.
Ударный ток КЗ
![]() кА,
кА,
где
![]() ;
;
![]() с по данным табл. 1.5, позиция 11.
с по данным табл. 1.5, позиция 11.
2.6.2. Расчет фазных токов, протекающих в л1
Для двухцепной воздушной линии (Л1) имеем коэффициенты токораспределения прямой, обратной и нулевой последовательностей для эквивалентной ветви (элемент схемы замещения 13):
![]() ;
;
;
;
![]() .
.
Симметричные составляющие токов фазы "А" Л1 в расчете на одну цепь:
 ;
;
 ;
;
 .
.
Т аблица
2.3
аблица
2.3
Симметричные составляющие I и U в месте несимметричных КЗ для особой фазы "А"
Рассчитываемые величины и их обозначения |
Расчетные выражения |
|||
|
|
двухфазное на землю |
||
Ток прямой последовательности |
|
|
|
|
Ток обратной последовательности |
|
|
|
|
Ток нулевой последовательности |
|
0 |
|
|
Напряжение прямой последовательности |
|
|
|
|
Напряжение обратной последовательности |
|
|
- |
|
Напряжение нулевой последовательности |
|
0 |
- |
|


Фазные токи Л1 (кА):
![]()
=
![]() кА;
кА;
![]()

![]() кА.
кА.
По этим результатам на рис. 2.6, а приведена векторная диаграмма токов. Для построения векторной диаграммы токов по месту КЗ (рис. 2.5, а) имеем симметричные составляющие токов (кА):
![]() кА;
кА;
![]() кА;
кА; ![]() кА.
кА.
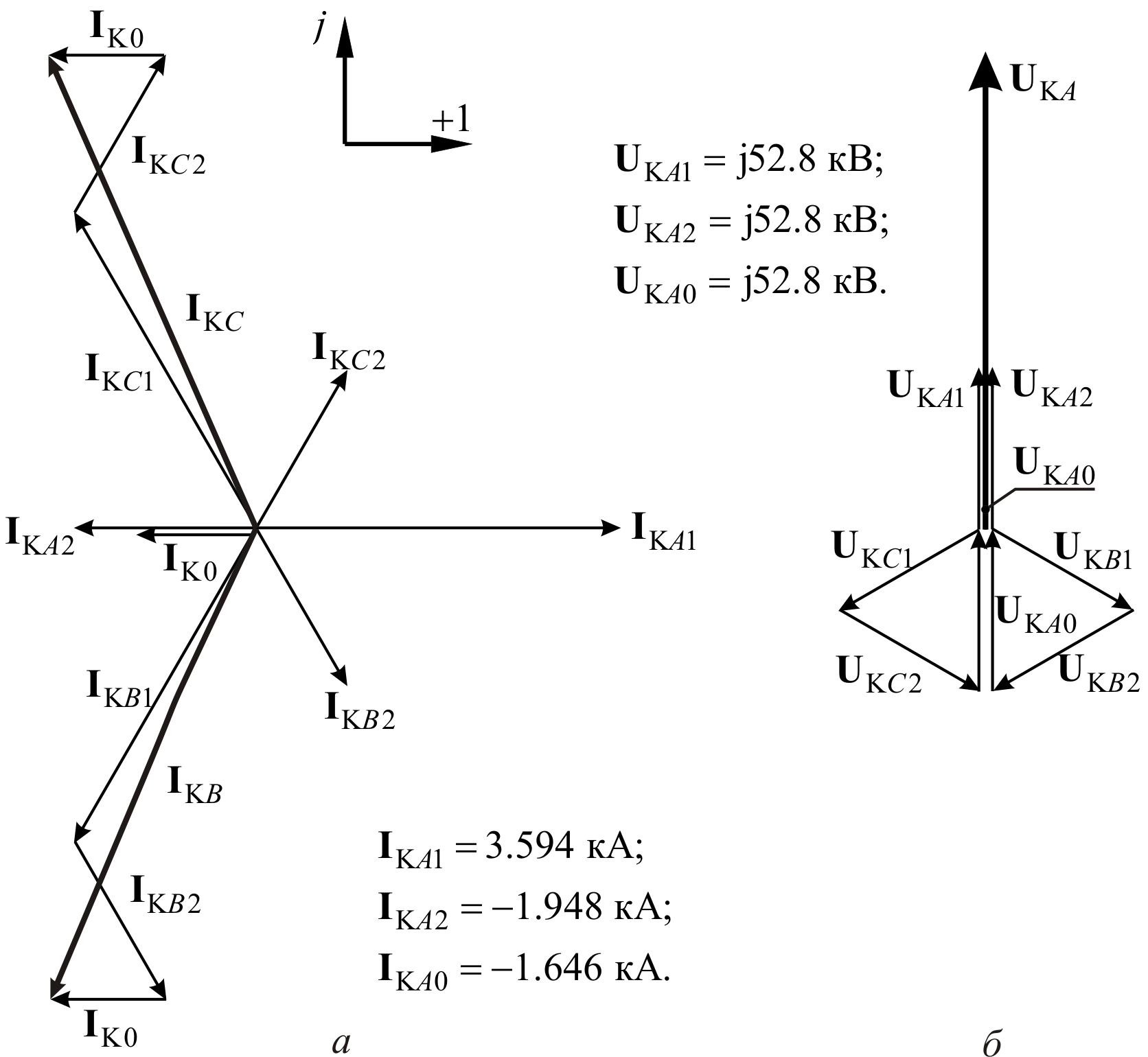
Рис. 2.5. Векторная диаграмма токов (а) и напряжений (б) в точке



