
- •1. Расчет режима трехфазного короткого замыкания в сложной электрической сети
- •Исходные параметры оборудования
- •Принимаем базисные единицы:
- •1.1. Расчет параметров схемы замещения
- •6. Система
- •7. Воздушные линии
- •1.2. Преобразование схемы замещения
- •1.3. Расчет коэффициентов токораспределения
- •1.3.1. Расчет коэффициентов токораспределения ветвей
- •1.3.2. Расчет коэффициентов токораспределения ветвей фрагмента схемы, представленного на рис. 1.3
- •1.3.3. Расчет коэффициентов токораспределения ветвей источников питания
- •1.4.1. Параметры тока кз в месте кз
- •1.4.2. Параметры тока кз, протекающего через генераторный выключатель
- •1.4.3. Периодические слагаемые токов источников питания, приведенные к ступеням напряжения этих источников
- •1.4.5. Расчет токов короткого замыкания для времени t
- •2. Расчет режима несимметричного короткого замыкания в сложной электрической сети
- •2.1. Схема замещения прямой последовательности
- •2.2. Расчет коэффициентов токораспределения схемы прямой последовательности
- •2.3. Схема замещения обратной последовательности
- •2.4. Схема замещения нулевой последовательности
- •2.5. Преобразование схемы нулевой последовательности и расчет
- •2.6. Расчет параметров аварийного режима для начального момента времени
- •2.6.1. Параметры режима несимметричного кз в точке кз
- •Значения дополнительного сопротивления и коэффициента
- •2.6.2. Расчет фазных токов, протекающих в л1
- •2.6.3. Расчет остаточных напряжений
- •Литература
- •Оглавление
- •Владимир Иванович Готман электромагнитные переходные процессы в электроэнергетических системах
2.3. Схема замещения обратной последовательности
Схема
обратной последовательности по структуре
полностью совпадает со схемой прямой
последовательности. Отличие схемы
обратной последовательности состоит
в том, что в ней ЭДС всех генерирующих
источников питания принимаются равными
нулю, а в месте короткого замыкания
приложено напряжение обратной
последовательности
![]() .
Кроме того, для генераторов сопротивление
обратной последовательности
.
Кроме того, для генераторов сопротивление
обратной последовательности
![]() ;
для всех прочих элементов сопротивление
обратной и прямой последовательностей
одинаковы. В практических расчетах
можно принимать
;
для всех прочих элементов сопротивление
обратной и прямой последовательностей
одинаковы. В практических расчетах
можно принимать![]() .
В силу этого допущения имеем
.
В силу этого допущения имеем
![]() .
.
Вследствие
того, что в схеме обратной последовательности
отсутствует ЭДС источников питания,
коэффициенты токораспределения прямой
![]() и обратной
и обратной
![]() последовательностей не равны. Для
интересующей ветви имеем
последовательностей не равны. Для
интересующей ветви имеем
![]() .
.
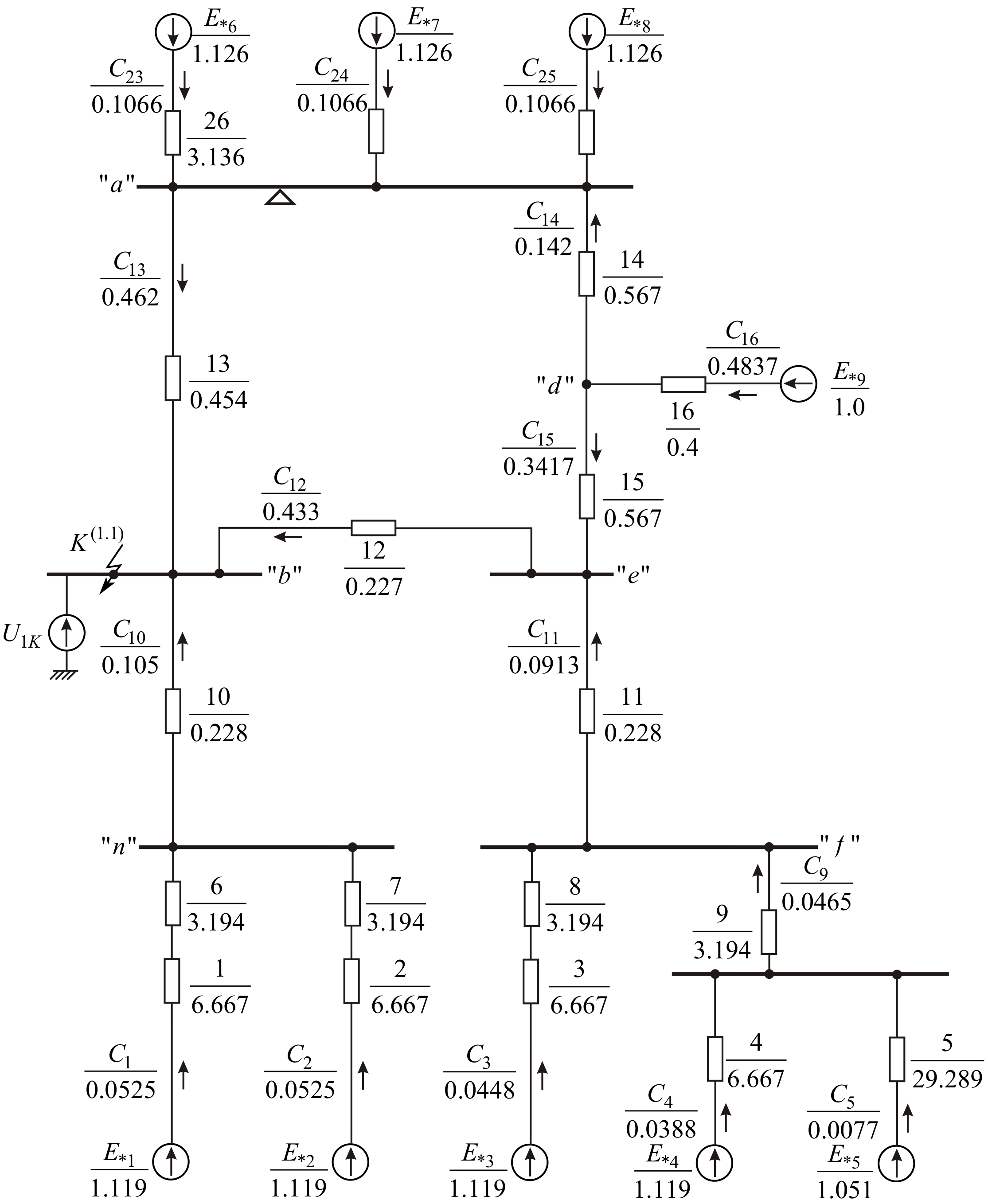
Рис. 2.2. Схема замещения прямой последовательности электрической сети
2.4. Схема замещения нулевой последовательности
Схема
нулевой последовательности существенно
отличается от схемы прямой последовательности
и в значительной мере определяется
соединением обмоток трансформаторов.
Началом схемы нулевой последовательности
считают точку, в которой объединены
ветви с нулевым потенциалом, а ее концом
– место КЗ, в котором приложено
![]() .
.
Для рассматриваемого примера схема нулевой последовательности представлена на рис. 2.3. В нее входят все ВЛ-220 кВ, автотрансформаторы АТ-1–АТ-3 обмотками высокого и низкого напряжений (обмотки среднего напряжения "звезда с нулем" находятся на холостом ходу и током не обтекаются), трансформаторы Т1, Т2 всеми тремя обмотками и "система". Для автотрансформаторов (АТ-1–АТ3), трансформаторов (Т1, Т2) и "системы" сопротивления нулевой последовательности равны сопротивлениям прямой последовательности.
Сопротивление нулевой последовательности ЛЭП существенно больше сопротивления прямой последовательности.
В
упрощенных практических расчетах
сопротивление нулевой последовательности
(
)
воздушных линий электропередач
допускается определять через коэффициент
![]() ,
значение которого зависит от конструктивного
исполнения ЛЭП. Приближенные значения
коэффициентов приведены в табл. 2.1.
,
значение которого зависит от конструктивного
исполнения ЛЭП. Приближенные значения
коэффициентов приведены в табл. 2.1.
Таблица 2.1
Исполнение воздушной линии электропередачи |
|
Одноцепная линия без троса |
3.5 |
Одноцепная линия со стальным тросом |
3.0 |
Одноцепная линия с хорошо проводящим тросом |
2.0 |
Двухцепная линия без троса |
5.5 |
Двухцепная линия со стальным тросом |
4.7 |
Двухцепная линия с хорошо проводящим тросом |
3.0 |
Примем следующие конструктивные исполнения ВЛ:
Л1 – двухцепная с хорошо проводящим тросом;
Л2, Л3 – одноцепные со стальным тросом;
Л4 – одноцепная без троса.
В соответствии с этим и данными табл. 2.1 имеем следующие значения сопротивлений нулевой последовательности ВЛ:
![]() ;
;
![]() ;
;
![]() .
.
2.5. Преобразование схемы нулевой последовательности и расчет
В силу значительной аналогии процесса упрощения схемы прямой и нулевой последовательностей мы приведем его в сокращенной форме.
По данным рис. 2.3 находим эквиваленты:
относительно узла "а"
![]() ;
;
относительно узла "b"
![]() //
//![]() ;
;
относительно узла "e"
![]() .
.
Преобразование фрагмента схемы ЛЭП-С, окаймленного узлами "а", "b", "е", "d", "система", как и ранее, проведем в два этапа, используя рис. 2.1.
На первом этапе "звезду" сопротивлений 14, 15, 16 (см. рис. 2.1, б) заменяем "треугольником" сопротивлений:
![]() ;
; ![]() ;
;
![]() .
.
И далее "треугольник" сопротивлений 12, 13, 32 (см. рис. 2.1, а) заменяем "звездой" сопротивлений:
![]() ;
;
![]() ;
;
![]() .
.
В результате проведенных преобразований схема имеет разомкнутую структуру (см. рис. 2.4).
Завершающий этап преобразований по схеме (см. рис. 2.4):
относительно узла "m":
//![]() ;
;
![]() //
//![]() ;
;
относительно узла "b":
![]() //
//![]() .
.
Суммарный реактанс схемы нулевой последовательности
![]() //
//![]() .
.
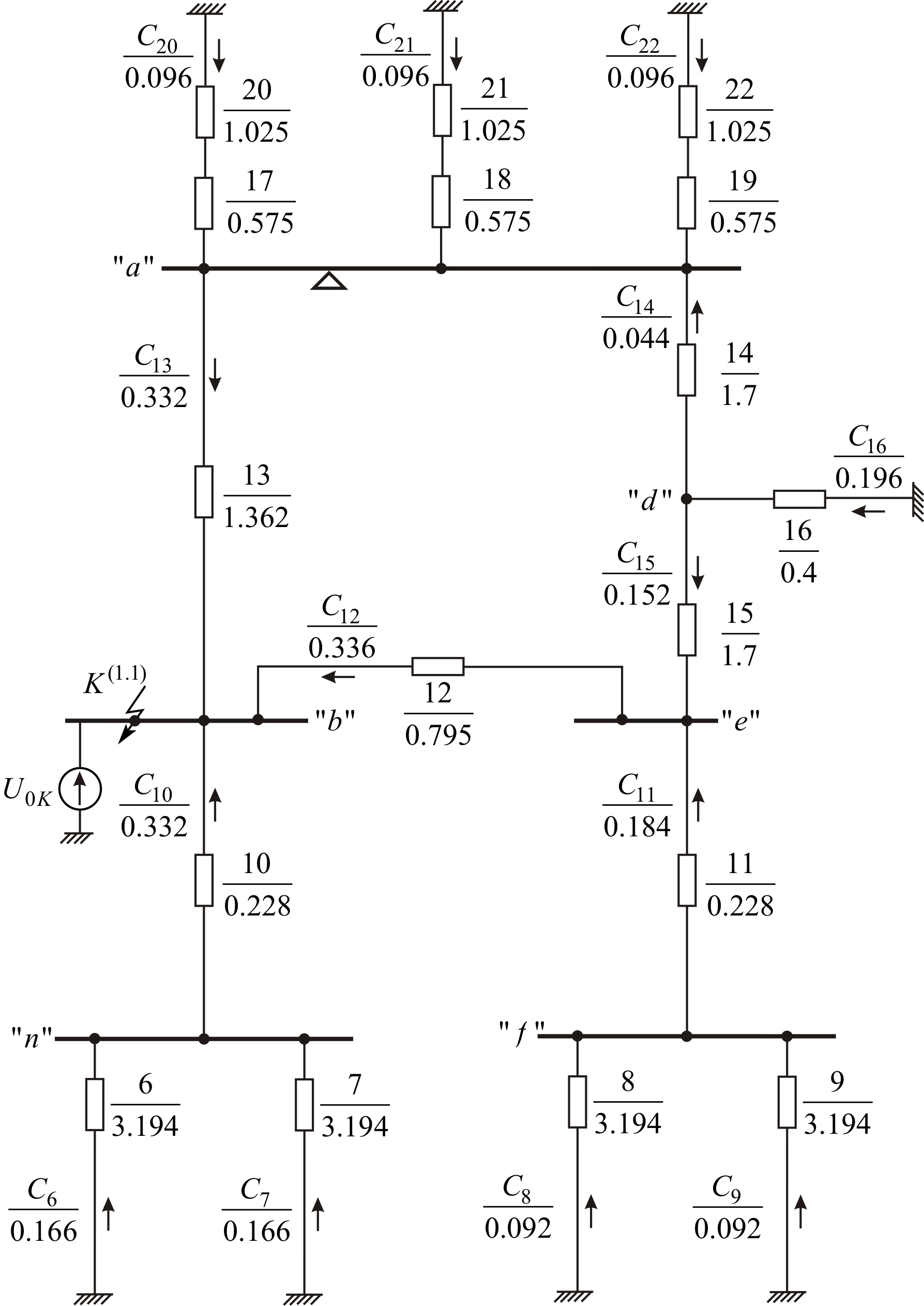
Рис. 2.3. Схема замещения нулевой последовательности электрической сети
Коэффициенты
токораспределения преобразованной и
исходной схем замещения нулевой
последовательности представлены на
рис. 2.4 и 2.3. Отметим, что практически для
решения задачи необходим только
коэффициент токораспределения ветви
13, равный
![]() .
.

Рис. 2.4. Преобразованная схема замещения нулевой последовательности
