Применение первого закона термодинамики к различным процессам

Изотермический процесс. В идеальном газе внутренняя энергия определяется абсолютной температурой. При изо­термическом расширении или сжатии газа его температура не меняется. В изотермическом процессе изменение внут­ренней энергии равно нулю: =0. На основании первого закона термодинамики при изотермическом расширении га­за переданное количество теплоты Q равно работе А, совершенной газом: Q = A.

Работа же в данном процессе

.

Изохорный процесс. При изохорном процессе работа га­за равна нулю, поэтому изменение внутренней энергии идеального газа равно полученному количеству теплоты Q.

Итак, при изохорном процессе Q = ∆U = .

Изобарный процесс. Изобарное расширение газа проис­ходит при передаче ему количества теплоты Q. В результа­те нагревания газа происходит увеличение его внутренней энергии и совершение работы расширения: .

Адиабатный процесс. Адиабатным называется процесс изменения объема, давления и температуры газа при отсут­ствии теплообмена с окружающими телами, то есть при ус­ловии Q = 0.

При адиабатном расширении газ совершает работу за счет уменьшения внутренней энергии: = – А. Поэтому температура газа при адиабатном расширении понижается. Используя полученное выражение, а также уравнение состояния идеального газа, можно получить уравнение адиабатного процесса (уравнение Пуассона):

= const,

где – коэффициент Пуассона.

Теплоемкость газов. Теплоемкостью называется коли­чество теплоты, необходимой для нагревания тела на 1 К. Для анализа теплоемкости газов удобно использовать мо­лярную теплоемкость, которая равна количеству теплоты, необходимой для нагревания одного моля вещества на 1 К:

или, используя уравнение состояния идеального газа, можно рассчитать молярную теплоемкость каждого процесса по формуле

Единица молярной теплоемкости -

Молярная теплоемкость газа зависит от процесса с ним производимого. Для изохорного процесса соответственно можем получить

в случае изобарного процесса

Следовательно, для γ можно получить:

.

Задание к лабораторной работе

Данная программа предназначена для проведения лабо­раторных работ по термодинамике для студентов техниче­ских вузов. Она позволяет моделировать и получать коли­чественные характеристики любого термодинамического (квазистатического) процесса. Также имеется возмож­ность увидеть гра­фики этих процес­сов при любой функциональной за­висимости коорди­натных осей.

Лабораторная установка представляет собой цилиндр с подвижным поршнем, заполненный двухатомным идеаль­ным газом (молярную массу можно выбирать произволь­но). Газ в установке можно нагревать (охлаждать). В про­грамме предусмотрена возможность помещения установки в термостат. Для начала эксперимента не­обходимо ввести начальные значе­ния необходимых вам параметров. Невведенные параметры вычисляются через известные или им присваиваются (в случае нехватки параметров для вычисления) значения па­раметров при нормальных условиях.

Изотермический процесс

1. Выберите в окне программы значение массы газа, степень свободы и молярную массу газа (рис.2). Занесите в табл.1 начальные параметры газа.

2. Для проведения с газом изотермического процесса необходимо рядом с буквой Т установить флажок.

3. Уменьшите объём газа перетаскиванием бегунка полосы прокрутки, расположенного справа от рисунка.

4. Занесите в табл. 1 конечные параметры газа, а также количество теплоты, сообщенное газу, изменение внутрен­ней энергии и совершенную газом работу.

5. Рассчитайте теплоемкость газа в данном процессе.

6. Зарисуйте графики изотермического процесса в коор­динатах рV, рТ, VT.

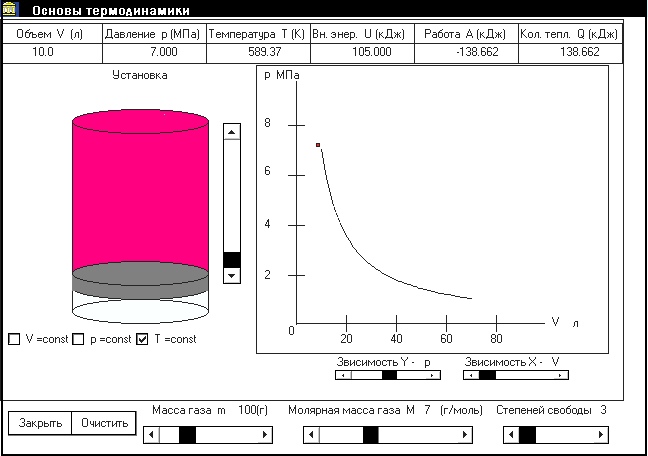
Рис.2. Рабочее окно программы

Таблица 1