1 .Гармонические колебания пружинного маятника

Простейшим типом колебательного движения являются гармонические колебания, т.е. такие, которые происходят по закону синуса или косинуса.

Одной из важнейших механических систем, способных совершать подобное движение, является пружинный маят­ник. Он представляет собой некоторый груз массой т, за­крепленный на упругой пружине, с коэффициентом жестко­сти k. Колебания совершаются под действием упругих сил, поэтому по закону Ньютона

а = F/m = - kх/т,

но так как ускорение – вторая производная смещения по времени а = , следовательно,

, или

Решением данного дифференциального уравнения явля­ется выражение

,

где х – смещение груза от положения равновесия;

А – максимальное значение колеблющейся величины (амплитуда);

– фаза колебания; – начальная фаза колебания;

– циклическая частота колебаний.

Используя связь между периодом колебаний и цикличе­ской частотой, окончательно для периода колебаний пру­жинного маятника получаем

(1)

С другой стороны, период можно найти по приведен­ному графику колебаний. Для этого по шкале времени не­обходимо определить время t, за которое происходит не­сколько колебаний. Так как период определяет время одного колебания, то он вычисляется по формуле

T = t/N, (2)

где N – число колебаний.

2. Свободные колебания маятника

Свободными называются колебания, которые проис­ходят за счет энергии, полученной телом в момент начала колебания. В реальных условиях эта энергия расходуется на преодоление сил сопротивления, что приводит к постепен­ному уменьшению амплитуды, т.е. ко­лебания становятся затухающими (рис.1). В большинстве случаев силы сопротивления про­порциональны ско­рости колеблюще­гося объекта :

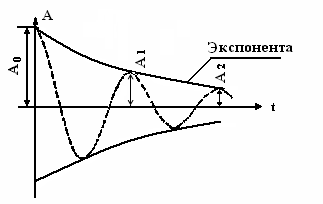
Рис.1. Свободные колебания

где r – коэффициент сопротивления среды.

Дифференциальное уравнение колебательного движе­ния с учетом данной силы примет вид

где α – коэффициент затухания колебаний, определяемый по формуле

α= r/2m. (3)

Решение данного уравнения имеет вид

где A(t) = – амплитуда затухающих колебаний, зависящая от времени;

– циклическая частота затухающих колебаний.

Тогда период

. (4)

Из полученных выражений видно, что коэффициент за­тухания определяет быстроту уменьшения амплитуды. Он является величиной, обратной промежутку вре­мени, за которое амплитуда убы­вает в е раз.

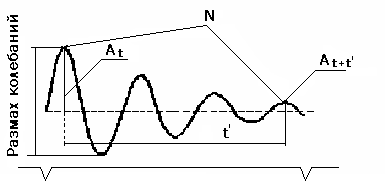
Рис. 2. Виброграмма колебаний

Другим важ­ным параметром затухающего колебания является логарифмический декремент затухания λ, равный логарифму отношения двух амплитуд, разделенных отрезком времени в один период Т:

(5)

Логарифмический декремент затухания – физическая величина, обратная числу колебаний, по истечении которых амплитуда убывает в е раз.

Для экспериментального определения коэффициента затухания необходимо определить амплитуды, соответст­вующие двум моментам времени t и t+t' (рис. 2). Тогда по определению коэффициента затухания

отсюда (6)

Зная же коэффициент затухания и период колеба­ний, декремент затухания можно найти с помощью выра­жения (5).