Задание к лабораторной работе

Упражнение 1. Движение частиц в электрическом поле

В качестве источника электрического поля в данной программе используется плоский конденсатор, создающий однородное электрическое поле с на­пряженностью Е. При этом положительно заряженная частица, пролетающая в данном поле, будет откло­няться по направлению поля (отрицательная – против на­правления поля) (рис.3).

Рис.3. Движение частиц в электрическом поле

Так как время пролета частицы

,

то отклонение частицы по вертикали

.

Отсюда можно выразить силу, действующую на частицу:

. (4)

1. Выберите заряд и массу частицы, а также значение начальной скорости. Задайте значение напряженности поля конденсатора.

Рис.4. Рабочее окно программы

2. После завершения эксперимента программа выдает проекции траектории на оси координат (рис.4). Запишите характеристики траектории в табл. 1.

3. Рассчитайте по формуле (4) значение силы, действующей на частицу.

4. Изменяя напряженность поля конденсатора, иссле­дуйте зависимость силы, действующей на частицу, от на­пряженности электрического поля. Данные занесите в табл. 1.

Таблица 1

Результаты измерений

m,мг	q,Кл	υ,м/с	z, м	y, м	F, Н	E,В/м

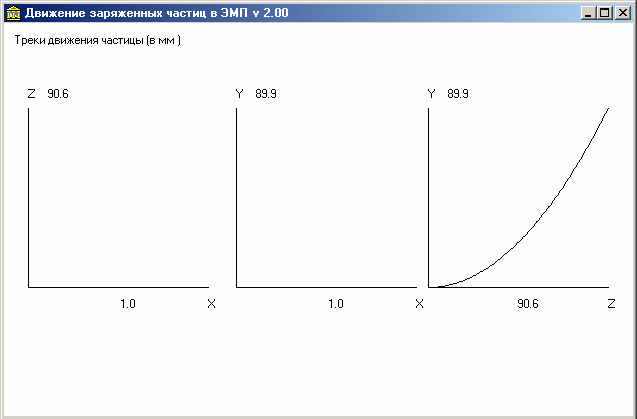
Рис.5. Проекция траектории движения

5. Изменяя заряд частицы, исследуйте зависимость силы, действующей на частицу от заряда. Данные занесите в табл. 2.

Таблица 2

Результаты измерений

m, мг	E, В/м	υ, м/с	z, м	y, м	F, Н	q, Кл

6. По данным табл. 1 и 2 постройте графики зависимо­стей F=f(E) и F=f(q).

7. Сделайте вывод о характере движения заряженной частицы в электрическом поле. В каких полях возможен данный тип движения?

Упражнение 2. Движение частиц в магнитном поле

Рис.6. Траектория движения в магнитном поле

1. Задайте некоторое значение индукции магнитного поля магнитов при отсутствии электрического поля конден­сатора. Рассмотрите траекторию движения частицы при трех различных положениях магнитов. Зарисуйте траекто­рии (рис.6). Пользуясь правилом левой руки, укажите на­правление силы Лоренца.

2. Изменяя величину индукции магнитного поля, иссле­дуйте зависимость силы, действующей на частицу от моду­ля вектора индукции. Так как центростремительное ускоре­ние частицы , то значение силы, действующей на частицу, можно вычислить по формуле . Диаметр окружности определяется из графика траектории движения. Результаты расчетов занесите в табл. 3.

Таблица 3