1. Методика аналізу стійкості за критеріэм Михайлова.

1. Знайдемо комплексний коефіцієнт передачі замкнутої системи 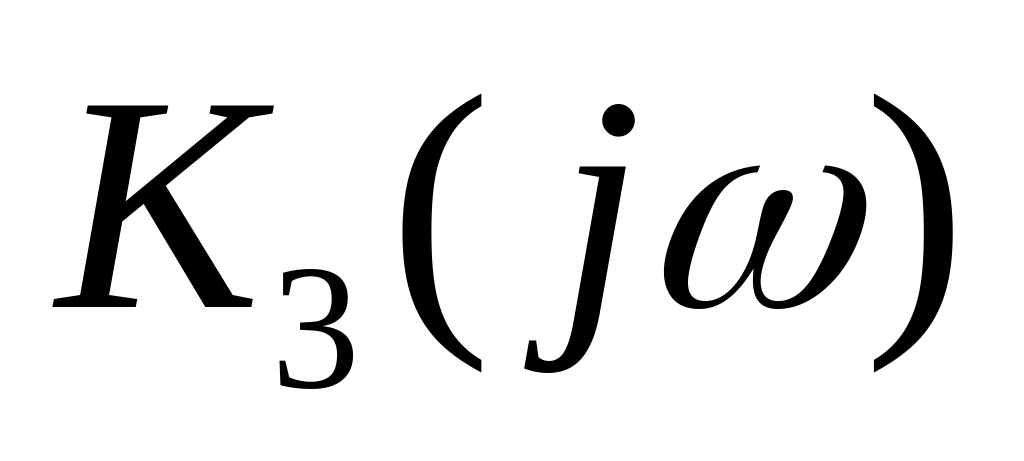і характеристичний поліном :

;

.

2. Визначимо критичні частоти 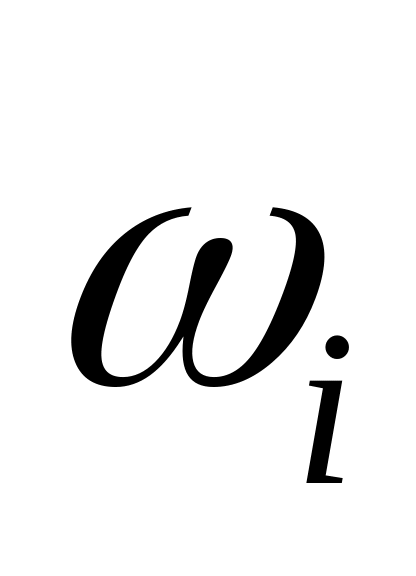, на яких годограф Михайлова перетинає|пересікає| дійсну вісь з|із| умови .

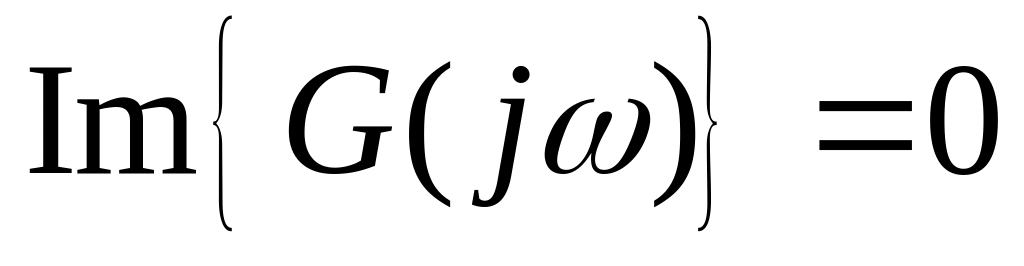3. Обчислимо|обчислятимемо| значення реальної частини|частки| на цих частотах і перевіримо чергування її знаків із|із| збільшенням частоти.

4. Визначимо частоти 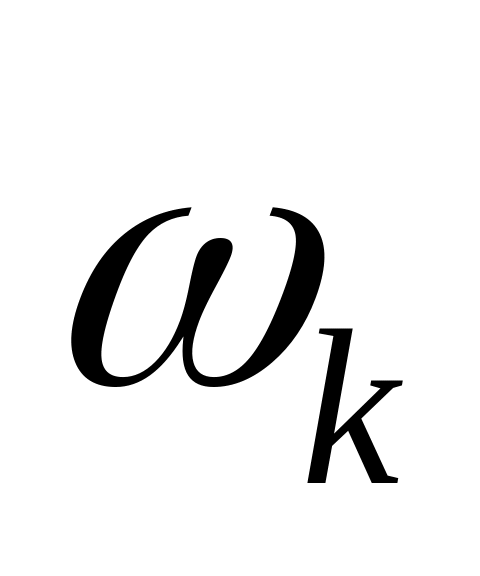, на яких годограф Михайлова перетинає|пересікає| уявну вісь з|із| умови .

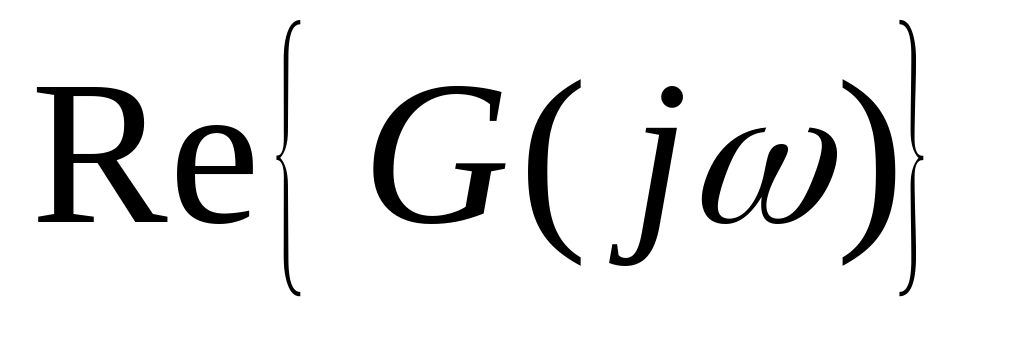5. Обчислимо|обчислятимемо| значення уявної частини|частки| на цих частотах 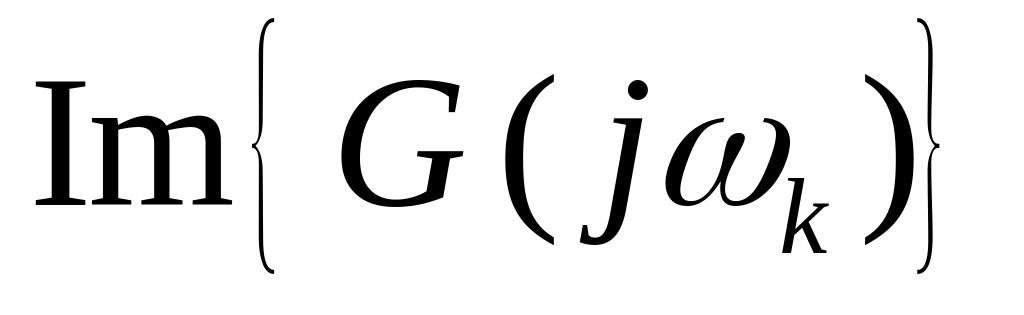і перевіримо чергування її знаків із|із| збільшенням частоти.

Якщо знаки значень і чергуються, то система стійка, якщо інакше – нестійка.

2. Методика визначення критичних частот і критичного коефіцієнта підсилення за критерієм Михайлова.

1. Визначимо критичні частоти 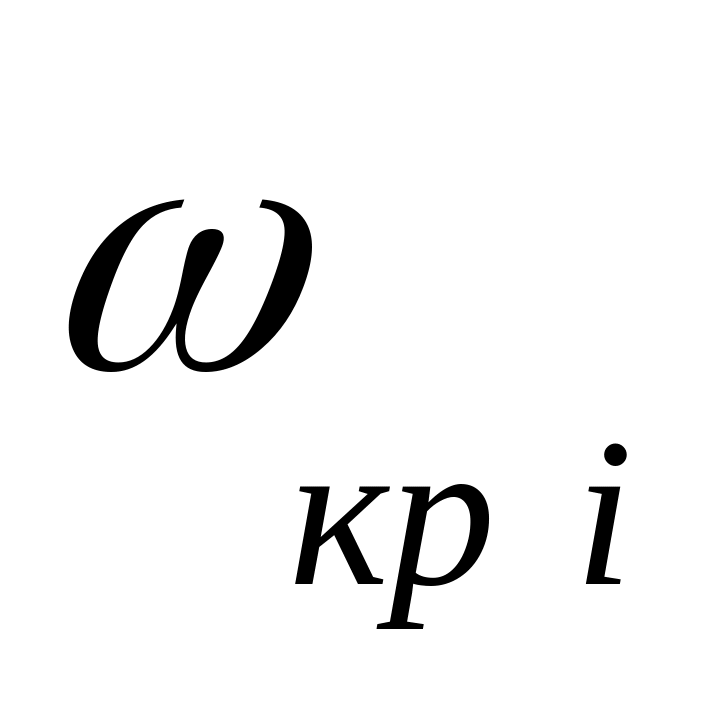з|із| умови .

2. Підставивши значення в , вирішимо|рішатимемо| рівняння 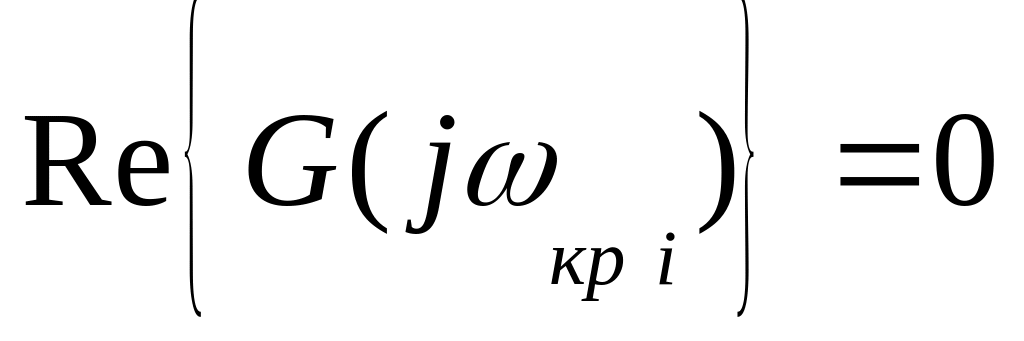та

отримаємо значення критичного коефіцієнта посилення .

3. Приклад|зразок| аналізу стійкості лінійної системи за критерієм Михайлова.

Дослідити стійкість і визначити критичні коефіцієнти підилення і критичні частоти замкненої системи, структурна схема якої показана на рис .1.2, для таких|таких| параметрів:

; ; ;

; ; ; ; ; ; .

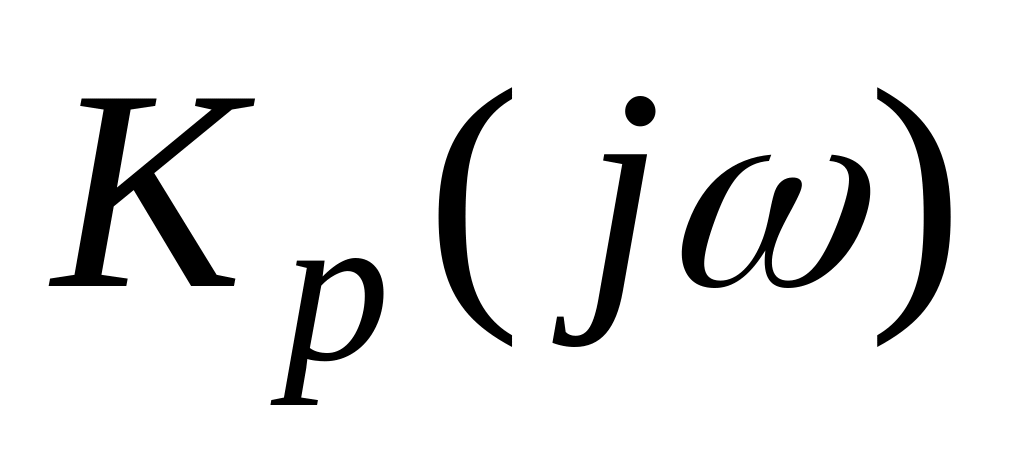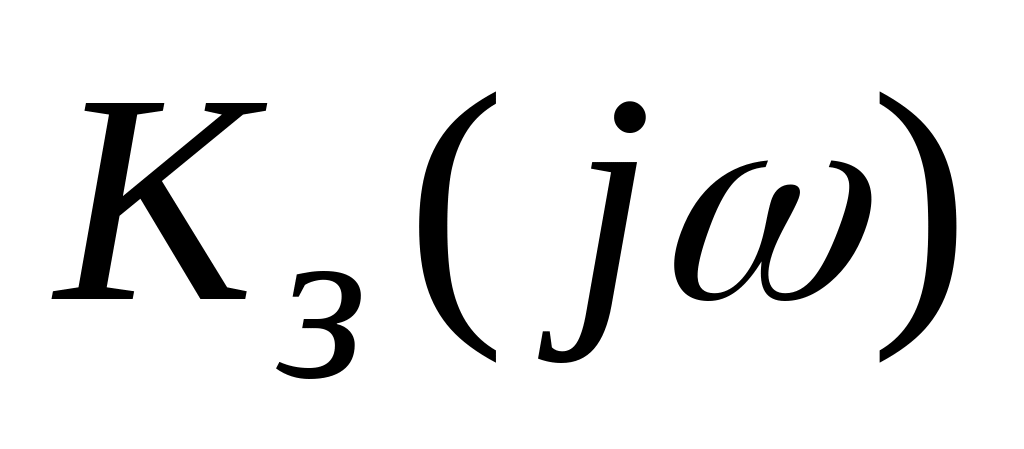1. Знайдемо комплексний коефіцієнт передачі розімкненої системи , замкненої системи і характеристичний поліном :

; ; ; ; .

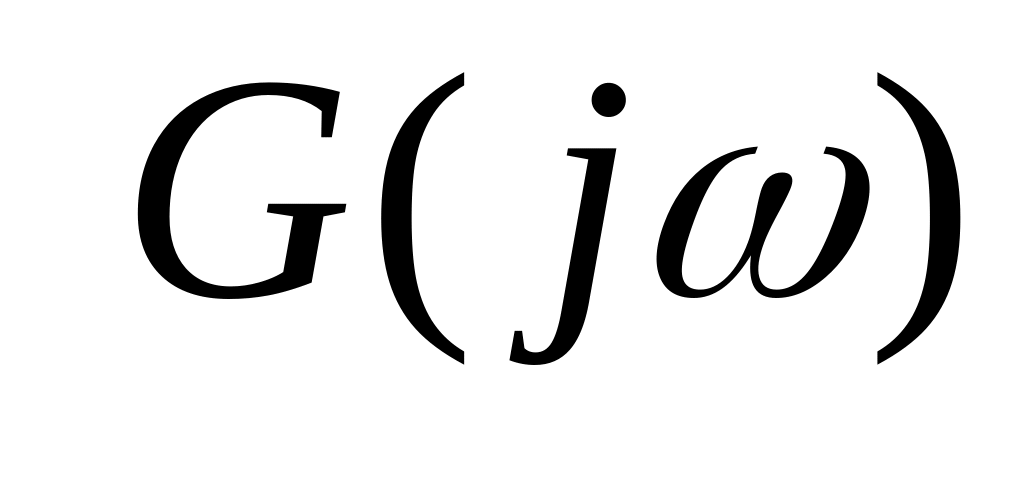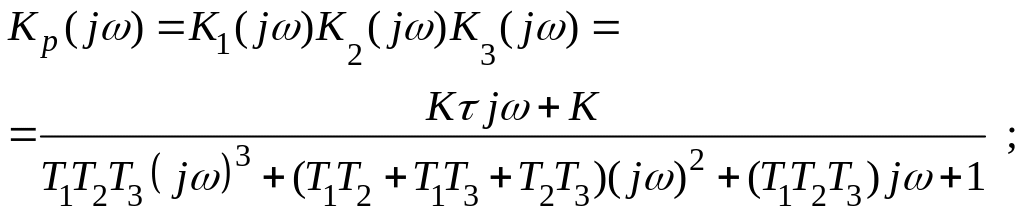
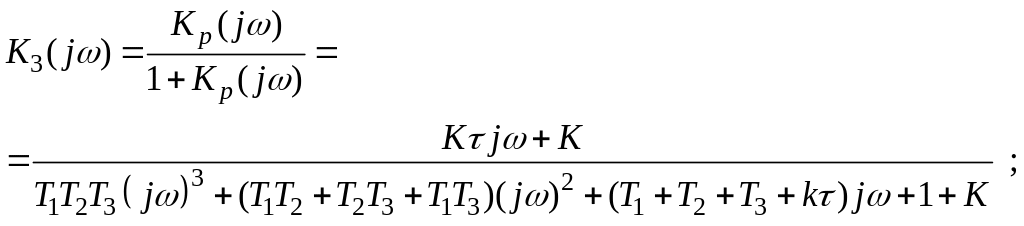
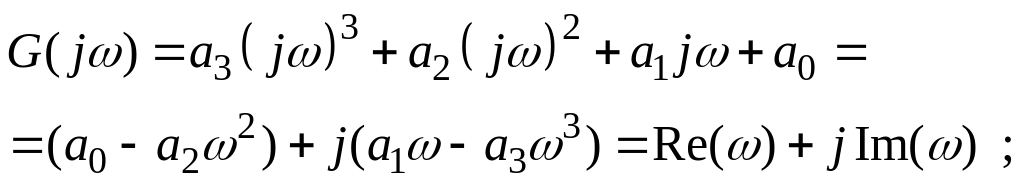
2. Визначимо критичні частоти 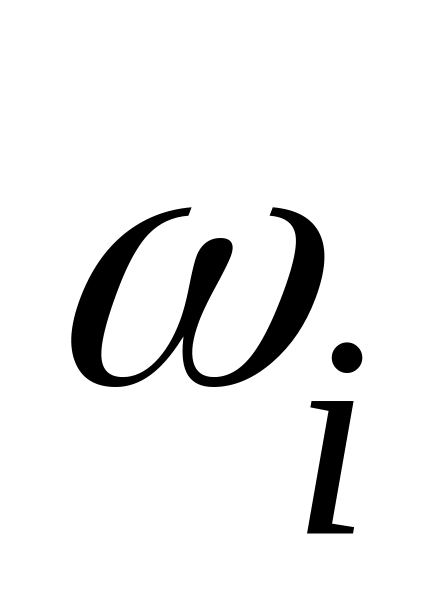, на яких годограф Михайлова перетинає|пересікає| дійсну вісь з|із| умови

;

; .

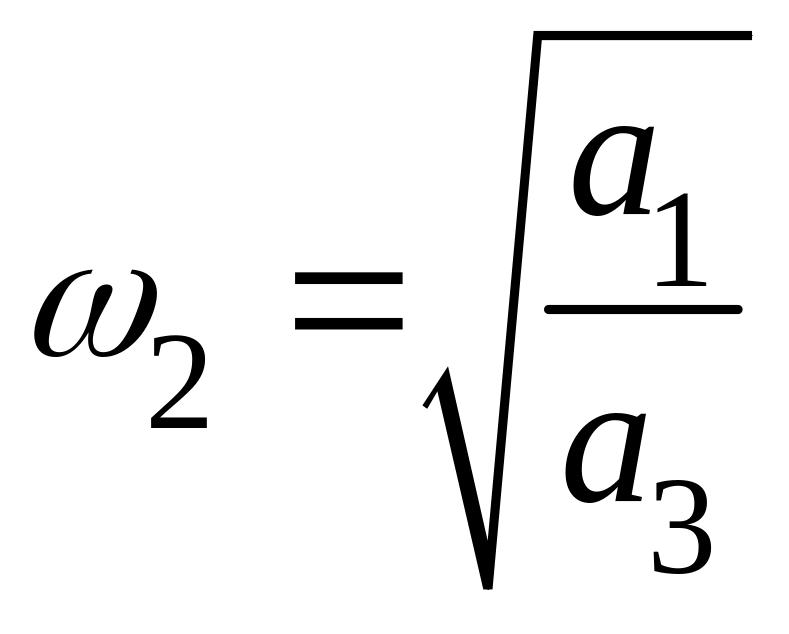3. Обчислимо|обчислятимемо| значення дійсної частини|частки| на цих частотах:

; .

4. Визначимо частоти 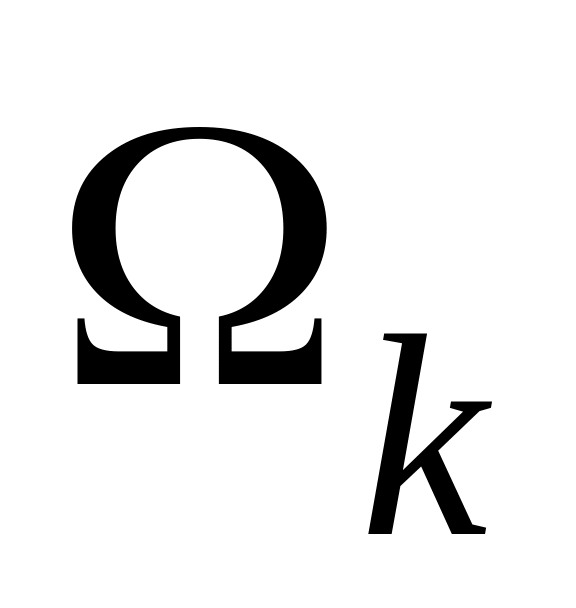, на яких годограф Михайлова перетинає|пересікає| уявну вісь з|із| умови :

.

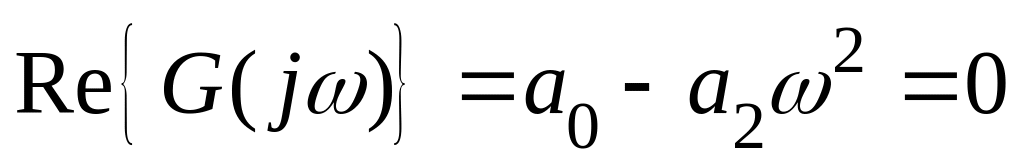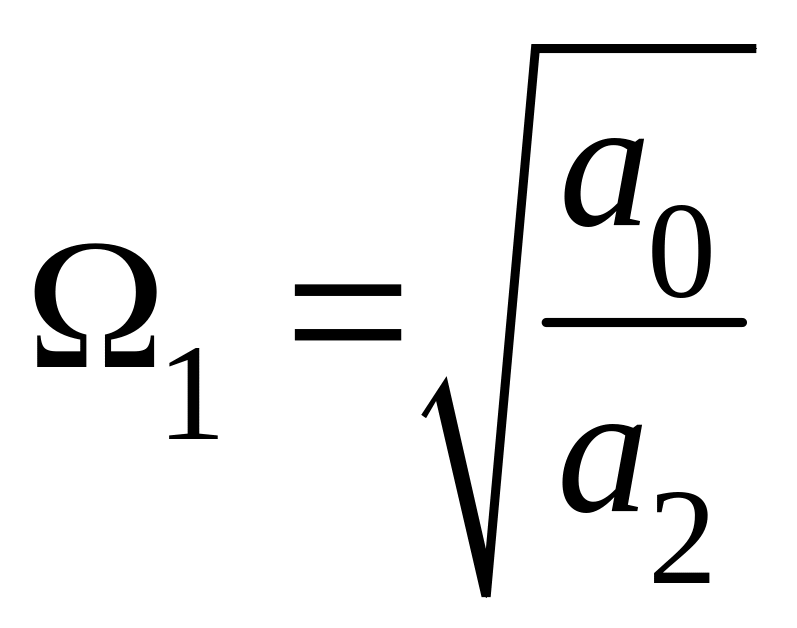5. Обчислимо|обчислятимемо| значення уявної частини|частки| на частоті :

.

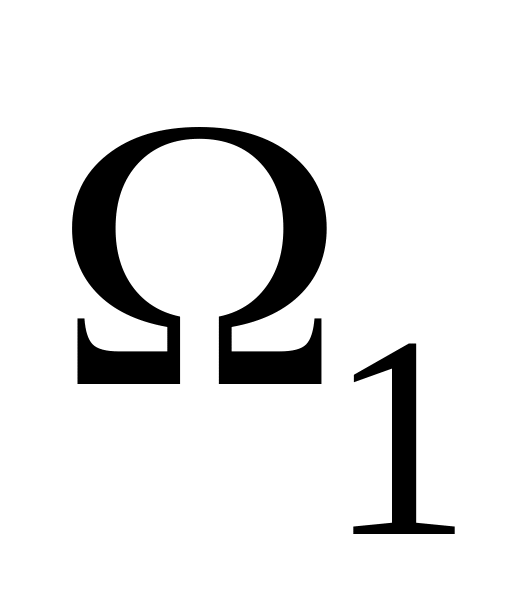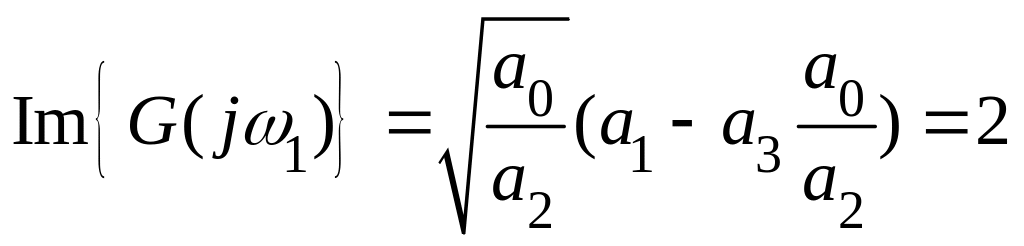оскільки|тому що| знаки реальної частини |частки| на частотах та чергуються, а уявна частина |частка| на частоті додатня, то система стійка.

6. Визначимо критичну частоту з|із| умови

;

.

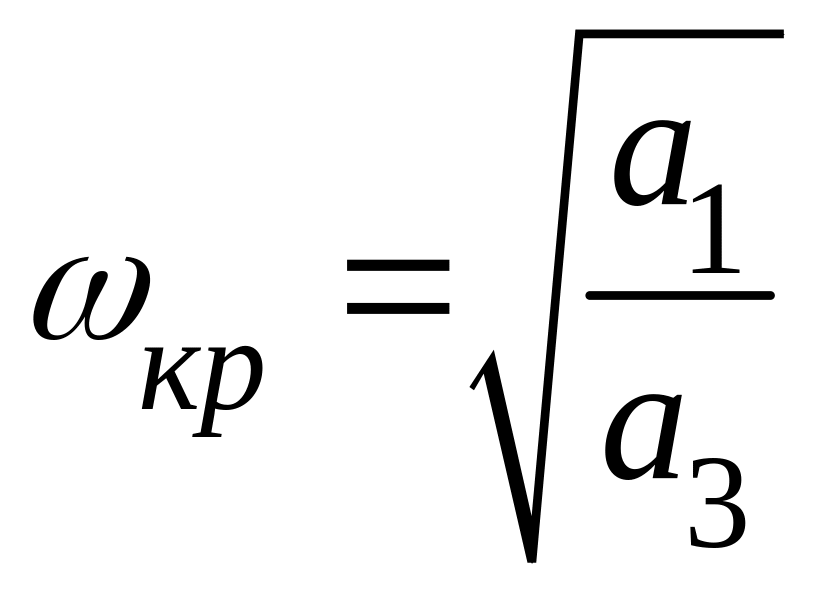7. Визначимо критичний коефіцієнт підсилення. Для цього підставимо значення 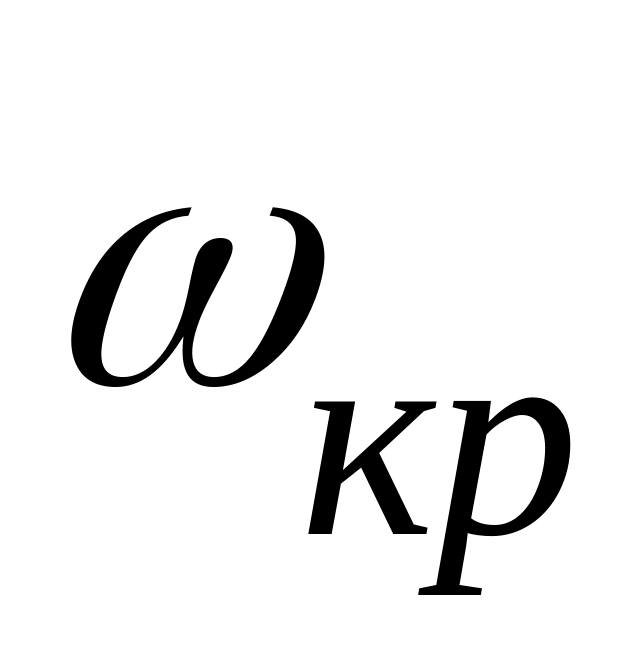в і вирішимо|рішатимемо| рівняння відносно K :

;

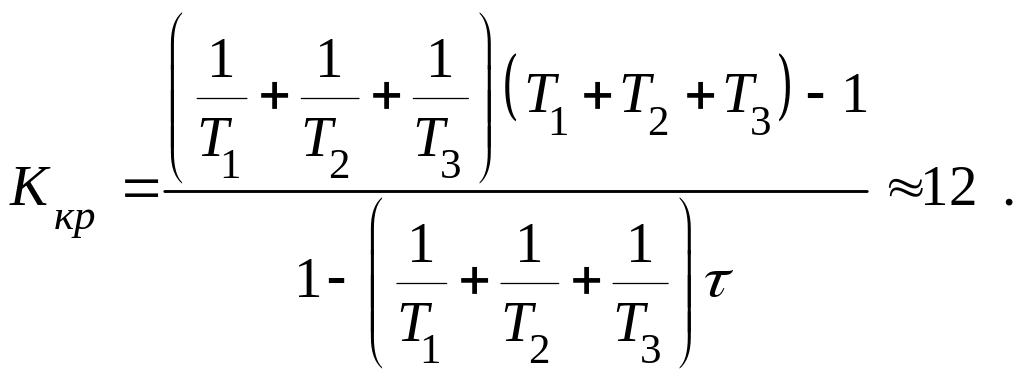
3. Критерій стійкості Найквіста.

Цей критерій дозволяє судити про стійкість замкнутої системи по вигляду|виду| амплітудно-фазової характеристики системи в розімкненому стані|достатку|. Приведемо два формулювання критерію Найквіста.

1. Якщо система в розімкненому стані|достатку| стійка, то для її стійкості в замкненому стані|достатку| необхідно і достатньо|досить|, щоб|аби| годограф вектора не охоплював точку з|із| координатами

2. Якщо система в розімкненому стані|достатку| нестійка і її характеристичний поліном має коренів в правій напівплощині, то для стійкості замкненої системи необхідно і достатньо|залишковий|, щоб|аби| годограф охоплював точку у додатньому напрямі|направленні| раз (різниця між числом переходів зверху вниз і знизу вверх на ділянці дійсної осі між та дорівнювала раз).

На рис.1.5 зображені|змальовувати| годографи систем, стійких як в розімкненому стані|достатку|, так і в замкненому, а на рис.1.6 зображений годограф системи, нестійкої в розімкненому стані|достатку| і стійкої в замкненому, характеристичне рівняння якої має два корені з|із| додатньою дійсною частиною|часткою|. Якщо амплітудно-фазова характеристика проходить через точку з|із| координатами , то система знаходиться|перебуватиме| на межі|кордоні| стійкості.

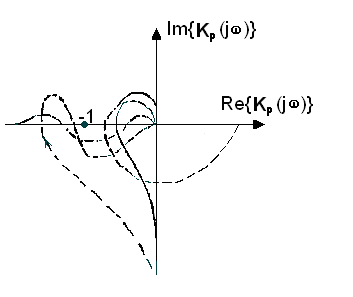
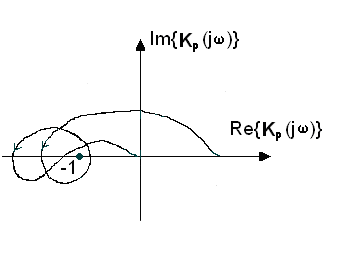
Рис.1.5 Рис. 1.6

Частота, при якій модуль , тобто амплітудно-частотна характеристика, дорівнює одиниці, називається частотою зрізу . Частота, при якій аргумент , тобто фазо-частотна характеристика, дорівнює , називається критичною частотою .

По годографу можна легко визначити запаси стійкості по амплітуді і фазі (Рис.1.7). Запас стійкості по амплітуді (посиленню) знаходиться|перебуває| на критичній частоті відповідно до виразу|вираження|

.

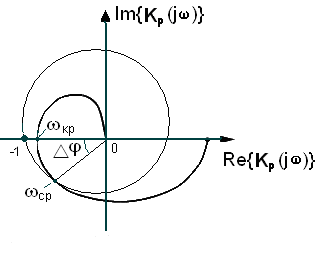
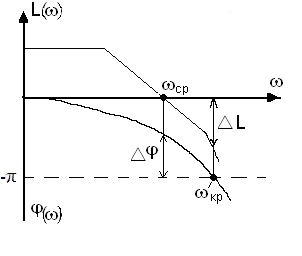
Рис.1.7 Рис. 1.8

Запас стійкості по фазі слід визначати на частоті зрізу, на якої коефіцієнт підсилення системи дорівнює 1 :

.

Скориставшись критерієм Найквіста, легко досліджувати стійкість лінійних систем по логарифмічним амплітудно-частотним (ЛАЧХ) і логарифмічним фазо-частотним|| (ЛФЧХ) характеристикам (рис 1.8).

У|біля| систем, стійких в розімкненому стані|достатку|, на частоті , при якій ЛАЧХ проходить через рівень 0дБ|нуль-індикатор|, ЛФЧХ не повинна досягати рівня , а на критичній частоті , при якій ЛФЧХ проходить|минає| через рівень , ЛАЧХ має бути від’ємною|заперечною|, тобто якщо , то система стійка.

Запас стійкості по підсиленню, виражений|виказувати| в децибелах, , і запас стійкості по фазі показаний на рис.1.8.