1. Методика визначення стійкості лінійної системи зао критерієм Гурвиця.

1. Знайдемо передаточну функцію розімкненої системи:

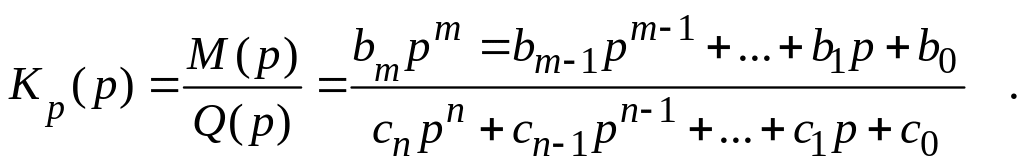
2. Визначимо передаточну функцію замкненої системи:

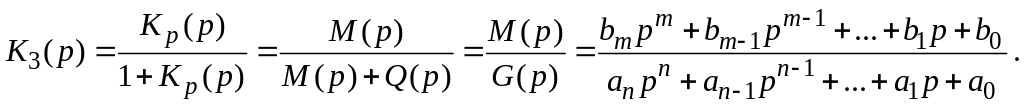
3. Запишемо характеристичний поліном замкненої системи:

.

4. Відповідно до (1.1) складемо матрицю Гурвиця.

5. Використовуючи (1.2), обчислимо|обчислятимемо| визначники Гурвиця.

6. Якщо 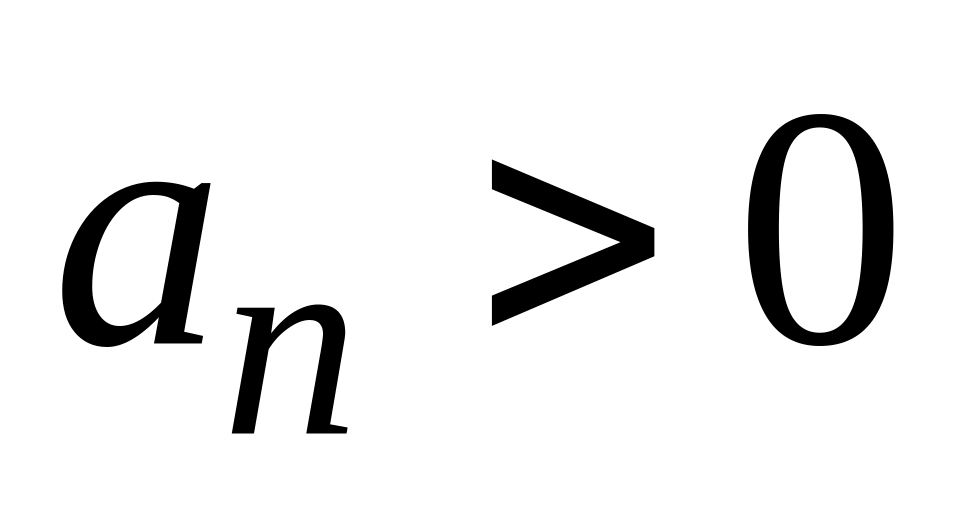, , 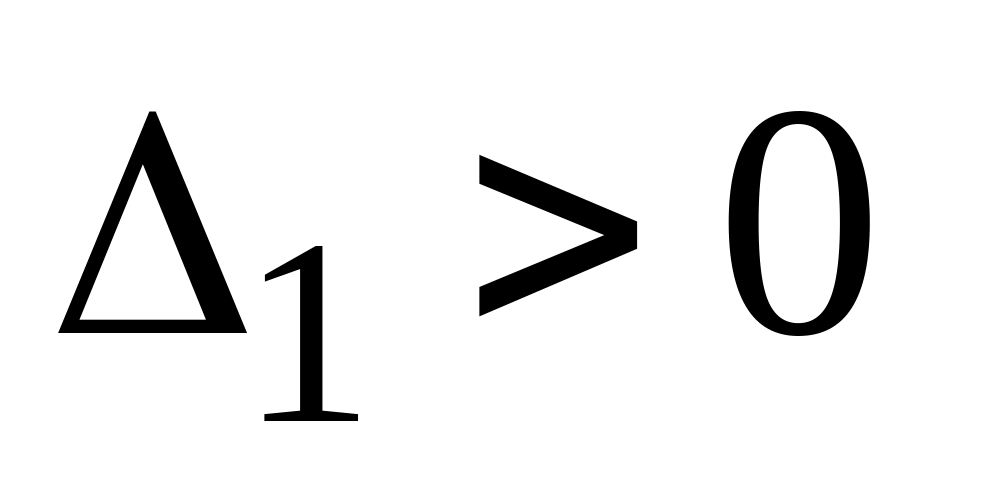, 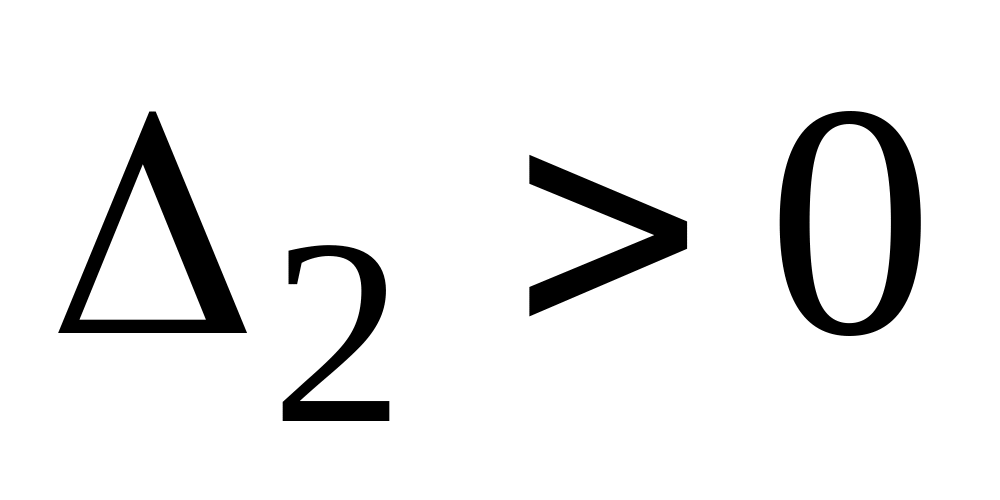… , , 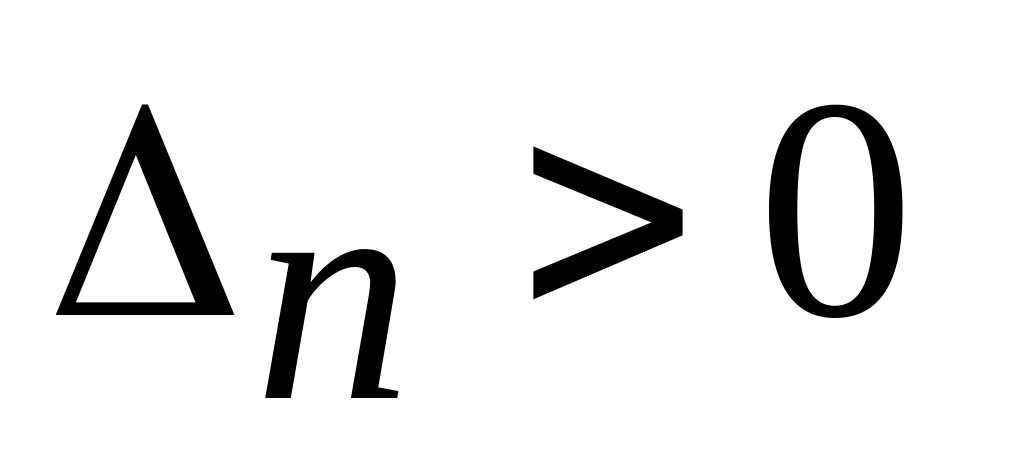то система стійка, якщо інакше – не стійка.

2. Методика визначення критичного коефіцієнта підсилення системи.

1-4. Повторити п.п.1-4 попередньої методики.

5. Обчислити|обчисляти| визначник Гурвиця максимального порядку|ладу| .

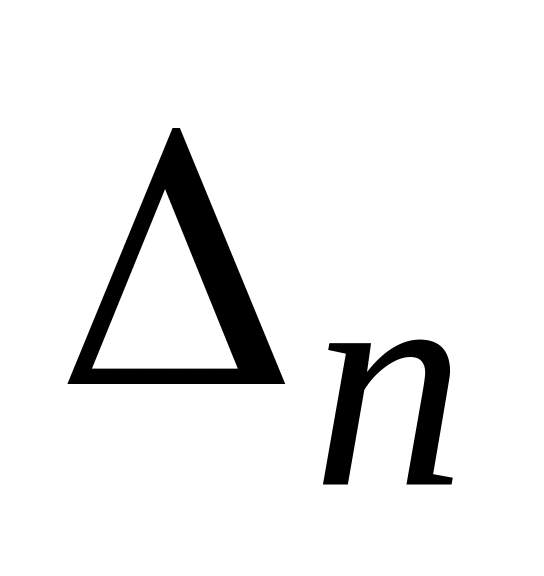6. Вирішити|рішати| рівняння 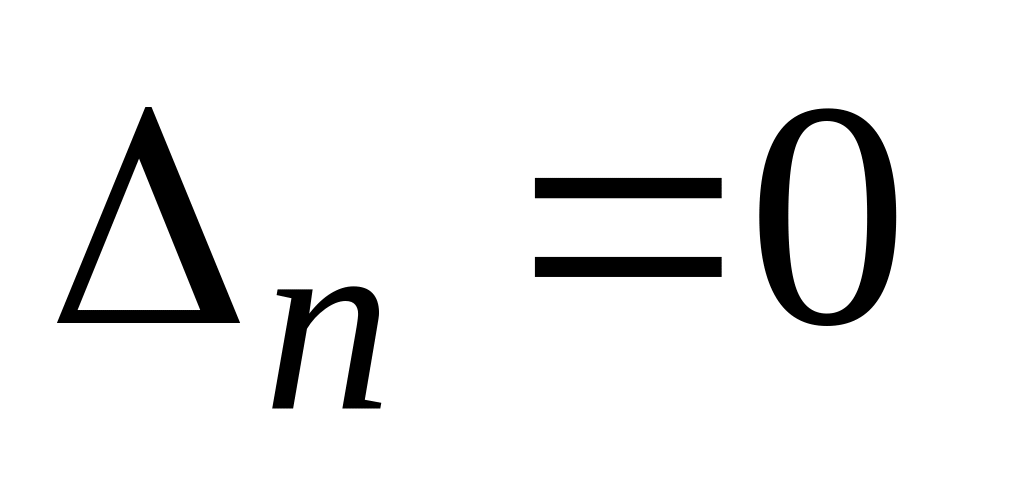відносно коефіцієнта підсилення системи. В результаті отримуємо значення критичного коефіцієнта підсилення .

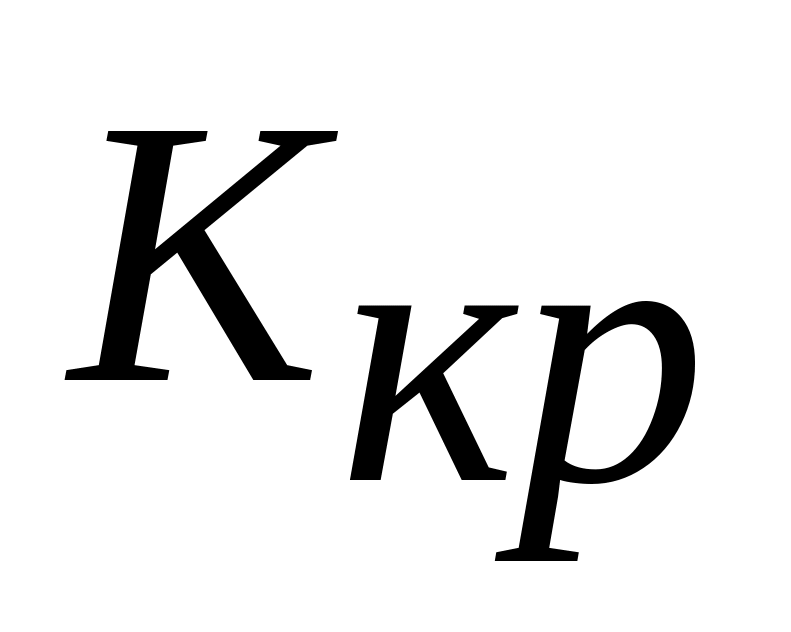3. Приклад аналізу стійкості лінійної системи за критерієм Гурвиця.

Дослідити стійкість і визначити критичний коефіцієнт підсилення замкненої системи, структурна схема якої показана на рис.1.2, для таких|таких| параметрів:

; ; ;

; ; ; ; ; .

2. Знайдемо передаточну функцію розімкненої системи:

; .

3. Визначимо передаточну функцію замкненої системи:

.

4. Запишемо характеристичний поліном замкненої системи:

.

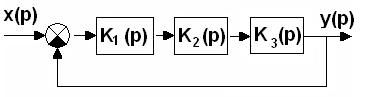
Рис.1.2

5. Складемо матрицю Гурвиця:

.

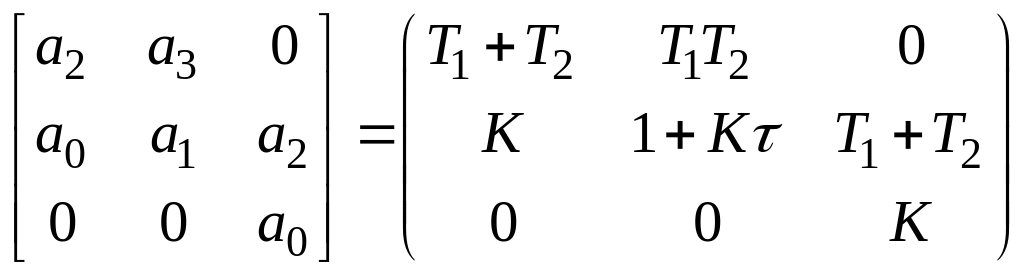6. Обчислимо|обчислятимемо| визначники Гурвиця:

, ;

.

7. З|із| умови 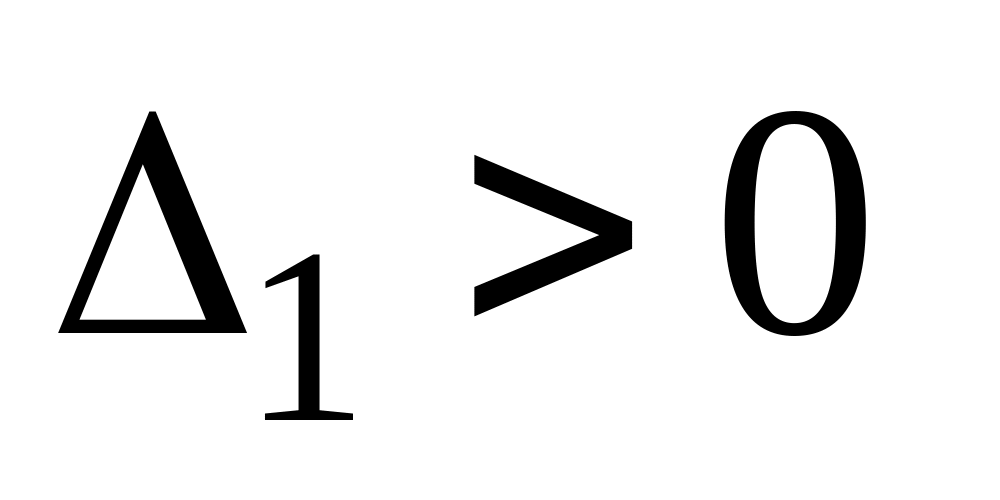, , 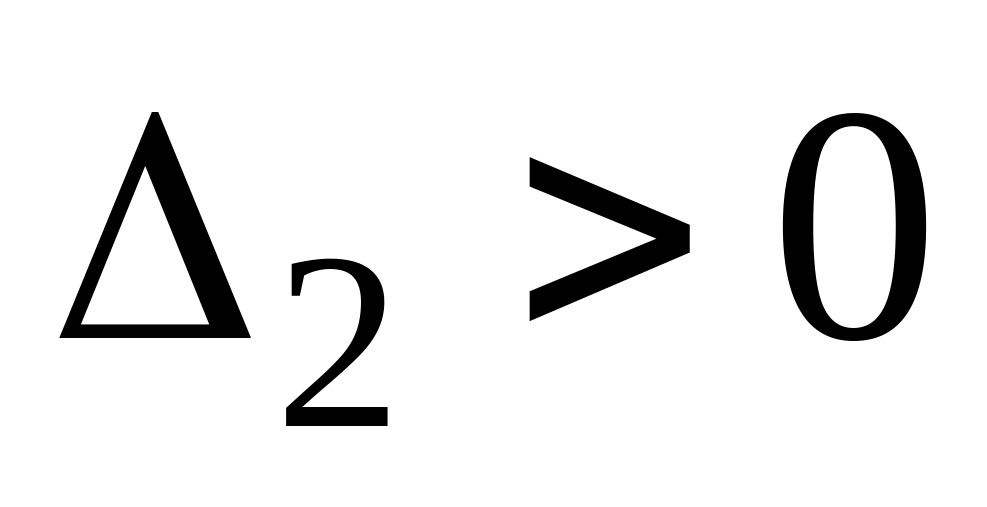, 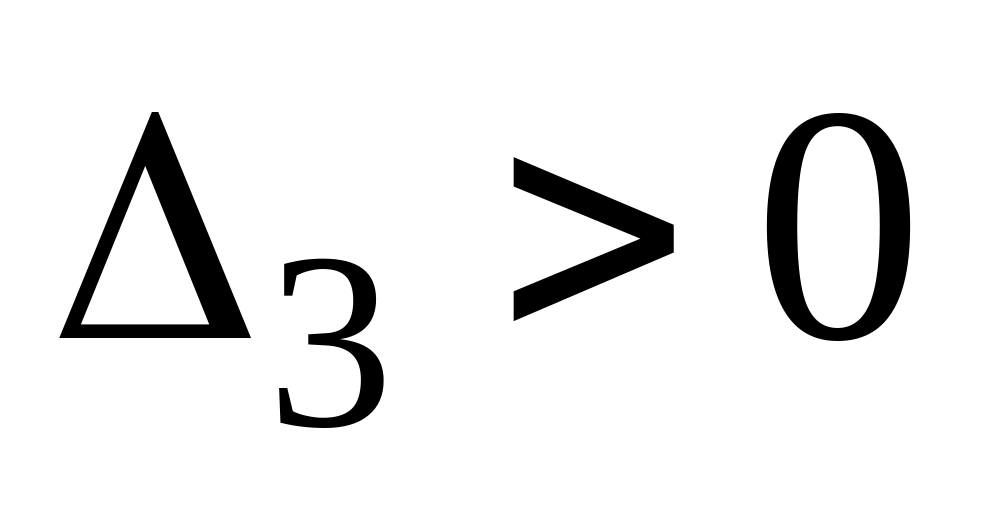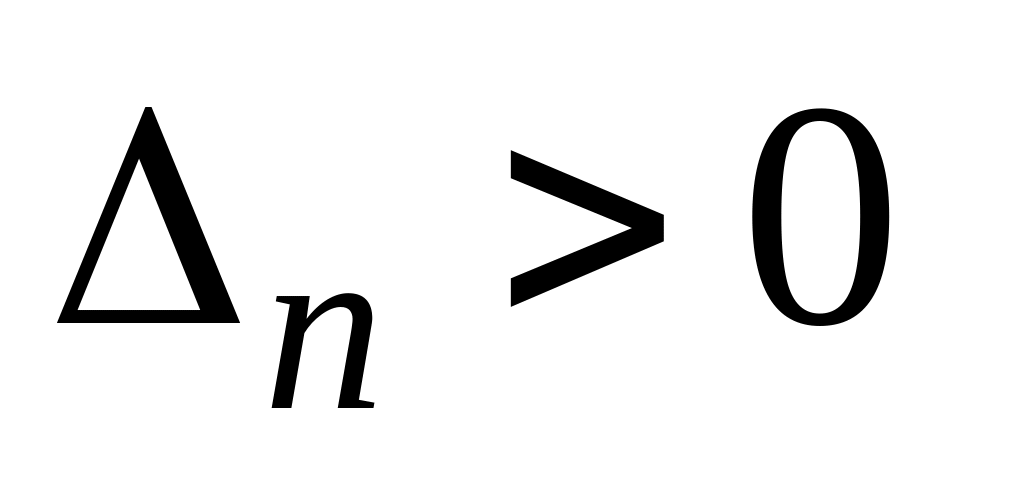знайдемо

.

Отже, при система стійка за умови , а при за умови .

Підставивши значення параметрів , , , ,

, , отримаємо|одержуватимемо|, тобто система стійка.

8. Визначимо критичний коефіцієнт підсилення з|із| рівняння

, звідси

2. Критерій стійкості Михайлова.

Для стійкості системи по Михайлову необхідно і достатньо|досить|, щоб|аби| при зміні частоти від нуля|нуль-індикатора| до нескінченості приріст аргументу вектора характеристичного полінома (знаменника комплексного коефіцієнта передачі замкненої) системи був рівний , де - порядок|лад| характеристичного полінома [3;4]:

; .

При аналізі стійкості системи за допомогою критерія Михайлова у вираз|вираження| для або та підставляють значення і будують годограф Михайлова, який по черзі перетинатиме|пересікатиме| то уявну вісь, то дійсну. Причому для стійкості системи знаки значень та в точках перетинів|пересічень| з|із| осями повинні чергуватися.

На рис.1.3 показані годографи стійких систем, а на рис.1.4 – нестійкої системи.

Якщо годограф вектора пройде через початок координат то система знаходиться|перебуває| на межі|кордоні| стійкості. При цьому з|із| умови визначаються критичні частоти , а з|із| умови - критичний коефіцієнт підсилення.

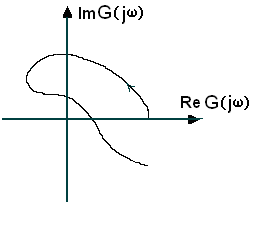
Рис.1.3 Рис. 1.4

1.2.1